算法稳定性:不稳定
复杂度分析:
- 空间复杂度:O(1)
- 时间复杂度:O(n*logn)
实现代码:
#include<iostream>
using namespace std;
void HeapAdjust(int *nums,int x,int n) {
nums[0] = nums[x];
for (int i = 2 * x;i <= n;i *= 2) {
if (i < n && nums[i] < nums[i + 1])
i++;
if (nums[0] >= nums[i]) {
break;
}else {
nums[x] = nums[i];
x = i;
}
}
nums[x] = nums[0];
}
void BuildMaxHeap(int* nums, int n) {
for (int i = n / 2;i >= 1;i--) {
HeapAdjust(nums, i, n);
}
}
void HeapSort(int* nums, int n) {
BuildMaxHeap(nums, n);
for (int i = n;i > 1;i--) {
swap(nums[1], nums[i]);
HeapAdjust(nums, 1, i-1);
}
}
int main() {
int nums[155];
int n;
cin >> n;
for (int i = 1;i <= n;i++)
cin >> nums[i];
HeapSort(nums, n);
cout << "排序后序列为:";
for (int i = 1;i <= n;i++)
cout << nums[i] << " ";
return 0;
}
运行结果:
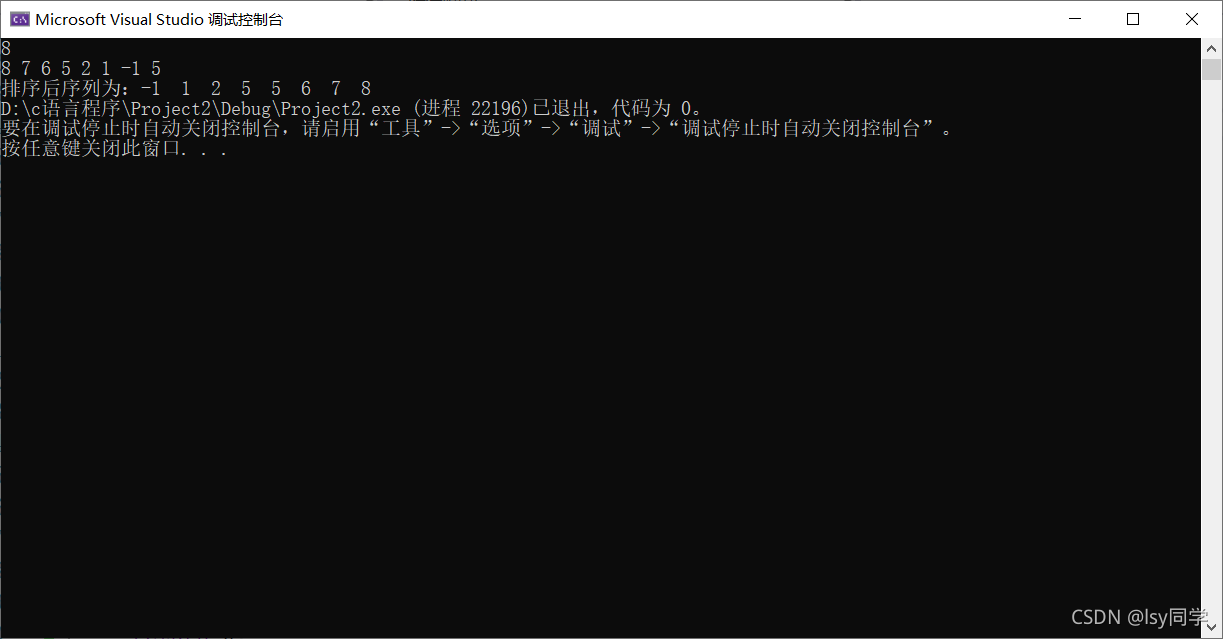








 本文介绍了堆排序算法的稳定性及复杂度分析,空间复杂度为O(1),时间复杂度为O(n*logn)。通过大根堆实现从小到大的排序。提供了完整的C++实现代码,包括HeapAdjust、BuildMaxHeap和HeapSort三个关键函数。运行结果显示了排序后的序列。
本文介绍了堆排序算法的稳定性及复杂度分析,空间复杂度为O(1),时间复杂度为O(n*logn)。通过大根堆实现从小到大的排序。提供了完整的C++实现代码,包括HeapAdjust、BuildMaxHeap和HeapSort三个关键函数。运行结果显示了排序后的序列。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








