类似斐波那契数列：奶牛生牛问题：奶牛生下来3年可以成熟生小牛，请问第N年一共多少牛

类似斐波那契数列：奶牛生牛问题：奶牛生下来3年可以成熟生小牛，请问第N年一共多少牛？

有了斐波那契数列，其实经常又大厂会改编一些类似斐波那契数列的题目来考，因此，这类题目咱们要总结和梳理一下，以防万一
提示：矩阵A的p次幂的快速乘法，是重要的优化算法基础知识

之前的基础：咱们求过数字最快速乘幂的方法（数字a的p次幂），
（1）最快乘法：普通数字a的p次幂怎么求速度最快，不用Math.pow(a,p)哦
（2）咱们求过矩阵最快速乘幂的方法（矩阵A的p次幂），
最快矩阵乘法：矩阵A的p次幂怎么求速度最快，Math根本没有求矩阵的幂次函数

这俩知识点，你必须看懂，否则这个文章你看不懂！
这俩知识点，你必须看懂，否则这个文章你看不懂！
这俩知识点，你必须看懂，否则这个文章你看不懂！

在笔试中，建议还是用暴力递归改记忆化搜索算法，或者改动态规划填表的做法！
笔试的话，不建议用快速矩阵乘法来求斐波那契数列类似的问题！

但是在，面试的过程中，先可以用暴力递归解决类似的问题，改动态规划
然后，咱们可以秀一下自己的优化实力与技能！即完全可以用矩阵的乘幂来求类似的斐波那契数列f(n)题
下列文章是重要的关于斐波那契数列的题目：
（3）斐波那契数列：暴力递归改动态规划
（4）用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快

---

题目

类似斐波那契数列：奶牛生牛问题：
第1年，有一头奶牛A，总牛数为1；
第2年，A它生下一头奶牛B，总牛数为2；3年后，B可以成熟然后生小牛1头；
第3年，A它生下一头奶牛C，总牛数为3；3年后，C可以成熟然后生小牛1头；
第4年，A它生下一头奶牛D，总牛数为4；3年后，D可以成熟然后生小牛1头；
第5年，A它生下一头奶牛E，同时，B成熟了，B也生下一头奶牛F，总牛数6；
请问第N年一共有多少奶牛？【从不考虑公牛的事情】

额外一个题：上面的情况再加，奶牛5年就死亡，那第n年又有多少牛？

---

一、审题

示例：细心观察找递归公式
第1年，有一头奶牛A，总牛数为f(1)=1；
第2年，A它生下一头奶牛B，总牛数为f(2)=2；3年后，B可以成熟然后生小牛1头；
第3年，A它生下一头奶牛C，总牛数为f(3)=3；3年后，C可以成熟然后生小牛1头；
第4年，A它生下一头奶牛D，总牛数为f(4)=4；3年后，D可以成熟然后生小牛1头；
第5年，A它生下一头奶牛E，同时，B成熟了，B也生下一头奶牛F，总牛数f(5)=6；
第6年，A它生下一头奶牛G，同时，B也生下一头奶牛H，C成熟了，生下一头奶牛I，总牛数f(6)=9；
其实，不就是在第5年的情况下，多增加f(n-3)吗？你看看是不是？
f(6)=f(5)+f(3)=6+3=9;
f(5)=f(4)+f(2)=4+2=6;
f(n)=f(n-1)+f(n-3)

---

二、暴力递归公式已经通过观察得知

f(n)=f(n-1)+f(n-3)
其中，f(1）=1；f(2）=2；f(3）=3；

显然，类似于斐波那契数列一样，都是这种系列的。
（3）斐波那契数列：暴力递归改动态规划

自然，咱们就可以写一个暴力递归，然后改记忆化搜搜，顺便改写动态规划的转移方程填写dp表，这都是顺理成章的事情：

暴力递归代码：

有暴力递归递推公式才是关键，手撕代码不是问题！

//复习奶牛问题：
    //f(n)=f(n-1)+f(n-3)
    //其中，f(1）=1；f(2）=2；f(3）=3；
    public static int fNaiNiu(int n){
        if (n == 1) return 1;
        if (n == 2) return 2;
        if (n == 3) return 3;

        return fNaiNiu(n - 1) + fNaiNiu(n - 3);
    }


    public static void test(){
        System.out.println(feiBoCow(6));
        System.out.println(fNaiNiu(6));
    }

    public static void main(String[] args) {
        test();
    }

9
9

笔试AC解：改记忆化搜索代码，dp傻缓存跟随暴力递归

有暴力递归代码才是关键，改傻缓存和转移方程都非常简单

 //复习奶牛问题：
    //f(n)=f(n-1)+f(n-3)
    //其中，f(1）=1；f(2）=2；f(3）=3；
    public static int fNaiNiuDP(int n, int[] dp){
        if (dp[n] != -1) return dp[n];

        if (n == 1) {
            dp[n] = 1;
            return dp[n];
        }
        if (n == 2) {
            dp[n] = 2;
            return dp[n];
        }
        if (n == 3) {
            dp[n] = 3;
            return dp[n];
        }

        dp[n] = fNaiNiuDP(n - 1, dp) + fNaiNiuDP(n - 3, dp);

        return dp[n];
    }
    public static int fNaiNiuDP(int n){
        if (n < 1) return 0;

        int[] dp = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            dp[i] = -1;//初始化
        }

        return fNaiNiuDP(n, dp);
    }

    public static void test(){
        System.out.println(feiBoCow(6));
        System.out.println(fNaiNiu(6));
        System.out.println(fNaiNiuDP(6));
    }

    public static void main(String[] args) {
        test();
    }

9
9
9

面试精华解：改动态规划转移方程，填写dp表

//面试精华解：改动态规划转移方程，填写dp表
    public static int fNaiNiuDP2(int n){
        if (n < 1) return 0;

        int[] dp = new int[n + 1];
        //从左往右
        //根据暴力递归改
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;

        for (int i = 4; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 3];//转移方程--根据暴力递归改来的，面试就用这很好
        }

        return dp[n];
    }

    public static void test(){
        System.out.println(feiBoCow(6));
        System.out.println(fNaiNiu(6));
        System.out.println(fNaiNiuDP(6));
        System.out.println(fNaiNiuDP2(6));
    }

    public static void main(String[] args) {
        test();
    }

9
9
9
9

重磅优化技能：快速矩阵幂次法求类似斐波那契数列问题

类似斐波那契数列的定义：

咱们知道斐波那契数列是f(n)=f(n-1)+f(n-2)
当时有一个特别奇特的矩阵幂次求解法：
（4）用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快

那说到了斐波那契数列的矩阵理论是：

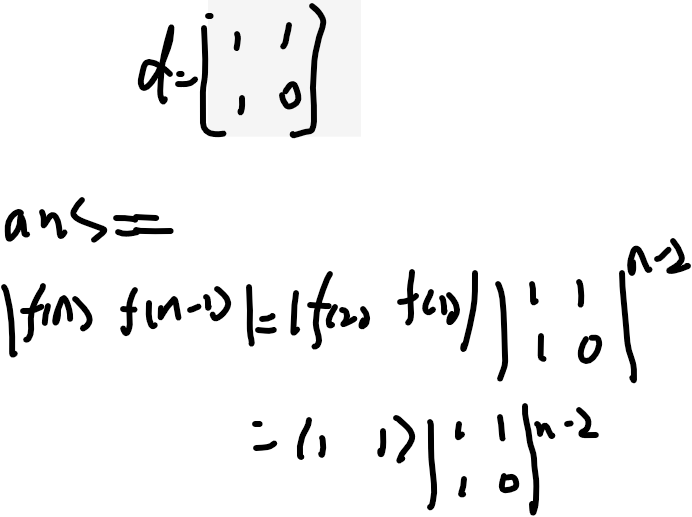
刚刚看到了奶牛生牛问题，牛杂第n年的总数是f(n)=f(n-1)+f(n-3)

这两者好生相似的

今天，咱们就来简介一个更普遍的类似斐波那契数列问题的理论定义：
f(n)=c1f(n-1)+c2f(n-2)+…+ck*f(n-k)
类似斐波那契数列一样，它也有矩阵幂次表达式，你也要熟悉：
f(n),f(n-1),…,f(n-k+1)=f(k),f(k-1),…,f(1)×d的n-k次幂
ck可以从0–无穷，随意取值
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！
f(n)就称为类似斐波那契数列问题的定义递推公式，这个公式横行天下！！！有大量的互联网大厂们会改编这个公式来出题！！！

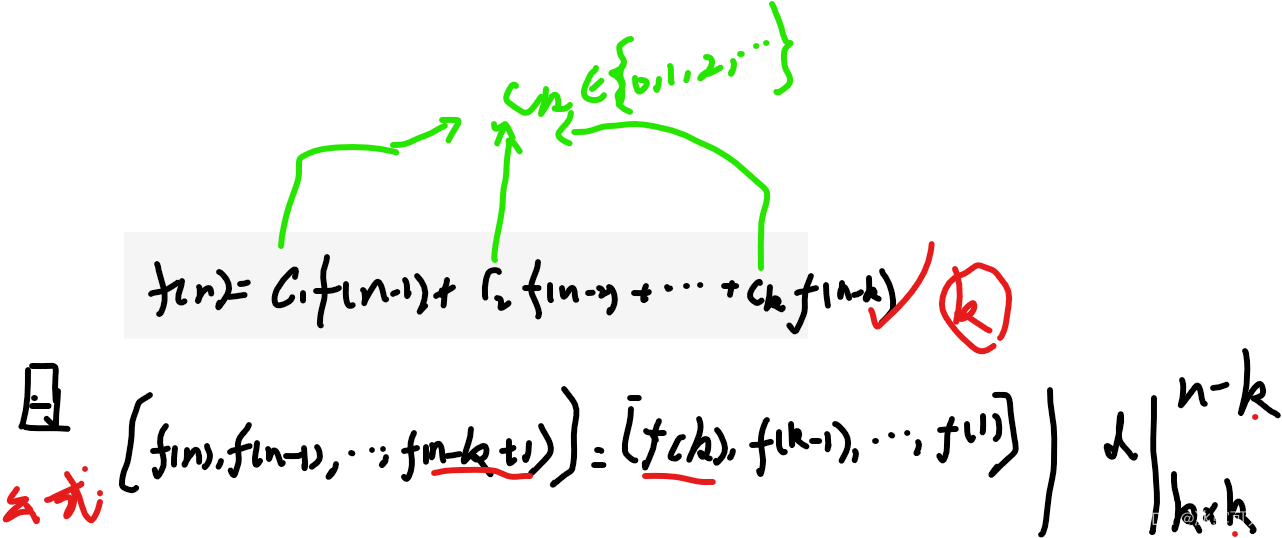
而且，这个公式有一个和斐波那契数列那个公式的矩阵幂次理论一样，也有一个可以用矩阵求幂次的方法来解f(n)，
只不过d不同罢了，因k不同而已，自己可以利用初始化的方式，求出d来。

本题，自然，c1=1,c3=1,其余ck=0
就是一个类似斐波那契数列改编来的牛奶生牛问题！

故完全可以像这样做：
（4）用矩阵乘幂的方法，求斐波那契数列f(n)=f(n-1)+f(n-2)，不用递归求，速度非常非常快

咱就去推它d咋来的，无非就是繁琐了点

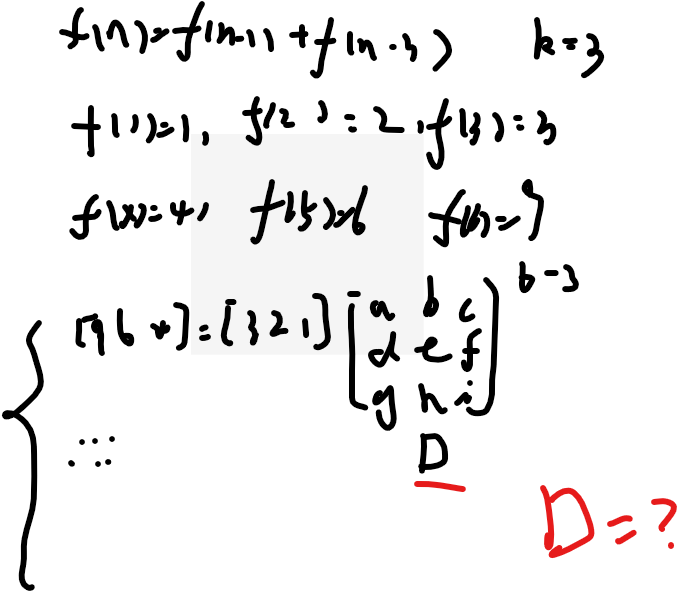
对于奶牛问题，记住d矩阵就是：

显然，f(n)的矩阵表达就出来了：f(n),f(n-1),f(n-2) = 3 2 1 × d的n-3次幂

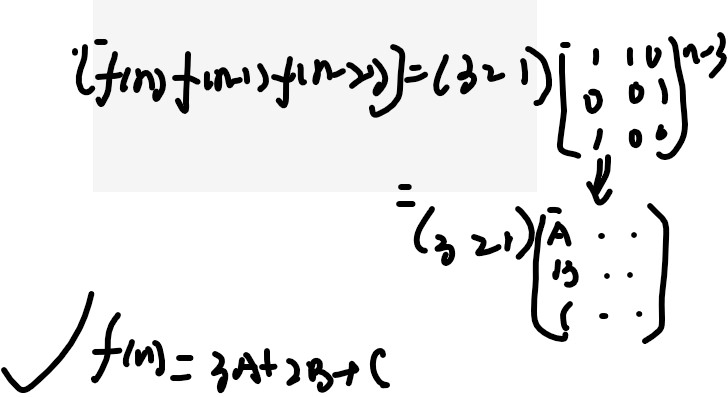
重要的就是求d的n-3次幂了

这也就是咱们之前的重要矩阵A的p次幂的快速算法问题了，可以直接用他们的代码：

//超级优化

    //复习斐波那契数列
    //最快矩阵乘法：矩阵A的p次幂怎么求速度最快，Math根本没有求矩阵的幂次函数

    //C=A×B咋求
    public static int[][] matrixMul(int[][] A, int[][] B){
        int m = A.length;
        int b = B[0].length;
        int[][] C = new int[m][b];//A的一行，×B的一列，求和，放在C的m行，b列

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < b; j++) {
                //A的一行，×B的一列，求和，放在C的m行，b列
                int ans = 0;
                for (int k = 0; k < A[0].length; k++) {//是A的列哦
                    ans += A[i][k] * B[k][j];
                }
                C[i][j] = ans;
            }
        }

        return C;
    }

    //矩阵A的p次幂
    public static int[][] powMatrixAitsPCiMi(int[][] A, int p){
        int m = A.length;
        int n = A[0].length;
        //初始化，a=I，t=A的1次方
        int[][] a = new int[m][n];
        for (int i = 0; i < m; i++) {
            a[i][i] = 1;//单位阵
        }
        int[][] tmp = A;//基数矩阵

        //（1）p的0位x=1：a=a×t=1×A的1次方=A的1次方，t=t×t=A的2次方
        //（2）p的1位x=1：a=a×t=A的1次方=A的1次方×A的2次方，t=t×t=A的4次方
        //（3）p的2位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方~~ ，t=t×t=A的8次方
        //（4）p的3位x=1：a=a×t=A的1次方=A的1次方×A的2次方×A的8次方，t=t×t=A的16次方
        //（5）p的4位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方×A的8次方~~ ，t=t×t=A的32次方
        //（6）p的5位x=0：~~a=a×t=A的1次方=A的1次方×A的2次方×A的8次方~~ ，t=t×t=A的64次方
        //（7）p的6位x=1：a=a×t=A的1次方=A的1次方×A的2次方×A的8次方×A的64次方 ，t=t×t=A的128次方
        //此时a已经是A的p=75次方了
        //看p的x位是否为1
        for(; p != 0; p >>= 1){//每次结束p往右移动1位，p=0结束
            if ((p & 1) != 0){
                //p最右那个x位=1，需要雷×结果
                a = matrixMul(a, tmp);//a=a*t
            }
            //每次t都需要倍次幂
            tmp = matrixMul(tmp, tmp);//t=t*t
        }

        return a;//返回a
    }

奶牛问题的手撕代码，关键是矩阵幂次表达式也要熟悉：f(n),f(n-1),…,f(n-k+1)=f(k),f(k-1),…,f(1)×d的n-k次幂。
奶牛问题的d也要记住。

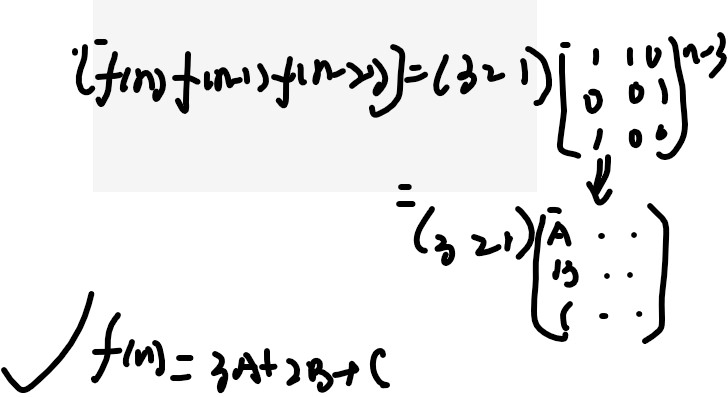
//奶牛生牛问题：
    //d矩阵=1 1 0
    //     0 0 1
    //     1 0 0
    //记住了，
    // f(n)=f(n-1)+f(n-3)
    // 其中，f(1）=1；f(2）=2；f(3）=3；
    //f(n),f(n-1),f(n-2) = 3 2 1 × d的n-3次幂
    public static int fNaiNiuPowAistPCiMi(int n){
        if (n < 1) return 0;
        if (n == 1) return 1;
        if (n == 2) return 2;
        if (n == 3) return 3;

        int[][] d = {
                {1,1,0},
                {0,0,1},
                {1,0,0}
        };//记住d
        int[][] mk = {{3,2,1}};//1行3列的初始化矩阵
        d = powMatrixAitsPCiMi(d, n - 3);//求n-3次幂
        int[][] ans = matrixMul(mk, d);//得到1*3，00就是我们要的f(n)

        //用矩阵乘法的话：00位置
        //return ans[0][0];

        //或者直接用d即可，省掉矩阵乘法
        return 3 * d[0][0] + 2 * d[1][0] + d[2][0];
    }

    public static void test2(){
        System.out.println(fNaiNiuDP2(7));
        System.out.println(fNaiNiuPowAistPCiMi(7));
    }

    public static void main(String[] args) {
//        test();
        test2();
    }

代码中可以省掉矩阵乘法：matrixMul
也可以不省掉，反正省掉节约时间，也都行的。问题不大

结果：很OK哦！

13
13

如果在面试场上，您能想到这个优化方案，绝对不赖！！！

额外一个题：上面的情况再加，奶牛5年就死亡，那第n年又有多少牛？

其实原来能有多少头?
f(n)=f(n-1)+f(n-3)
啥意思呢，上一年的牛，的基础上，咱们新增了多少数量呢？3年前牛的总数，3年前那些牛，都会再生一头，你说是不是加f(n-3)呢？
对吧？？

那么现在，五年就会死一个，那把五年前活着的牛都干死，岂不就是第n年的牛？减f(n-5)完事！

所以答案就是:上面的情况再加，奶牛5年就死亡，那第n年又有多少牛？
f(n)=f(n-1)+f(n-3)-f(n-5)

如何撸代码，按照上面的流程走一遭就行了。

---

总结

提示：重要经验：

1）斐波那契数列作为引导，关键问题在于写暴力递归公式，然后笔试可以改记忆化搜索法，面试可以用精细化动态规划转移方程，面试也能用矩阵幂次法，当然过程中可以省掉矩阵乘法，只写矩阵幂次函数pow；
2）类似斐波那契数列的定义式，f(n)=c1f(n-1)+c2f(n-2)+…+ck*f(n-k)类似的大厂们会经常改编题目来考，另外，矩阵幂次表达式也要熟悉：f(n),f(n-1),…,f(n-k+1)=f(k),f(k-1),…,f(1)×d的n-k次幂。也要熟悉。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。