【排序】快速排序+简单选择排序+堆排序

快速排序

基于“交换”的排序：根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置

算法思想

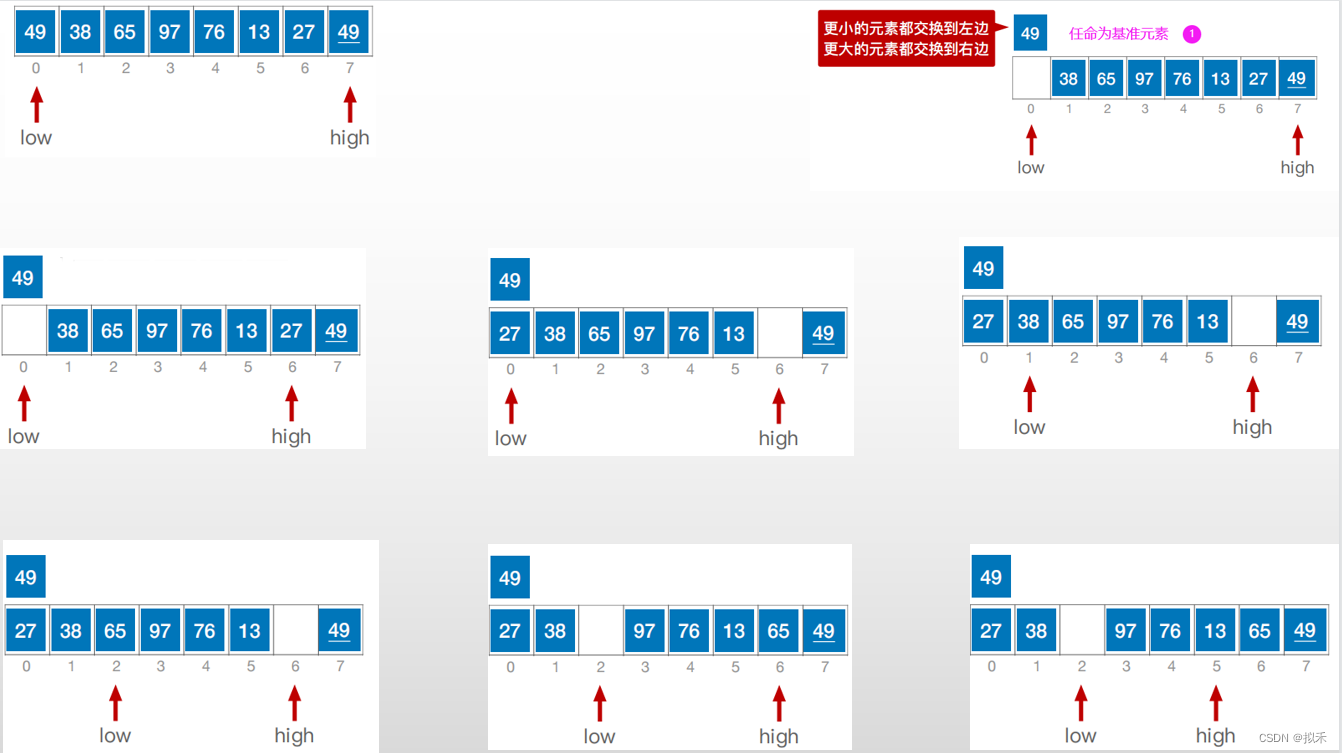
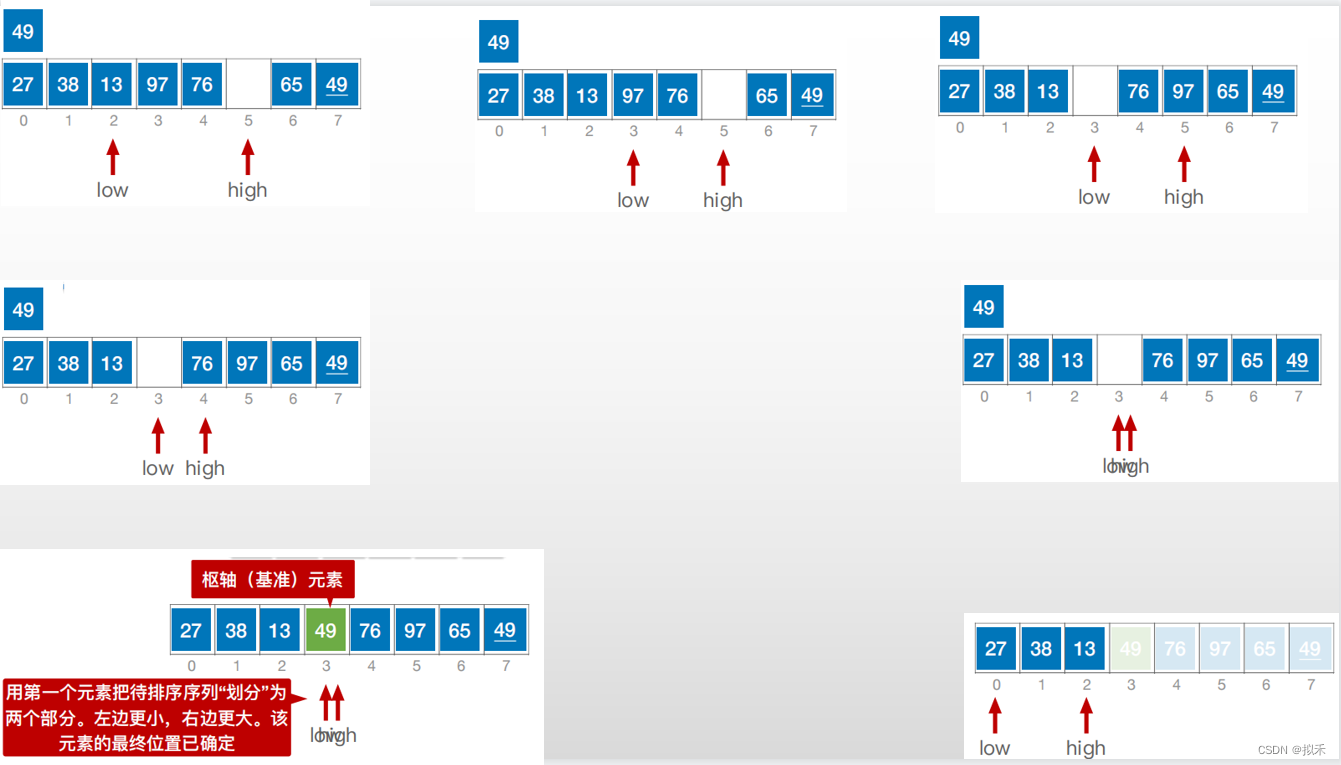
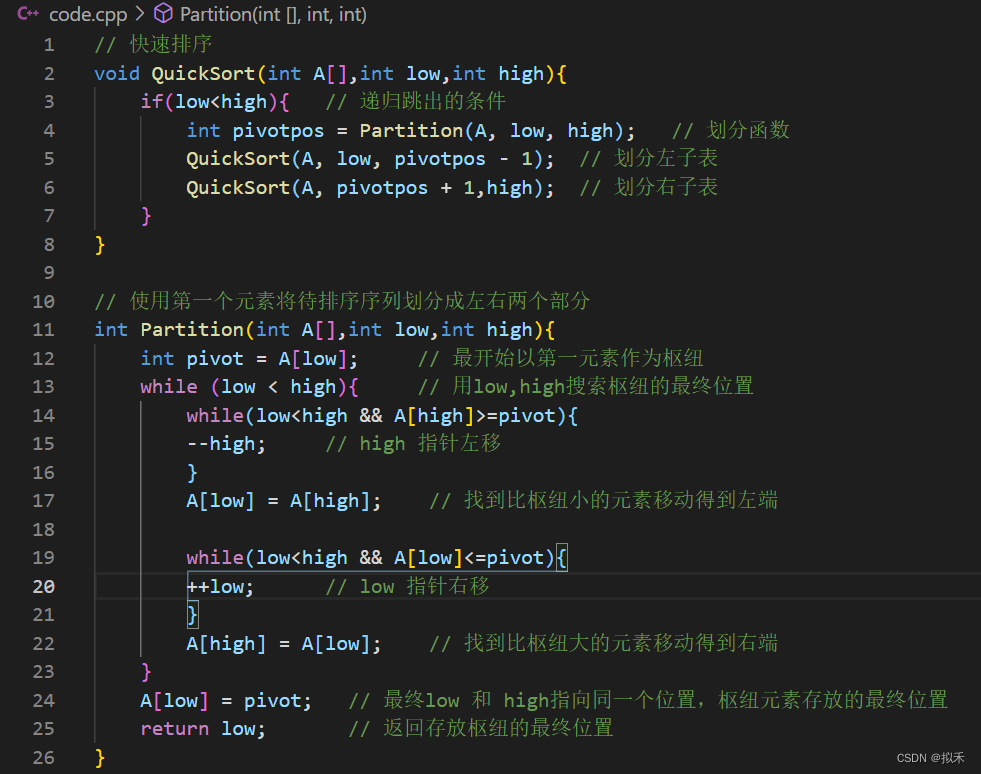
1. 在待排序表L[1..n]中任取一个元素pivot作为枢轴（或基准，通常取首元素)；
2. 通过一趟排序将待排序表划分为独立的两部分L[1..k-1]和LIk+1..n]，使得L[1...k-1]中的所有元素小于pivot，L[k+1..n]中的所有元素大于等于pivot，则pivot放在了其最终位置L(k)上，这个过程称为一次“划分”。
3. 然后分别递归地对左右子表重复上述过程，直至每部分内只有一个元素或空为止，即所有元素放在了其最终位置上。
4. 该算法不稳定

一次划分

---

---

Code

---

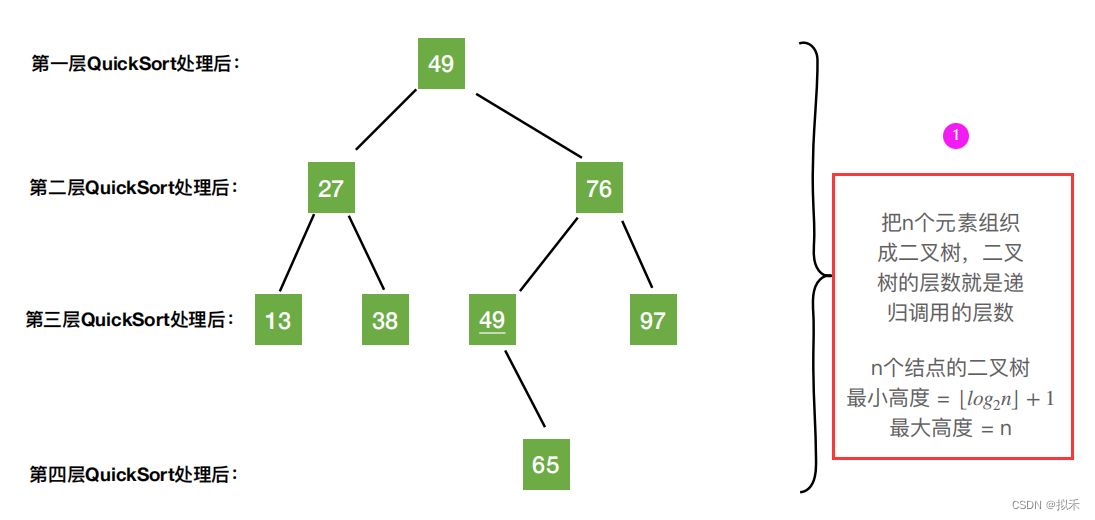
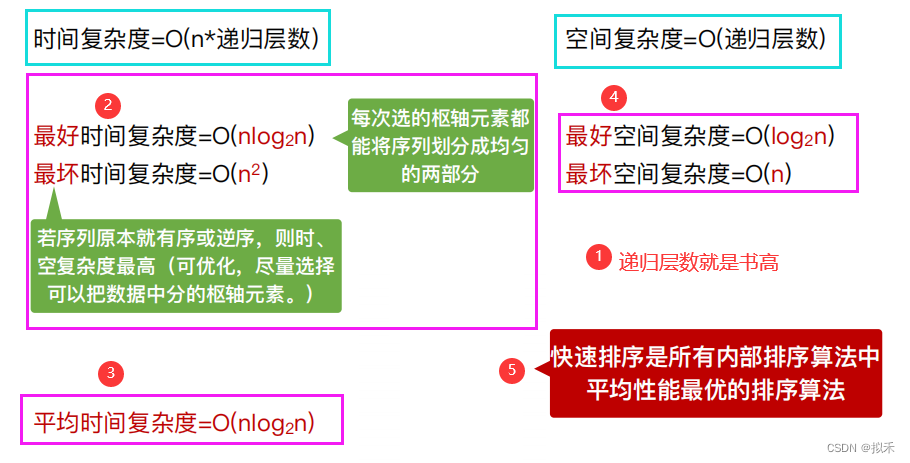
算法效率分析

---

---

---

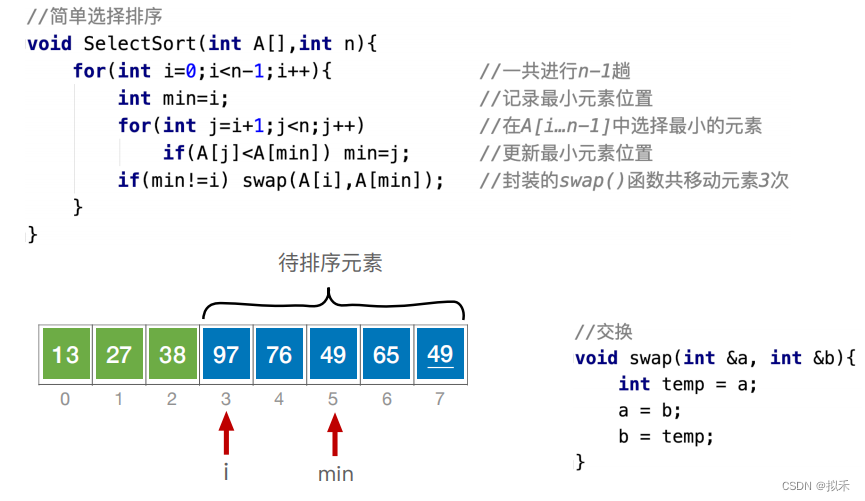
简单选择排序（Easy）

选择排序：每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列

Code

---

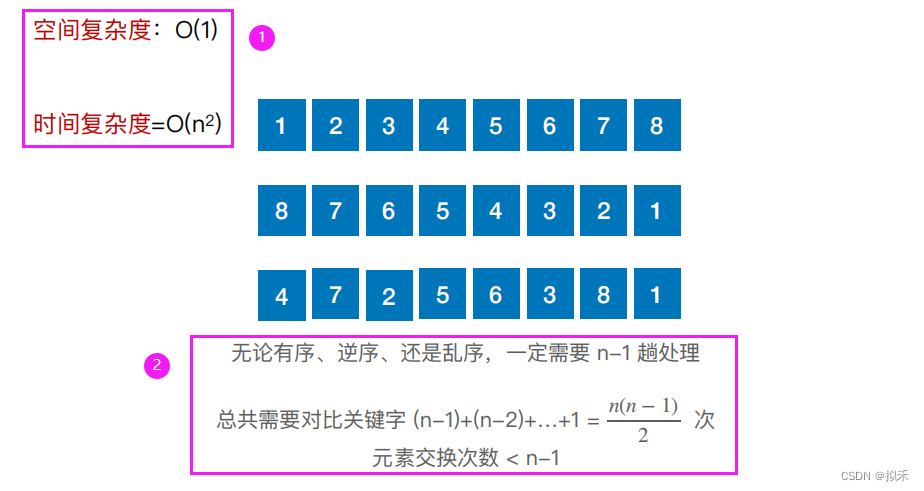
算法性能分析

---

小结

• 该算法不稳定
• 适用性：既可以用于顺序表，也可用于链表
• 必须进行 n-1 趟处理

---

堆排序

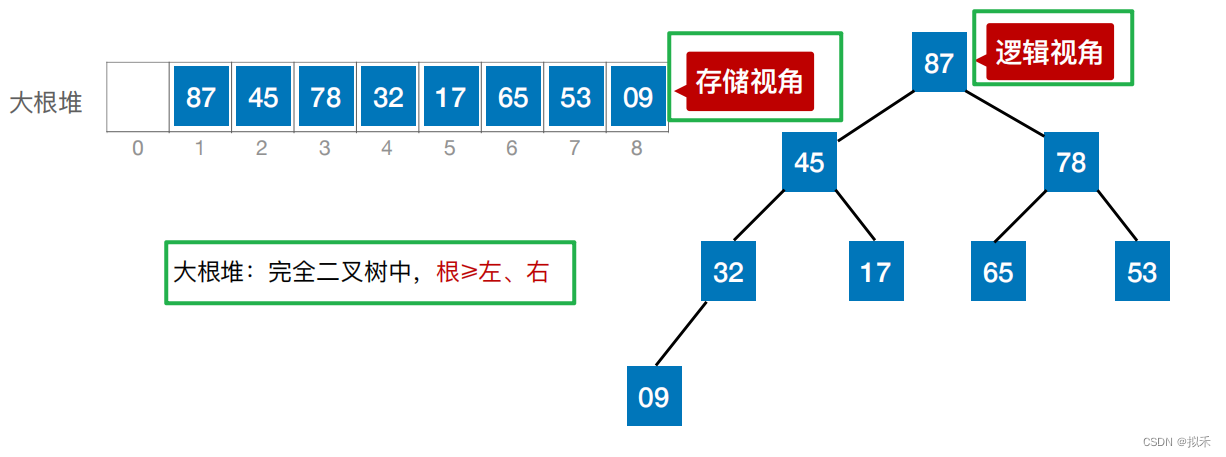
一图胜千言

---

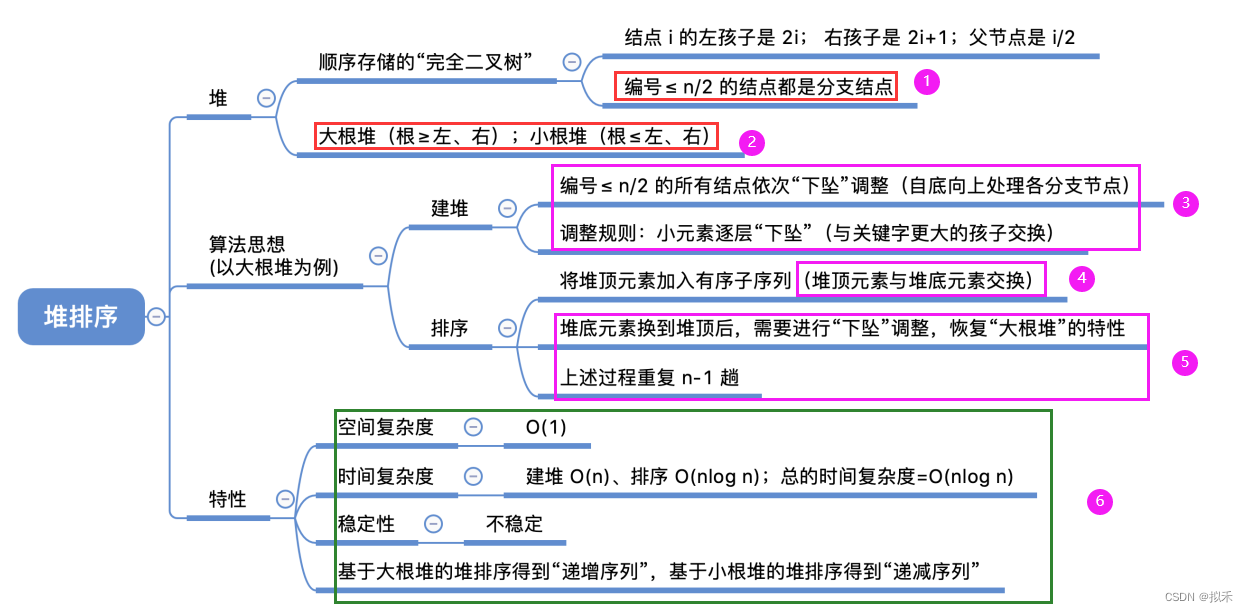
堆（Heap）

---

---

Code

建堆：

• 把所有非终端结点都检查一遍，是否满足大根堆的要求，如果不满足，则进行调整
• 检查当前结点是否满足 根 ≥ 左、右
• 若不满足，将当前结点与更大的一个孩子互换
• 若元素互换破坏了下一级的堆，则采用相同的方法继续往下调整(小元素不断“下坠”)

堆排序：

• 每一趟将堆顶元素加入有序子序列(与待排序序列中的最后一个元素交换)
• 并将待排序元素序列再次调整为大根堆(小元素不断“下坠”)

---

算法效率分析

---

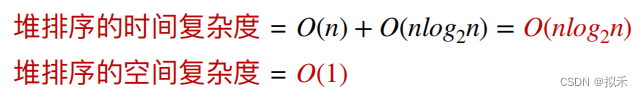
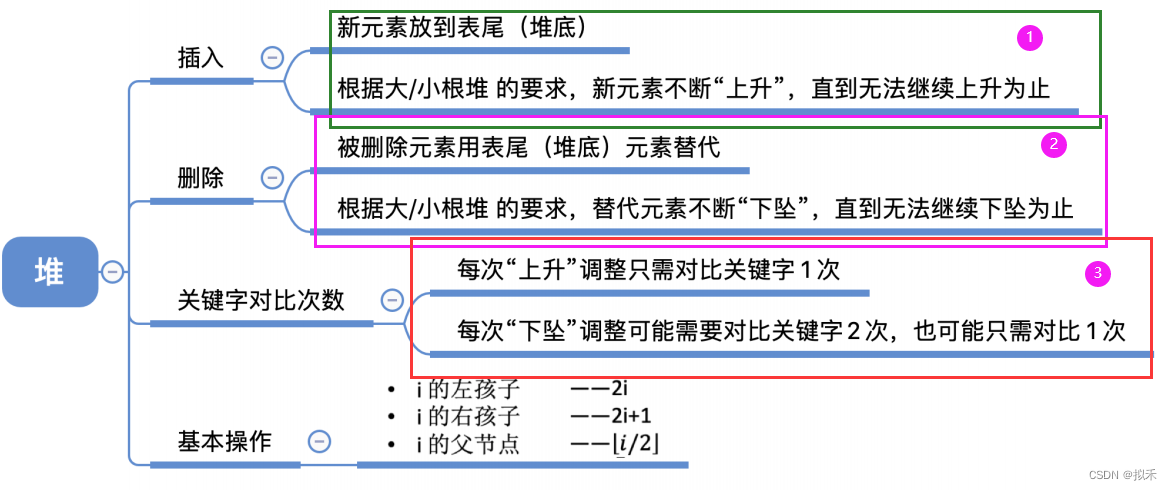
堆的插入与删除

1. 对于小根堆，待插入的新元素放到表尾，与父节点对比，若新元素比父节点更小，则将二者互换。
2. 新元素就这样一路“上升”，直到无法继续上升为止
3. 被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止