验证哥巴赫猜想

题目：算法时间性能的经验分析（验证哥巴赫猜想）
验证哥德巴赫猜想。统计其关键语句的执行次数。并绘制规模-执行次数散点图。
(Goldbach Conjecture)猜想:即任一大于2的偶数都可写成两个质数之和。请验证这个对于较大的偶数都是成立的。
算法:goldbach(n)
描述∶算法验证对于小于等于n的偶数，歌德巴赫猜想都是成立的。注意，goldbach(200)并非验证200可以拆分成两个质数的和，而是验证对于所有≤n的偶数，都可以拆分成两个质数的和。
输入:整数n
输出:1表示成立;0表示猜想有误
注1:用excel绘制散点图，excel可以打开csv格式的文件。
注2∶csv(comma seperated values)是如下格式的文件。
文件位置：

public class Goldbach {

    /**
     * @param args
     * @throws IOException
     */
    public static int cnt;

    public static List list = new ArrayList();

    public static int ARR_SIZE = 2500;

    public static int[] arr = new int[ARR_SIZE];

    public static void main(String[] args) throws IOException {
        Writer file = new FileWriter("diagram.csv");
        file.write("n,times\n");
        String line;
        cnt = 0;
        primes();
        for (int n = 200; n <= 5000; n += 50) {
            int temp = cnt;
            cnt = 0;
            if(n == 200){
                cnt += temp;
            }
            if (passGoldConj(n)) {
                line = Integer.toString(n) + "," + Integer.toString(cnt) + "\n";
                file.write(line);
            } else {
                System.out.println("Goldbach conjuction doesn't hold in our test");
                break;
            }
        }
        file.close();
    }

    public static boolean isPrime(int n) {
        if (list.indexOf(n) != -1){
            return true;
        }
        return false;
    }

    public static boolean passGoldConj(int n) {
        int k = 0;
        for (int i = 4; i <= n; i += 2 ){
            cnt++;
            for(int j = 2; j < i; j++) {
                cnt++;
                if (isPrime(j) && isPrime(i - j)) {
                    k++;
                    break;
                }
            }
        }
        if (k == (n/2 - 1)) {
            return true;
        }
        return false;
    }


	//这里使用的是筛选法求质数因子
    public static void primes(){
        arr[0] = 2;
        for (int i = 1, j = 3; i < ARR_SIZE; i++,j += 2){
            cnt++;
            arr[i] = j;
        }
        for (int i = 1; i < ARR_SIZE; i++) {
            cnt++;
            if (Math.pow(arr[i], 2) <= ARR_SIZE*2 && arr[i] != 0){
                int j, temp;
                temp = arr[i];
                //相比日常的筛选法，改进了一下
                for (j = temp * temp; j <= ARR_SIZE*2; j += 2*temp) {
                    cnt++;
                    int index = (j-1)/2;
                    arr[index] = 0;
                }
            }
        }

        for (int i = 0; i < ARR_SIZE; i++) {
            cnt++;
            if (arr[i] != 0) {
                list.add(arr[i]);
            }
        }
//        System.out.println(list);
//        System.out.println(list.size());
    }
}

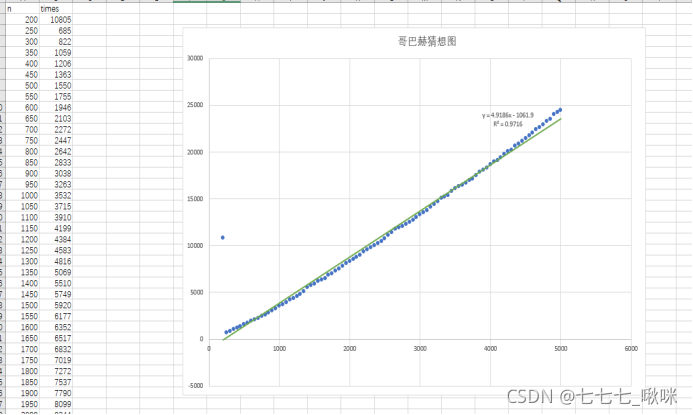
时间复杂度是近乎O(n)，线性的，但是求第一个质数是很废时间的，因为我是将某数以内的所需质数全部求出。

纯属记录分享，会有更好的方法