动态规划求解最长公共子序列_采用动态规划算法求解下列两个数组的最长公共子序列:a={a,c,g,m,o,o,d}和b={a-优快云博客

本文详细阐述了如何使用动态规划策略解决最长公共子序列问题，通过一维和二维数组存储数据，提供了三个测试用例，并展示了C++代码实现。算法复杂度控制在O(m*n)，涉及递归、路径记录和子序列构建。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.实验要求
采用动态规划策略设计并实现算法，求解最长公共子序列问题。要求算法的复杂度不超过O(m*n)。

2.算法基本思想
运用递归将求出两个序列中元素相同的路径，然后找出其最长公共子序列。

3.主要数据结构及其作用
一维数组、二维数组：存储纪录数据和位置.

4.测试用例

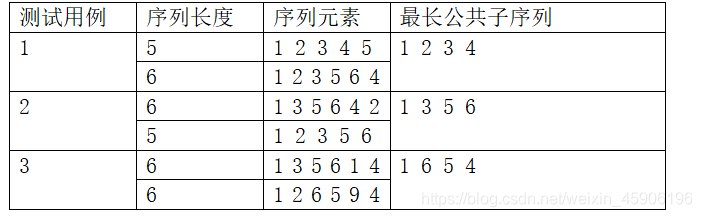
5.运行结果截图

测试用例1

测试用例2

测试用例3
6.代码实现

#include<iostream>
using namespace std;
void LCSLength(int m,int n,char *x,char *y,int **c,int **b){
	int i,j;
	for(i=1;i<=m;i++)
		c[i][0]=0;
	for(i=1;i<=n;i++)
		c[0][i]=0;
	for(i=1;i<=m;i++){
		for(j=1;j<=n;j++){
			if(x[i]==y[j]){
				c[i][j]=c[i-1][j-1]+1;
				b[i][j]=1;
			}
			else if (c[i-1][j]>=c[i][j-1]){
				c[i][j]=c[i-1][j];
				b[i][j]=2;
			}
			else{
				c[i][j]=c[i][j-1];
				b[i][j]=3;
			}
		}
	}
}
void LCS(int i,int j,char x[],int **b){
	if(i==0||j==0)
		return ;
	if(b[i][j]==1){
		LCS(i-1,j-1,x,b);
		cout<<x[i]<<" ";
    }
    else if(b[i][j]==2)
    	LCS(i-1,j,x,b);
    else
    	LCS(i,j-1,x,b);
}
int main()
{
    int m,n;
    char x[100],y[100];
    int **b,**c;
    cout<<"请分别输入两个序列的长度："<<endl;
    cin>>m>>n;
    cout<<"请输入第一个序列："<<endl;
    for(int i=0;i<m;i++){
		cin>>x[i];
        cout<<x[i];
	}
        cout<<endl;
    cout<<"请输入第二个序列："<<endl;
    for(int i=0;i<n;i++){
		cin>>y[i];
        cout<<y[i];
	}
	cout<<endl;
    LCSLength(m,n,x,y,c,b);
    LCS(m,n,x,b);
    cout<<endl;
}