/*可逆素数是指一个素数的各位数字顺序地倒过来构成的数仍然是素数*/
#include<stdio.h>
#include<math.h>
main()
{
int ss(int);
int num,num2,a,b,c,d,m,n,count=0;
for(num=1000;num<10000;num++)
{
m=judge(num);
a=num/1000;//原来数的千位
b=num%1000/100;//原数百位
c=num%100/10;//原数的十位
d=num%10;//原数的个位
num2=d*1000+c*100+b*10+a;//倒序组成的数字
n=judge(num2)
if(m==1&&n==1&&num<num2)//1009和9001为可逆的,所以通过num<num2输出1个就可以
{
printf(" %d ",num);
count++;
if(count%10==0)
printf("\n");
}
}
printf("\n");
}
int judge(int a)//判断数字是不是素数
{
int i;
if(a==1)
return 0;
if(a==2)
return 1;
for(i=2;i<=sqrt(a);i++)
if(a%i==0)
break;
if(i>sqrt(a))
return 1;
else
return 0;
}运行的结果: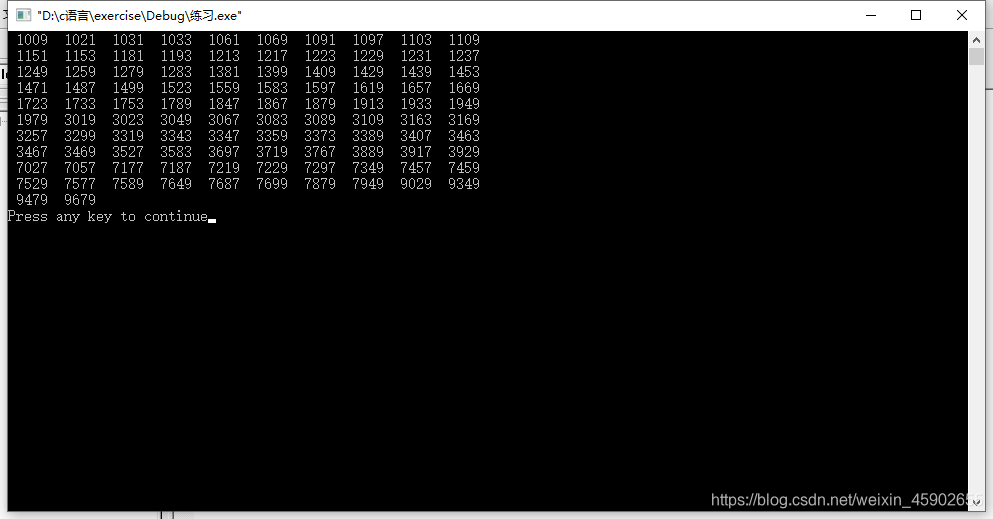
























 3346
3346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








