常见数据结构

1.顺序表-链表

顺序表和链表是数据结构中的两种存储形式。
顺序表(值得是典型的数组)，它的原理：将数据放到一块物理地址连续的存储空间中。顺序表的优点：1.空间利用率高。2.读取速度快可以根据下标去读取。顺序表的缺点：1.插入和删除比较慢。删除和插入元素后此元素后面的元素都要动。2.不可以增加长度，有空间限制。适用场景：适用于表长度变化不大场景。多查找，少插入删除。

链表原理：在程序运行过程中动态分配空间，只要存储器有空间，就不会发生存储溢出问题，相邻元素不要求在物理地址上相邻，在逻辑上相邻即可。所存储的空间分为两部分，一部分用来存储节点值，另一部分用来存储节点间关系的指针。链表的优点：1.插入和删除的速度快，保留原来的物理地址。2.没有空间限制，只与内存空间的大小有关。3.动态分配内存空间，不用事先开辟内存。链表的缺点：1.需要占取额外的空间去存储指针，浪费空间。2.查找速度慢，每次都需要从开始节点开始查找。适用场景：适用于频繁的插入删除操作。适用于线性长度变化大。

#ArrayList, LinkedList, Vector 的区别是什么?
ArrayList: 内部采用数组存储元素，支持高效随机访问，支持动态调整大小
LinkedList: 内部采用链表来存储元素，支持快速插入/删除元素，但不支 持高效地随机访问
Vector: 可以看作线程安全版的 ArrayList,使用了synchronized来实现线程同步，所以ArrayList性能方面由于Vector。ArryList和Vector都会根据实际的动态调整容量，只不过在Vector扩容每次增加1倍，而ArrayList每次增加50%.

2.哈希

Hash：是一种信息摘要算法，它还叫做哈希，或者散列。我们平时使用的MD5,SHA1都属于Hash算法，通过输入key进行Hash计算，就可以获取key的HashCode()，比如我们通过校验MD5来验证文件的完整性。

哈希表：也叫做散列表。是根据关键码值（key value）进行访问的数据结构。查找效率即时间复杂度为O(1)。即通过关键码值映射到表中的一个位置来访问，以加快查找的速度，这个映射函数叫做哈希函数，存放记录的数组叫做哈希表。

碰撞：不同的关键字同通过哈希函数计算出相同的哈希地址，这种现象称为哈希冲突或哈希碰撞。就算是MD5这样优秀的算法也会发生碰撞，即两个不同的key也有可能生成相同的MD5。

解决哈希碰撞：①闭散列，也叫开放定址法：当发现哈希冲突，如果哈希表未被填满，说明哈希表中必然有空位置，那么可以把key存放到冲突位置中的“下一个”空位置去。寻找空位置有：线性探测和二次探测两种。二次探测可以防止聚集的产生；但是二次探测法也会导致二次聚集的产生。
线性探测中，如果哈希函数计算的原始下标是x, 线性探测就是x+1, x+2, x+3, 以此类推；而在二次探测中，探测的过程是x+1, x+4, x+9, x+16，以此类推，到原始位置的距离是步数的平方。

②开散列，也叫链地址法。链地址法的实现原理就是使用数组加链表，在哈希表每个单元中设置链表，当出现冲突后，不需要在原始的数组中寻找空位，而是将其他同样映射到这个位置的数据项加到链表中。

#如果HashMap的大小超过了负载因子(load factor)定义的容量，怎么办？

默认的负载因子大小为0.75，当一个map填满了75%的bucket时候，和其它集合类(如ArrayList等)一样，将会创建原来HashMap大小的两倍的bucket数组，来重新调整map的大小，并将原来的对象放入新的bucket数组中。这个过程为rehashing，因为它调用hash方法找到新的bucket位置

3.栈和队列

栈和队列，也属于线性表，因为它们也都用于存储逻辑关系为 "一对一" 的数据。栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构，同顺序表和链表一样，也是用来存储逻辑关系为 "一对一" 数据。队列是一种要求数据只能从一端进，从另一端出且遵循 "先进先出" 原则的线性存储结构。

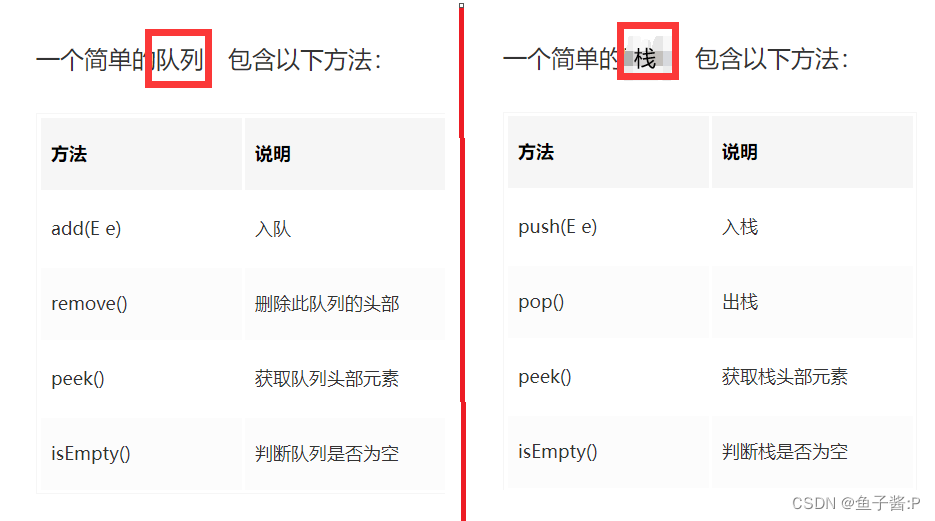
区别：（1）操作的限定不同。队列是在队尾入队，队头出队，即两边都可操作。而栈的进栈和出栈都是在栈顶进行的，无法对栈底直接进行操作。（2）操作的规则不同。队列是先进先出，而栈为后进先出（3）遍历数据速度不同。队列是基于地址指针进行遍历，而且可以从头部或者尾部进行遍历，但不能同时遍历，无需开辟空间，因为在遍历的过程中不影响数据结构，所以遍历速度要快。栈是只能从顶部取数据，也就是说最先进入栈底的，需要遍历整个栈才能取出来，而且在遍历数据的同时需要为数据开辟临时空间，保持数据在遍历前的一致性
 

#用栈实现队列

思路：两个栈，一个进，一个出，pop()和peek()的功能类似，抽象出来以复用。

class MyQueue {
    Stack<Integer> stackIn;
    Stack<Integer> stackOut;
    public MyQueue() {
        stackIn = new Stack<>();
        stackOut = new Stack<>();
    }
    
    public void push(int x) {
        stackIn.push(x);
    }
    
    public int pop() {
        dumpstackIn();
        return stackOut.pop();
    }
    public void dumpstackIn(){
        if(!stackOut.isEmpty()){
            return;
        }
        while(!stackIn.isEmpty()){
            stackOut.push(stackIn.pop());
        }
    }
    
    public int peek() {
        dumpstackIn();
        return stackOut.peek();
    }
    
    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }
}

#用队列实现栈

思路：依旧用两个队列，只不过没有输入和输出的关系，而是另一个队列完全用又来备份的

 

class MyStack {
    Queue<Integer> que1;
    Queue<Integer> que2;
    public MyStack() {
        que1 = new LinkedList<>();
        que2 = new LinkedList<>();
    }
    
    public void push(int x) {
        que2.offer(x);
        while(!que1.isEmpty()){
            que2.offer(que1.poll());
        }
        Queue<Integer> tmp;
        tmp = que1;
        que1 = que2;
        que2 = tmp;
    }
    
    public int pop() {
        return que1.poll();
    }
    
    public int top() {
        return que1.peek();
    }
    
    public boolean empty() {
        return que1.isEmpty();
    }
}

 

4.二叉树

定义：二叉树是每个节点最多有两个子树的树结构，即二叉树中不存在度大于二的节点。并且，二叉树的子树有左右之分，其次序不能颠倒。

树： 树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合 

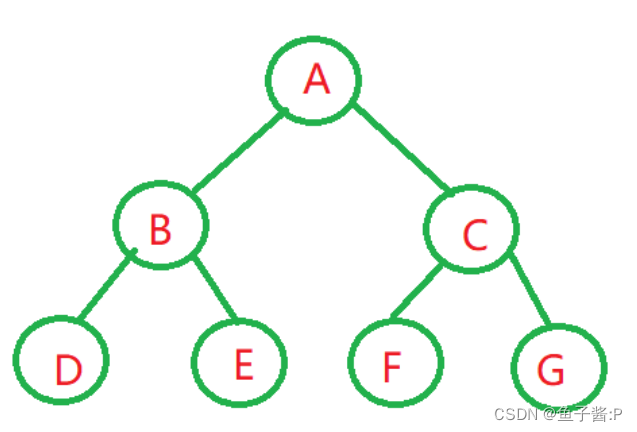
1. 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为2。
2. 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为2。
叶子节点或终端节点：度为0的节点称为叶节点； 如上图：D E F G节点为叶节点。
3. 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点，B是D和E的节点。
4. 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点，F和G是C的孩子结点。
5. 根结点：一颗树中没有双亲结点的结点就叫为根结点，如图：A。
6.节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
7. 树的高度或深度：树中节点的最大层次； 如上图：树的高度为3。

二叉树的特点：

1. 每个结点最多有两棵子树，即二叉树不存在度大于 2 的结点。
2. 二叉树的子树有左右之分，其子树的次序不能颠倒，因此二叉树是有序树。

两种特殊的二叉树
1. 满二叉树: 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
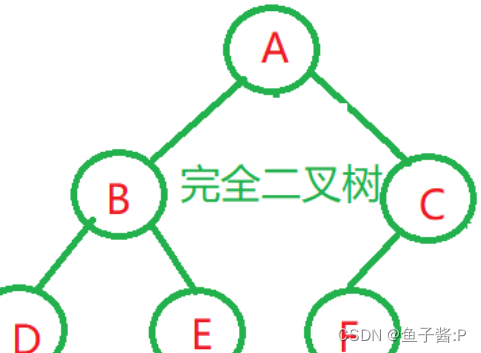
2. 完全二叉树: 除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。满二叉树是一种特殊的完全二叉树。堆就是一棵完全二叉树。

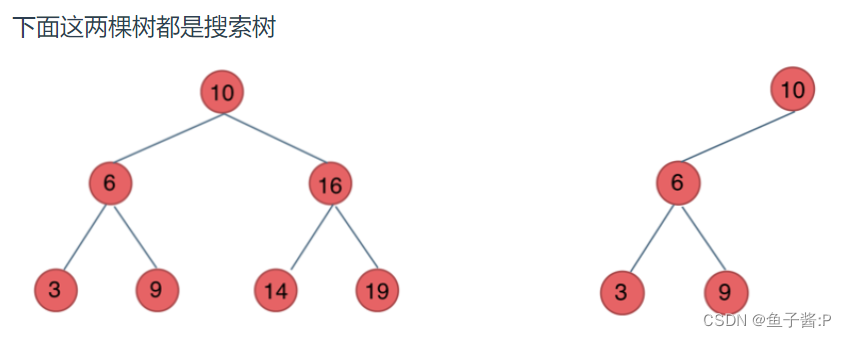
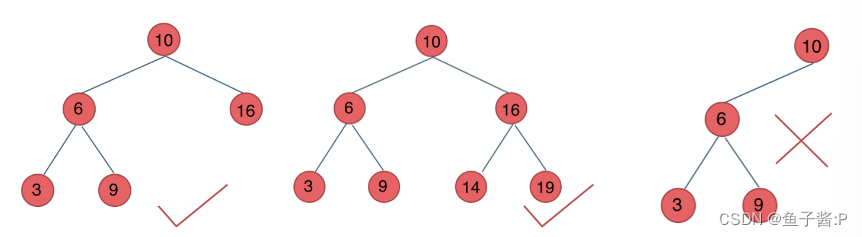
二叉搜索树是一个有序树。 

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

 平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 二叉树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

// 孩子表示法
class TreeNode {
 int val; // 数据域
 TreeNode left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
 TreeNode right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class TreeNode {
 int val; // 数据域
 TreeNode left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
 TreeNode right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
 TreeNode parent; // 当前节点的根节点
}
一般来说，孩子表示法用的更多

二叉树定义：

public class TreeNode {
    int val;
  	TreeNode left;
  	TreeNode right;
  	TreeNode() {}
  	TreeNode(int val) { this.val = val; }
  	TreeNode(int val, TreeNode left, TreeNode right) {
    		this.val = val;
    		this.left = left;
    		this.right = right;
  	}
}

 二叉树得掌握的基础代码

①二叉树两种遍历方式：

1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
2. 广度优先遍历：一层一层的去遍历。

②二叉树最大深度，最小深度（完全二叉树的结点个数与这道题很像！）

③翻转二叉树：新建函数

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        invertTree(root.left);
        invertTree(root.right);
        swap(root);
        return root;
    }
    public void swap(TreeNode root){
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

④对称二叉树（镜像二叉树）：新建函数

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left,root.right);
    }
    private boolean compare(TreeNode u,TreeNode v){
        if(u==null && v==null){
            return true;
        }
        if(u==null || v==null || u.val!=v.val){
            return false;
        }
        return compare(u.left,v.right) && compare(u.right,v.left);
    }
}