（中石油六）问题 K: 水果传送（去暴力+找规律）

问题 K: 水果传送

题目描述
联欢会开始了，同学们按对应的组别已整齐安静的就坐。此时小Z发现为同学们准备的水果还没有派发。各小组已紧密的连成了一排，于是他想了个办法，从两端将水果一个一个传送给各组，直到满足各组水果要求个数为止。假设每秒他只能在两端各传送一个水果，求T秒后各组中的水果数。
传送办法是：各组拿到水果后都向中间方向的相邻组传送（最中间的不用传），直到相邻组满足要求为止。举例：小组数M＝5，各组要求水果数K=4。
第1秒

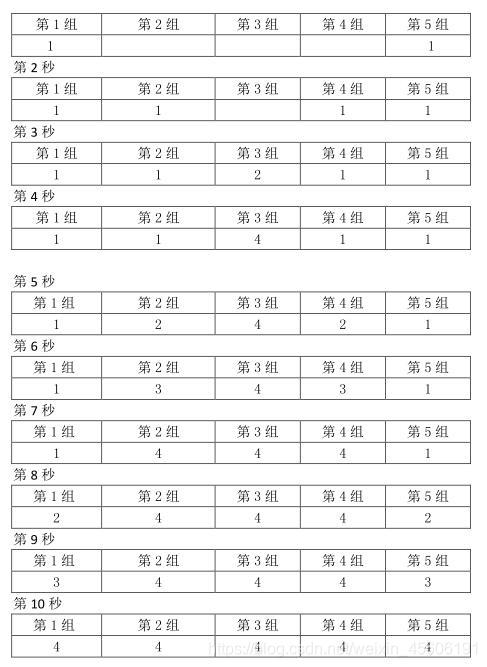
输入
输入三个正整数，分别是组数M，每组需要的水果数K，时间T，它们的范围[1…100000]。
数据保证M为奇数，K为偶数。T<=M*K/2。
输出
输出传送T秒后，各组别的水果数。
样例输入 Copy
5 4 5
样例输出 Copy
1 2 4 2 1

先附上我原本错误的答案，尾递归超时，无脑流，一次一次加。
这里顺便提一下#pragma GCC optimize(2)这个读入挂，虽然可以在遇到大数据时帮您照样输出，但超时依旧，只是帮你检查一下结果的作用。个人感觉没什么大用。

//尾递归超时
#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
typedef long long ll;
int m,k,t,a[50002],mid;
void dfs(int n){
	if(n==t){
		for(int i=1;i<=mid;i++){
			if(i==1)	printf("%d",a[i]);
			else	printf(" %d",a[i]);
		}
		for(int i=mid-1;i>0;i--){
			printf(" %d",a[i]);
		}
		return;
	}
	else if(n==0){
		a[1]++;
	}
	else{
		a[1]++;
		for(int i=mid-1;i>0;i--){
			if(a[i]==0)	continue;
			else if(a[i+1]<k){
				a[i]--;
				if(i+1==mid)	a[mid]+=2;
				else	a[i+1]++;
			}
		}
	}
	dfs(n+1);
}
int main(){
	scanf("%d%d%d",&m,&k,&t);
	mid=(m+1)/2;
	dfs(0);
}

很明显复杂度O(n)=O(x^n)，当然尾递归（自上而下）也可以改善，降成O(n)，比如备忘录、二分查找、正序（自下而上）等等，但本质和找规律差不多（其实是有点区别的），下面给一种类二分的。
其实这题可以发现左右对称，只有中间特殊，一遍的规律也很容易找出，所以就分类吧。
将它分成3种情况。
1、还没到加到中间。
2、到中间了但是中间数没有超过k值。
3、到中间了且超过k。
PS：这代码还是小编自己抄别人的，自己实在太懒了。

#include <bits/stdc++.h>
using namespace std;
int a[100001];
int main(){
    int mid,m,k,t,b,c;
    scanf("%d%d%d",&m,&k,&t);
    mid=m/2+1;		//中间数
    c=t-m/2;		//剩下的时间
    b=k/2;			//半对半时间
    
    if(t<mid){			//还没到mid 
        for(int i=1; i<=t; i++)		a[i]=1;
    }
	else if(t>=mid){
        for(int i=1; i<mid; i++)	a[i]=1;	//初始化 
        if(c*2<=k)		a[mid]=c*2;		//mid还未至K 
        else if(c*2>k){			//mid已至K 
            t=c-k/2;
            a[mid]=k;
            for(int i=mid-1;i>0;i--){
            	if(t==0)	break;
                while(a[i]<k&&t){
                    a[i]++;	t--;
                }
            }
        }
    }
    //输出 
    for(int i=1;i<=mid;i++){
		if(i==1)	printf("%d",a[i]);
		else	printf(" %d",a[i]);
	}
	for(int i=mid-1;i>0;i--)	printf(" %d",a[i]);
    return 0;
}