LeetCode--236 二叉树的最近公共祖先

思路一

题目

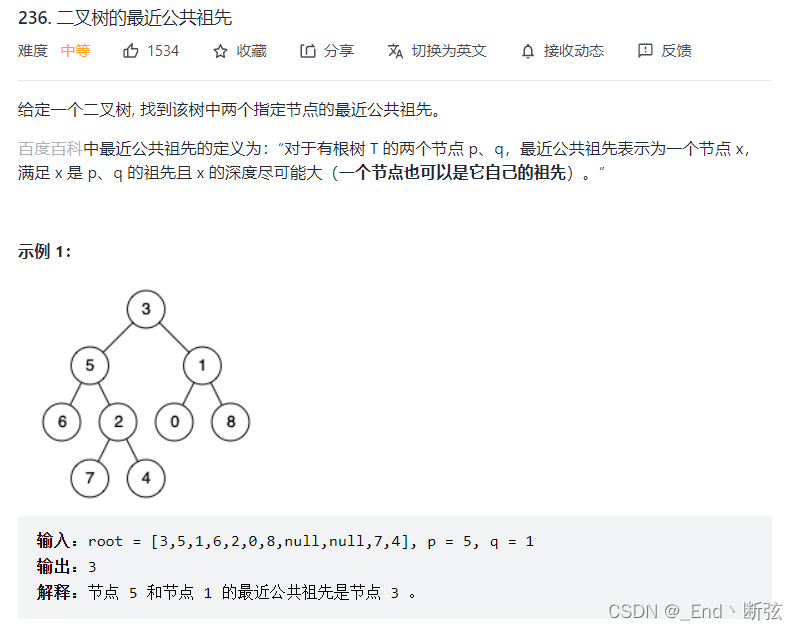
如果面试官问二叉树的最近公共祖先，我们可以问面试官，这个二叉树是不是搜索树，如果是搜索树
如下图：

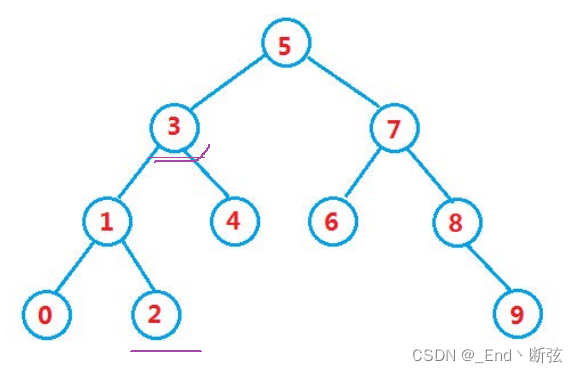
搜索树的特征是：左孩子比父亲小，右孩子比父亲大。那我们可以分析：2,3的最近公共祖先是3，0，4的最近公共祖先是3, 6和9的最近祖先是7。那么可以得出：一个子结点比根小，一个子结点比根大，这个根就是最近公共祖先，如果2个结点中有1个是根节点那么这个结点就是最近公共祖先

普通二叉树

由上面的思路得出：
1.2个结点都在左子树中，递归到左树中找
2.2个结点都在右子树中，递归到右树中找
3.如果1个在左一个在右，根结点就是最近的公共祖先,如果2个结点中有1个是根节点那么这个结点就是最近公共祖先
此时需要写个递归来查找结点，这里要用结点来比较，不能用val来比较，如果val一样就会存在误判的情况。还要注意命名，命名不好容易给别人带来困惑，或者面试官不给分。

代码如下：

class Solution {
public:
 bool find(TreeNode* root,TreeNode* x)
 {
     //root为空直接返回
    if(root == nullptr)
    return false;
    if(root == x)
    return true;
   //不在左子树就到右子树中找，这里用或即可
    return find(root->left,x) || find(root->right,x);

 }
 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
 //如果2个其中有1个是根直接此时根就是最近的公共祖先
        if(p == root || q == root)
        {
            return root;
        }
        //定义4个bool值，分别是p在左子树和右子树
        //q和p一样的即可
        bool pInLeft,pInRght,qInLeft,qInRght;
        //p在左就不会在右子树中
        //q也是相同的操作
        pInLeft = find(root->left,p);
        pInRght = !pInLeft;
        qInLeft = find(root->left,q);
        qInRght = !qInLeft;
       //如果2个都在左子树中，继续递归到左子树找
        if(pInLeft && qInLeft)
        {
            return lowestCommonAncestor(root->left,p,q);
        }
         //如果2个都在右子树中，继续递归到右子树找
        else if(pInRght && qInRght)
        {
            return lowestCommonAncestor(root->right,p,q);
        }
        //一个在左一个在右，根就是最近的公共祖先
        else
        {
            return root;
        }
    }
};

分析：如果二叉树是满二叉树或者完全二叉树，此时的时间复杂度是O(nlogn),极端情况是一条单支的树，此时的时间复杂度是O(N^2)。此时面试官要求时间复杂度是O(N)，那该如何解决呢？

思路二

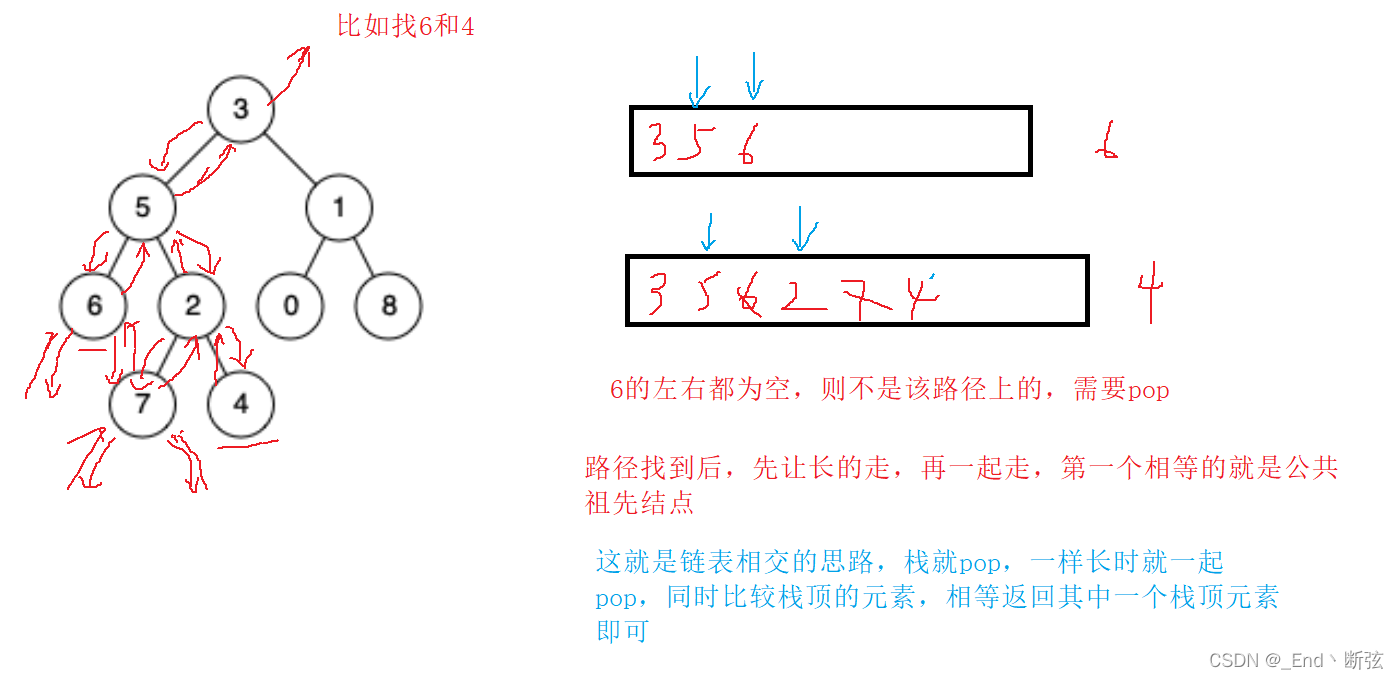
找2个结点的路径，利用栈把路径保存下来，转化为了找相交的结点。

代码如下：

class Solution {
public:
   bool findPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
   {
       if(root == nullptr)
       return false;
       //根节点不为空就进栈
       path.push(root);

       if(root == x)
       return true;
       //找到返回true
       if (findPath(root->left,x,path))
       {
           return true;
       }
        if(findPath(root->right,x,path))
       {
           return true;
       }
       //走到这里就不是该路径的，pop将false返回给上一层
       path.pop();
       return false;
   }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //定义2个栈保存路径
      stack<TreeNode*> pPath;
      stack<TreeNode*> qPath;
      //找到p和q的路径
      findPath(root,p,pPath);
      findPath(root,q,qPath);
      //用2个指针来比较长短
      stack<TreeNode*>*shortPath = &pPath;
      stack<TreeNode*>*longtPath = &qPath;
      //不知道哪个路径长，此时默认其中1个长，在比较，如果默认长的短在交换
      if(pPath.size() > qPath.size())
      {
          swap(shortPath,longtPath);
      }
      //先让长的走差距，在同时走
      while(shortPath->size() < longtPath->size())
      {
         longtPath->pop();
      }
      //同时走且比较栈顶的元素是否相等，第1个相等的即使最近公共祖先
      while(shortPath->top() != longtPath->top())
      {
          longtPath->pop();
          shortPath->pop();
      }
      return shortPath->top();
        }
};

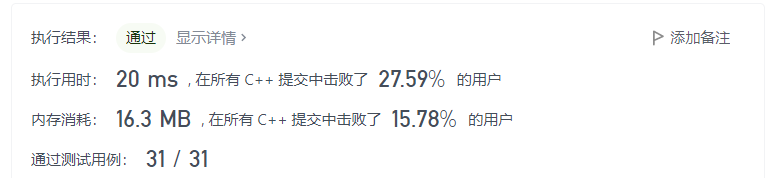
我们就过了。
分析：

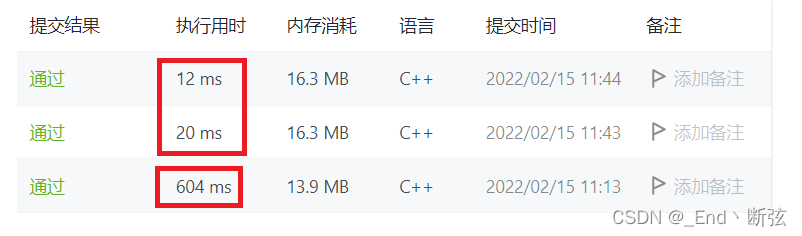
可以看出思路二比一快了很多，时间复杂度分析：2个路径入栈是O(N),2个栈再比较也是O(N),也就是O(4N),最终时间复杂度是O(N)。