机器学习实战--SVM

1、支持向量机概述

SVM是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化。
训练数据线性可分时，通过硬间隔最大化，学习一个线性分器，即线性可分支持向量机，又称为硬间隔支持向量机；训练数据近似线性可分时，通过软间隔最大化，也学习一个线性分类器，即线性支持向量机，也称为软间隔支持向量机；训练数据线性不可分时，通过使用核技巧和软间隔最大化，学习非线性支持向量机。
现在，我们依然对于一个二维平面的简单例子进行推导讲述。
下图将数据集分隔开来的直线称为分隔超平面；由于数据点都在二维平面上，所以此时分隔超平面就只是一条直线。
支持向量就是离分隔超平面最近的那些点。要试着最大化支持向量到分隔面的距离，需要找到此问题的优化求解方法。

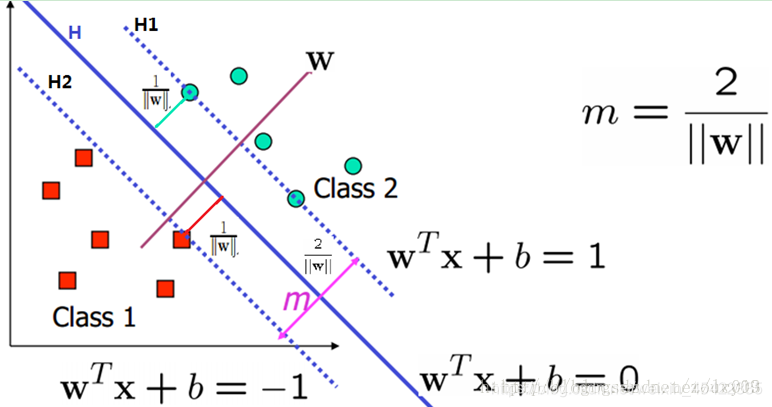
如何求解数据集的最佳分隔直线？寻找最大间隔？
分隔超平面的形式可以写成W（T）X+b =0要计算点支持向量到分隔超平面的距离，就必须给出点到分隔面的法线或垂线的长度。

在约束条件下引入拉格朗日系数，求最值，确定KKT条件，将w和b转化为a来表示；

2、SMO算法

SMO算法的工作原理是：每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha，那么就增大其中一个同时减小另一个。这里所谓的”合适”就是指两个alpha必须符合以下两个条件，条件之一就是两个alpha必须要在间隔边界之外，而且第二个条件则是这两个alpha还没有进进行过区间化处理或者不在边界上。
现在，让我们梳理下SMO算法的步骤：

• 步骤1：计算误差：
  -

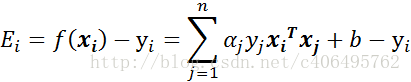
• 步骤2：计算上下界L和H：

• 
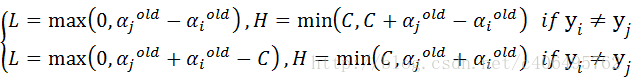
  步骤3：计算η：
  

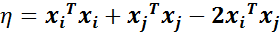
• 步骤4：更新αj：

• 
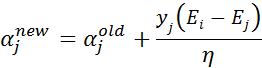
  步骤5：根据取值范围修剪αj：
  

• 步骤6：更新αi：

• 
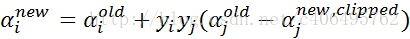
  步骤7：更新b1和b2
  

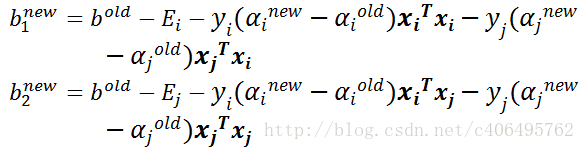
• 步骤8：根据b1和b2更新b：

• 

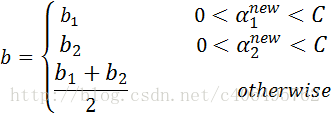
SMO算法代码实现：

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    #转换为numpy的mat存储
    dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
    #初始化b参数，统计dataMatrix的维度
    b = 0; m,n = np.shape(dataMatrix)
    #初始化alpha参数，设为0
    alphas = np.mat(np.zeros((m,1)))
    #初始化迭代次数
    iter_num = 0
    #最多迭代matIter次
    while (iter_num < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            #步骤1：计算误差Ei
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            #优化alpha，更设定一定的容错率。
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                #随机选择另一个与alpha_i成对优化的alpha_j
                j = selectJrand(i,m)
                #步骤1：计算误差Ej
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                #保存更新前的aplpha值，使用深拷贝
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                #步骤2：计算上下界L和H
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                #步骤3：计算eta
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print(