剑指offer- 61~68（完结篇）

61.扑克牌中的顺子（√）

这个题并不简单，有点意思啊！

思路：排序+ 跳过0+判断相邻的是否相差1

public boolean isStraight(int[] nums) {
        Arrays.sort(nums);
        for(int i = 0; i < nums.length;i++){
            if(nums[i] == 0) continue;
            //第二个不是0 但是减去前一个 >1  或者是第二个不是0 但是和前一个相等
            if(i > 0 && nums[i] - nums[i-1] != 1){
                return false;
            }
        }
        return true;
    }

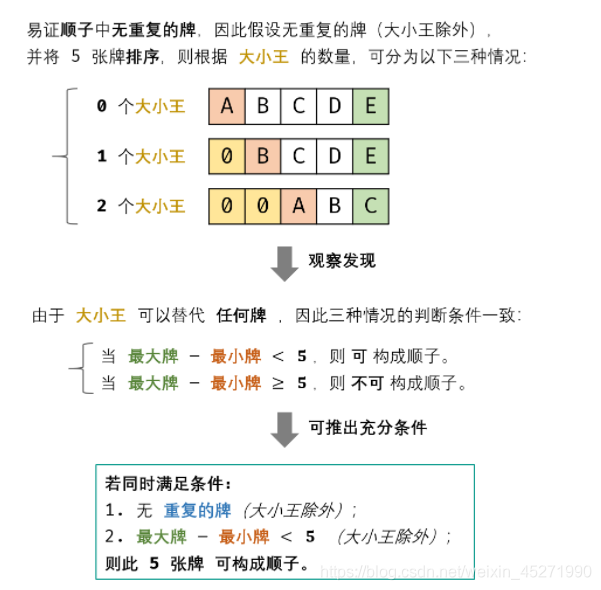
结果出现了一些问题，主要是因为大王小王其实是可以代替任何一张牌的，所以思路上不可以这么做。

一个解决的办法就是
由于大王小王可以代替任何牌，所以判断牌中最大值-最小值是否 < 5同时除了0 可以重复以外，其他均不可以重复。题解中的有一个图画的很好，借鉴一下

class Solution {
    public boolean isStraight(int[] nums) {
        Arrays.sort(nums);
        int min = nums[0];
        int max = nums[4];
        int count = 0;
        for(int i = 0; i < nums.length;i++){
            if(nums[i] == 0) {
                count++;
                continue;
            }
            //如果遇到了第一个不是0的数字 那么就是最小值
            min = nums[count];
            //第二个不是0 但是减去前一个 >1  或者是第二个不是0 但是和前一个相等
            if(i > 0 && nums[i] == nums[i-1] ){
                return false;
            }
        }
        return max - min < 5;
    }
}

62.圆圈中最后剩下的数字(√）

这个题其实还是蛮考验逻辑思维能力的，我有尝试用不断数下一个来解决这个题，但是确实逻辑思维不严谨，没有写出来。

思路一：动态规划
同时因为是只依赖于上一个状态的，所以并没有写出dp。但还是dp的思路罢了
看了看题解，发现这个题是一个约瑟夫环的问题，值得去学习一下！

人家就是这样的规律，至于为什么可以想到是用这样的规律来算，这我确实不知道啦。
感觉这种东西就是，事先已经知道了答案，只不过跟着答案反推。验证对不对。

class Solution {
     /**
     * 最后结束的时候 要删除的数字的是index=0 size = 1
     * 上一次的时候 要删除的数字的index = (上一个index + m) & 当前的数组长度
     * @param n
     * @param m
     * @return
     */
    public int lastRemaining(int n, int m) {
         //初始的状态 res = 0
        int res = 0;

        //删除了 n-1 个数字所以递推n-1次
        for(int i = 2; i<= n;i++){
            res = (res +m)%i;
        }

        //因为 我们假设的数组里面的数字是和下标一一对应的
        //也就是说数字的排列是从0开始的 所以下标是3 自然对应的数字也是3
        return res;
    }
}

63.股票中的最大利润（※）

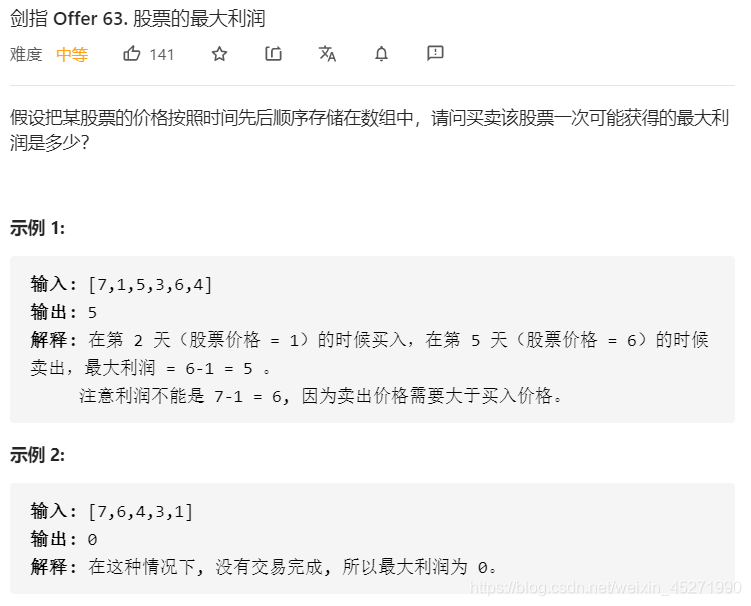
这个股票的问题，其实也是一系列的问题了。

推荐阅读
可能比较容易想到的就是找差值最大的，但是注意题里面卖出一定要比买入大。
注意这个题解里面是怎么到到避免卖出比买入小以及只可以买卖一次的情况！

状态表示
dp[i] [0] 当天不持股 可能由 前一天不持股 或者前一天持股今天卖出了转移
dp[i][1] 当天持股 可能由 前一天持股 或者是 由第一天不持股今天买入（只可以从0 第一天的状态开始
这里很重要 由第一天不持股 今天买入 保证了买入股票只能有一次 那么进而就保证了卖出股票只有一次。
同时初始化的时候买入股票设置成负值。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices == null || prices.length == 0) return 0;
        int[][]dp = new int[prices.length][2];

        //如果假设在第一天就买入 0 表示不持有股票 1 表示持有股票
        dp[0][0] = 0;
        dp[0][1] = -prices[0]; //将买入后价格设置位负数 就可以避免出现只看买入卖出的价格差值的情况 
        // 7 买入1 卖出 价格是-6 虽然7 和1 的差值最大

        for(int i = 1; i < prices.length;i++){

            //当天不持股  前一天不持股  前一天持股今天卖出了
            dp[i][0] = Math.max(dp[i-1][0] ,dp[i-1][1] + prices[i]);

            //当天持股 前一天持股 或者是 前一天不持股 当天买入（只可以从0 第一天的状态开始）
            //这里写成立dp[0][0] 就可以保证了股票只进行一次买入 
            //如果写dp[i-1][0] 而这个状态有可能是之前已经买入后卖出的状态 不能保证值买入一次
            dp[i][1]= Math.max(dp[i-1][1],dp[0][0]-prices[i]);
        }


        //最后一天一定是不持有股票的 为什么最大值是最后一个  而不是中间的某一个过程值呢？
        //因为如果中间的某一天如果卖出了股票 那么状态转移到下一天不持有股票的时候 这个值是会依次传递下去的。
        return dp[prices.length-1][0];

    }
}

64.求1+2+…+n（√）

思路一:递归

逻辑运算符的短路性质可以确定递归出口。

class Solution {
    public int sumNums(int n) {
        int sum = n;
        boolean flag = n > 0 && (sum += sumNums(n-1)) > 0;
        return sum;
    }
}

思路二：快速乘法
其实只需要知道一个东西1+2+⋯+n 等价于
* 1+2+…+n = n(n+1) / 2
对于除以 2 我们可以用右移操作符来模拟，那么等式变成了 n(n+1)>>1
那么对于 n(n+1) 方便就写成比如 A * B

其实就是将 B 二进制展开，如果 B 的二进制表示下第 i 位为 1，那么这一位对最后结果的贡献就是 A*(1<<i) ,即 A<< i。
我们遍历 B 二进制展开下的每一位，将所有贡献累加起来就是最后的答案，这个方法也被称作「俄罗斯农民乘法」
感觉有点大数相乘拆成进制 一个个的乘之后相加

那么如何转换成代码
本质就是B不断地的右移 判断是不是当前位是1
同时B右移的时候应当让A 左移一位 表示乘以2
如果当前B的这一位是1 那么ans 就加上A
否则ans就不需要变化了

class Solution {
    public int sumNums(int n) {
        int sum = 0;
        int A = n;
        int B = n+1;
        boolean flag ;

        flag = ((B & 1) >0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (sum += A) > 0;
        A <<= 1;
        B >>= 1;

        return sum >> 1; //除以2
    }
}

65. 不用加减法乘除做加法(※）

位运算的一个技巧性的题

位运算

两个数字进行按位异或得到的数字是当前位 （没有算进位）

两个数字进行按位与 之后左移1位 得到的是当前的进位

思路一：递归
递归的出口：在不断地递归中，如果进位是0 的话，那么直接返回当前位即可

class Solution {
    public int add(int a, int b) {
         if(b == 0){
            return a;
        }
        //异或的结果可以求出无进位的值
        //如果所有的进位是0 的话 那么就可以结束了
        int sum = a ^ b; //这里的sum 是 a和b 无进位的和
        int carry = (a & b) << 1;//算的是所有的进位

        //传递的参数就是当前位的和 和进制位
        return add(sum ,carry);
    }
}

思路二：迭代

class Solution {
    public int add(int a, int b) {
          while (b != 0) {
            int sum = a ^ b; //这里的sum 是 a和b 无进位的和
            int carry = (a & b) << 1;//算的是所有的进位
            
            a = sum;//然后让a = 无进位和
            b = carry; //b 等于进位 再次运算
        }
        //出现了b == 0，那么返回a即可
        return a;
        
    }
}

66.构建乘积数组（√）

技巧性的一个题。

如果可以使用除法，那就遍历一遍数组全部乘起来，然后用这个结果除以当前的数字。
当前b[i] 其实要做的就是知道它左边的乘积和 * 右边的乘积和

i 一次递增，那么左边的乘积是可以累成进行计算的，但是右边的乘积和是不断的缩小。但是又规定不可以使用除法，如果每一个都遍历，那么乘积是有重复的一部分的。所以可以采用左半边是从上往下，右半边从下往上计算的方式。

class Solution {
    public int[] constructArr(int[] a) {
        int[] b = new int[a.length];
        int temp = 1;
        //计算左边的乘积
        for(int i =0;i < a.length;i++){
            b[i] = temp;
            temp *= a[i];
        }
        
        //倒着计算右边的乘积
        //a.length -1 是最后一个
        temp = 1;
        for(int i= a.length-1;i >=0;i--){
            b[i] *= temp;
            temp *= a[i];
        }
        return b;
    }
}

67.把字符串转换成整数 （※）

做这个题可能会用到 一些知识
不可以向int变量直接赋值为最小的数字！

关于为什么不能直接向int变量赋值-2147483648，我搜索了一些资料，大致意思是说-2147483648是一个常量表达式而非常量，系统会把它分成两部分，即负号 - 和 数字 2147483648，因此会出现越界的情况。

处理一些越界的情况

• 如果当前的res 已经大于了最大值/10 那么不用说 肯定会越界
• 如果当前的res 等于最大值/10 这个时候去判断当前获取到的char 如果char > '7’也就视为越界
  

所以说 Integer.MAX_VALUE/10 就是关键的判断点。

class Solution {
    public int strToInt(String str) {
        int sign = 1;
        int res = 0;
        int bound = Integer.MAX_VALUE/10;
        if(str == null) return 0;

       //去除空格 之后判断字符
        str = str.trim();
        if (str.length() == 0) return 0;
        
        //首先找到第一个非空格
        int index = 0;
        char ch = str.charAt(index);
        //第一个非空格如果是字符直接返回0
        if(ch >= 'a' && ch <= 'z'){
            return 0;
        }
        if(ch =='-'){
            sign = -1;//表示是一个负数
            index++;
        }
        if(ch == '+') index++;
        for(int i = index;i < str.length();i++){
            char temp = str.charAt(i);
            if(temp < '0'||temp > '9') break;
            //在这里需要处理一些越界的情况！！

            //如果还没有乘以10 已经比大 说明会越界
            if(res > bound || res == bound && temp > '7'){
                return  sign == 1? Integer.MAX_VALUE:Integer.MIN_VALUE;
            }


            res =  (temp-'0') + ( res * 10);
        }
        return  res*sign;
    }
}

68-I.二叉搜索树的最近公共祖先（※）

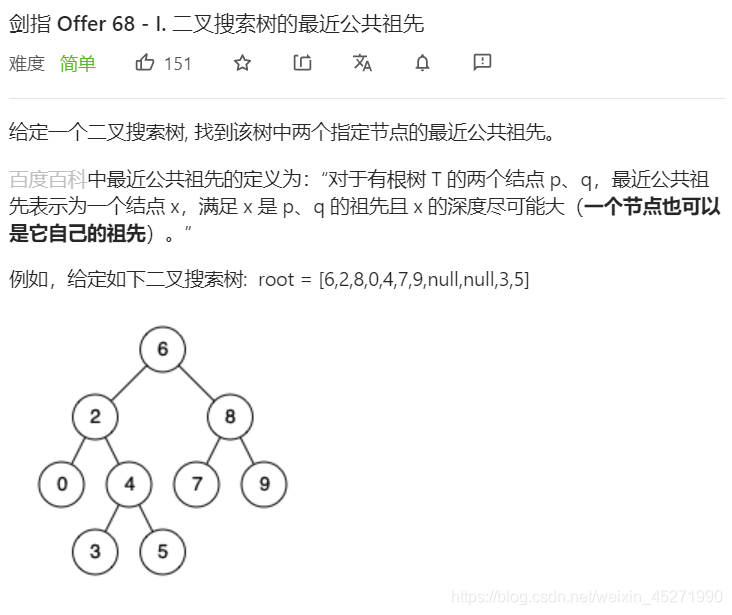
若 root 是 p,q的 最近公共祖先 ，则只可能为以下情况之一：

p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
p = root 且 q 在 root的左或右子树中；
q = root 且 p 在 root的左或右子树中；

思路一：递归

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
         if(p.val > root.val && q.val > root.val){
            return lowestCommonAncestor(root.right,p,q);
        }else if(p.val < root.val && q.val < root.val){
            return lowestCommonAncestor(root.left,p,q);
        }else {
            return root;
        }
    }
}

思路二：迭代

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
          while (root != null){
            if(p.val > root.val && q.val > root.val){ //都在右子树
                root = root.right;
            }else if(p.val < root.val && q.val < root.val){ //都在左子树
                root = root.left;
            }else { //分布在左右子树
               break;
            }
        }
        return root;
    }
}

68-II. 二叉树的最近公共祖先（※※）

还是和上面一样，若 root 是 p,q的 最近公共祖先 ，则只可能为以下情况之一：
p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）
p = root 且 q 在 root的左或右子树中；
q = root 且 p 在 root的左或右子树中；

那么我们可以采用先序遍历的方式来做。
遍历的终止条件

• root == null return null 说明遍历的这条路径上面没有 p 或者 q 那么
• 如果找了p 或者 q 就可以返回 这个结点

开启递归左子节点，返回值记为 left ；
开启递归右子节点，返回值记为 right ；

对于最后的处理情况
由于是从root 的根节点 开始遍历
最后需要保存对于left 和 right的遍历结果

left 和right 都为null 说明两个结点都不存在 （题目已知都存在了）
left 和 right 都不为null 说明分布在root的两侧返回root
left 不为null 返回 递归left 获得的值
同理 right 不为null 返回递归right 获得的值

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //说明root的左右结点中不存在
        return preOrder(root,p,q);
    }

    private TreeNode preOrder(TreeNode root, TreeNode p, TreeNode q) {
         //递归的终止条件
        if(root == null) return null;//这里表示先序遍历一直没有找到p或者q
        if(root == p || root == q) return root;

        TreeNode left = preOrder(root.left,p,q);
        TreeNode right = preOrder(root.right,p,q);


        //分析情况
        //如果left 不等于null 并且right ！= null 那么 返回root 说在在它的左和右子树中分别找到了
        //如果left==null  right ！= null  || left == null right != null  也返回不为null

       if(left != null && right != null) return root;
       if(left != null) return left;
       return right;
    } 
}

※标注的题目是个人认为和比较常规的锻炼算法思维的题目，需要多次练习，是代码的硬实力。
√是一些算法技巧相关的，这种就属于是多做题，做多了可能就会想到。