C语言函数递归

1.含义

函数递归（recursion），是指函数调用自身的编程技巧。

2.必要条件

函数递归存在两个必要条件：
1. 设定限制条件，当满足这个条件时，递归不再继续；
2. 每次递归调用之后越来越接近限制条件。
调用递归函数的目的是为了求解一个复杂问题，但是函数必须先知道问题在最简单情况下的解（也就是基线条件），调用递归函数时，函数将问题分为两部分：一部分是函数已经知道答案，另一部分是函数尚未知道答案，为了保证递归求解的可行性，后一部分问题必须与原问题类似，且是原始问题的一个更小规模的版本，这些逐渐变小的问题必须收敛于基线条件。由此可见，函数递归的核心思想是：以大化小。

3.执行过程

由上所述，在执行函数递归的过程中，函数每次会用更小规模的原始问题调用自身，这些逐渐变小的问题最终会收敛于基线条件。程序执行到这里时，递归函数识别出基线条件时，将基线条件的解返回到调用它的上一个函数，接下来就是一连串的直线式返回操作，直到最终由函数的原始调用将原始问题返回给其主调函数。

例题：顺序打印其每个位数上的数字

void print(unsigned int n)//void表示无返回值
{
	if (n > 9)
	{
		print(n / 10);
	}
	printf("%d ", n % 10);
}
int main()
{
	unsigned int num = 0;
	printf("请输入一个数:>");
	scanf("%d", &num);
	print(num);
}

假设num=1234,执行函print（1234），内存分配新的栈
n=1234>9，执行print（123），递归进栈；
n=123>9，执行print(12) ， 递归进栈；
n=12>9，执行print（1）， 递归进栈；
n=1<9, 不再分配新的栈，开始出栈：

n=1, n%10=1,打印1；
n=12， n%10=2，打印2；
n=123, n%10=3,打印3；
n=1234 ,n%10=4,打印4。
最开始学习递归函数时，为了便于理解，习惯画出函数调用时的压栈出栈示例图
思路：

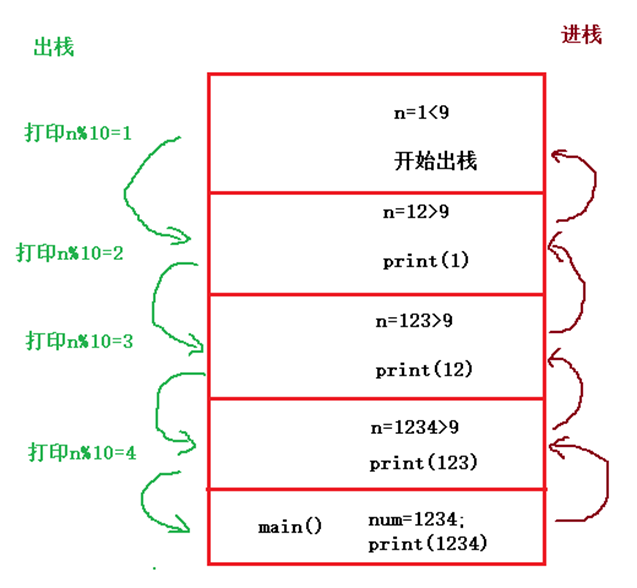
图1 例题对应的栈区示意图

4.递归和迭代的区别

• 递归和迭代都分别以一种控制结构为基础：迭代基于循环语句，而递归基于选择语句；
• 递归和迭代都需要循环地执行：迭代是使用一个循环语句，而递归通过重复地调用函数来实现循环；
• 递归和迭代都需要进行终止测试：当循环继续条件为假时，迭代结束；而递归是在遇到基线条件时终止；
• 递归和迭代都可能会出现无限执行的情况：若一个循环继续条件永远不会为假，则发生无限循环；如果递归执行产生的新问题不是逐渐收敛于基线条件，也导致无限递归；
• 递归需要不断地执行函数调用机制，因此会产生很大的函数调用开销，从而在处理器的时间和存储器的空间两方面付出很大的代价。