前言
这里笔者了解相对较为薄弱,参考了胡凡老师编写的《算法笔记》一书的第十章,这本书是学习算法的优秀书籍,适合学习过c++语言但是对算法理解不深的同学,推荐给大家。
1.图的定义和相关术语
什么是图?其实就是类似地图的东西。
图一般而言可以分为顶点和边,每条边的两个端点是顶点。如下图:

图可以分为无向图和有向图,简单概括起来就是通过边是否有箭头标明方向来区分。有向图往往是单向的,即从A可以到B,但从B到A不一定存在边,而无向图是双向的,从A可以到B,从B一定可以到A。
顶点的度是指该顶点相连的边的条数。特别是对于有向图来说,出边的条数为出度,入边的条数为入度。
顶点和边都有一定的属性,称为权值,顶点的权值称为点权,边的权值称为边权。可以根据实际情况设定,例如点权可以是城市中资源的数量,边权可以是两个城市间来往所需要的时间或者长度。
2.图的存储
一般来说,图可以用两种方法存储,邻接矩阵和邻接表。
2.1 邻接矩阵
设某个图有N-1个顶点,那么可以用二维数组G[N][N]来表示图的顶点标号,如果G[i][j]是1则表明存在从i到j的边,为0则表示不存在边,这个二维矩阵称为邻接矩阵。此外,如果存在边权,那么可以让这个值为边权,对不存在的边让其等于-1或者无穷大均可。

注意:虽然邻接矩阵很容易构造,但是由于需要一个二维数组,如果顶点数目太大往往会超时或者超出内存,因此对于不超过1000个顶点的题目适用,再大就不能用了。
2.2 邻接表
设图G(V,E)的顶点编号为0,1,2,3…N-1,每个顶点都可能有若干条边,如果把同一个顶点的所有出边放在一个列表中,那么N个顶点就会有N个列表,这N个列表就叫做G的邻接表,记为Adj[N],其中Adj[i]存放顶点i的所有出边构成的列表。这个列表可以用链表实现。
例如上面的图,可以构造成下列图示的链表:

我们利用vector来实现邻接表。
我们使用vector构造一个vector的数组Adj[N],其中N为顶点个数,这样每个Adj[i]都是一个变长的数组,使得存储空间只与图的边数有关。
如果邻接表只存放每条边的终点编号,而不存放边权,则vector的元素类型可以直接定义为int类型;
vector<int> Adj[N];
如果我们要添加一条从1到3的有向边,只需要在Adj[1]中添加编号3即可。
Adj[1].push_back(3);
当然,如果要同时存放编号和边权,我们可以用结构体;
struct Node{
int v;//编号
int w;//边权
};
这样定义Adj时,就需要将int换为Node型;
vector<Node> Adj[N];
如果要添加边需要:
Node temp;
temp.v =3;
temp.w =4;
Adj[1].push_back(temp);
3.图的遍历
3.1 深度优先搜索DFS
深度遍历时,要求沿着路径到不能再前进时才能退回到最近的岔路口。
两个概念:
连通分量:无向图中如果任意两个顶点都连通,则称图G是连通图;否则,称为非连通图,称其中的极大连通子图为连通分量。
强连通分量:有向图中如果任意两个顶点可以互相到达,则图为强连通图,否贼,其极大连通子图为强连通分量。
我们将两者统称为连通块。
可以想象,如果要遍历整个图,就需要对所有的连通块进行遍历。所以DFS遍历图的基本思路就是将经过的顶点设置为已访问,在下次递归碰到时就不再处理,知道整个图都被访问。
下面是一份伪代码,提供基本思路;
DFS(u) //访问某个顶点u
{
vis[u] = true; //设置u已被访问
for(从u出发可达的所有顶点v)
{
if(vis[v]==false) DFS(v);//v未被访问时才访问
}
}
DFSTrave(G)//遍历图G
{
for(G的所有顶点u)
{
if(vis[u]==false) DFS(u);
}
}
基于此,我们可以写出邻接矩阵和邻接表的代码:
邻接矩阵:
const MAXV = 1000;
const INF = 1000000000;
int n, G[MAXV][MAXV];
bool vis[MAXV]={false};
void DFS(int u,int depth)
{
vis[u]=true;
//如果需要对u进行一些操作可以在这里进行
//下面对所有从u出发能到达的分支顶点进行枚举
if(int v=0;v<n;v++)
{
if(vis[v]==false && G[u][v]!= INF)
{
DFS(v,depth+1);
}
}
}
void DFSTravle()
{
for(int u=0;u<n;u++)
{
if(vis[u]==false)
{
DFS(u,1);
}
}
}
邻接表:
vector<int> Adj[MAXV];
int n;
bool vis[MAXV]={false};
void DFS(int u,int depth)
{
vis[u] =true;
for(int i=0;i<Adj[u].size();i++)
{
int v = Adj[u][i];
if(vis[v]==false)
{
DFS(v,depth+1);
}
}
}
void DFSTrave()
{
for(int u=0;u<n;u++)
{
if(vis[u]==false)
{
DFS(u,1);
}
}
}
3.2 广度优先搜索BFS
同DFS,需要对单个连通块进行遍历,如果要遍历整个图,就需要对所有连通块遍历。
这里的思路是建立队列,把初始顶点加入队列,此后每次都取出队首顶点进行访问,并把从该点厨房可以达到的未曾入队的的顶点全部入队,直到队列为空。
按照这个思路,伪代码如下:
BFS(u)
{
queue q;
将u入队;
inq[u] = true;
while(q非空)
{
取出q队首元素u进行访问
for(从u出发可达的全部顶点v)
{
if(inq[v]==false)
{
将v入队;
inq[v] = true;
}
}
}
}
BFSTrave(G)
{
for(G的顶点u)
{
if(inq[u]==false)
{
BFS(u);
}
}
}
邻接矩阵:
const MAXV=1000;
const INF = 10000000;
int n,G[MAXV][MAXV];
bool inq[MAXV]={false};
void BFS(int u)
{
queue<int>q;
q.push(u);
inq[u]=true;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int v=0;v<n;v++)
{
if(inq[v]==false&&G[u][v]!=INF)
{
q.push(v);
inq[v]=true;
}
}
}
}
void BFSTrave()
{
for(int u=0;u<n;u++)
{
if(inq[u]==false)
{
BFS(q);
}
}
}
邻接表:
const MAXV=1000;
const INF = 10000000;
vector<int> Adj[MAXV];
bool inq[MAXV]={false};
void BFS(int u)
{
queue<int>q;
q.push(u);
inq[u]==true;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<Adj[u].size();i++)
{
int v=Adj[u][i];
if(inq[v]==false)
{
q.push(v);
inq[v]=true;
}
}
}
}
void BFSTrave()
{
for(int u=0;u<n;u++)
{
if(inq[u]==false)
{
BFS(q);
}
}
}
4.拓扑排序
4.1有向无环图
拓扑结构的基础是有向无环图,正如字面所示,是有方向,但不形成一个环的图。
4.2 拓扑排序
拓扑排序的定义很抽象,是将有向无环图的所有顶点形成线性序列的排序,使得任意两个顶点之间,如果存在u->v,那么u一定在v前面。
具体举例来说就是,教务系统排课,要求在学习复变函数之前必须学习高等代数和解析几何,那么在给学生排课程表时,就必须先安排高等代数和解析几何的课程,很多课程之间都存在这样的前驱和后继关系,那么用拓扑排序就可以得到合理的排课顺序。
伪代码如下:
const maxv=1000;
int n,m,inDegree[maxv];//顶点数和入度
vector<int> G[maxv];
//拓扑排序
bool topologicalSort()
{
int num=0;
queue<int> q;
for(int i=0;i<n;i++)
{
if(inDegree[i]==0)
{
q.push(i);
}
}
while(!q.empty())
{
int u=q.front();
//取队首顶点
q.pop;
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
inDegree[v]--;
if(inDegree[v]==0)
{
q.push(v);
}
}
G[u].clear();//情况顶点u的出边
num++;//
}
if(num==n) return true;
else return false;//如果顶点数小于n那么拓扑排序失败
}
5.关键路径
5.1 AOV网和AOE网
顶点活动网(AOV)是指用顶点表示活动,而用边集表示活动间优先关系的有向图。显然图中不存在环。
边活动网(AOE)是指用带权值的边表示活动,而顶点表示事件的有向图,其中边权表示活动完成需要的时间。
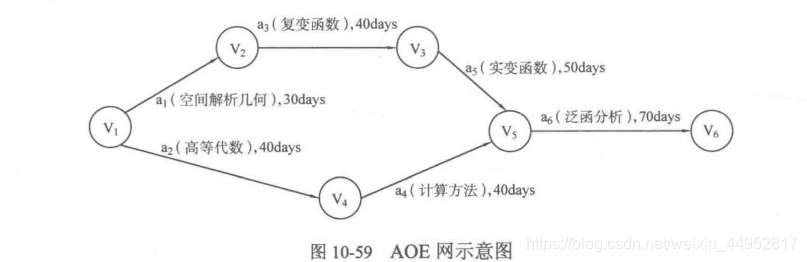
一般来说,AOE网用来表示一个工程的进行过程,而工程常常可以分为若干子工程(活动),显然AOE网络不应该有环。对工程来说总会有一个起始时刻和结束时刻,因此AOV网一般只有一个源点(入度为零)和一个汇点(出度为零),不过实际上即便有多个源点和汇点,仍然可以转换为一个源点和一个汇点,也就是添加超级汇点和超级源点,从超级源点开始,连接所有入度为零的点,从所有出度为零的点出发,连接到超级汇点上,其边的权重均为0。
基于此,我们需要解决的问题有:
- 工程起始到结束需要多少时间
- 那条路径上的活动是影响整个工程的关键
如上图所示,由于完成a1,a3,a5共需要120天,因此在a2完成的前提下,有40天的弹性时间,只需要在41-88天开始学习a4的计算方法就可以在a5实变函数完成前完成a4,而能够进入学习a6,显然a1,a3,a5,a6这4个活动很关键,因此推迟其中的任意一个都会导致工程完成时间更长。
AOE网中的最长路径被称为关键路径,关键路径上的活动叫做关键活动。
5.2 最长路径
最长路径问题可以等效为最短路径问题,至于具体怎么求会在后面详细解读,我们需要做的就是在最短路径的基础上让权值变为负数,就可以求得最长路径。
5.3 关键路径
由于AOE网络实际是有向无环图,而关键路径是最长路径,因此求关键路径也就是求有向无环图中最长路径。
由于关键活动是不允许拖延的活动,因此这些活动的最早开始时间必须等于最晚开始时间。因此可以设置数组e和l,e表示最早开始时间,l表示最晚开始时间,可以通过判断e[i] r[i]是否相等来判断i是否是关键活动。
如何求e[],r[]呢?

事件Vi的最早发生时间等于从源点V1到Vi的最长路径的长度
事件Vi允许的最晚发生时间等于最早完成时间减去从vi到vn的最长路径长度
设活动ak=<vi,vj>,活动最早开始时间等于vi的最早发生时间,而最晚开始时间等于vj-ak的权值。例如:
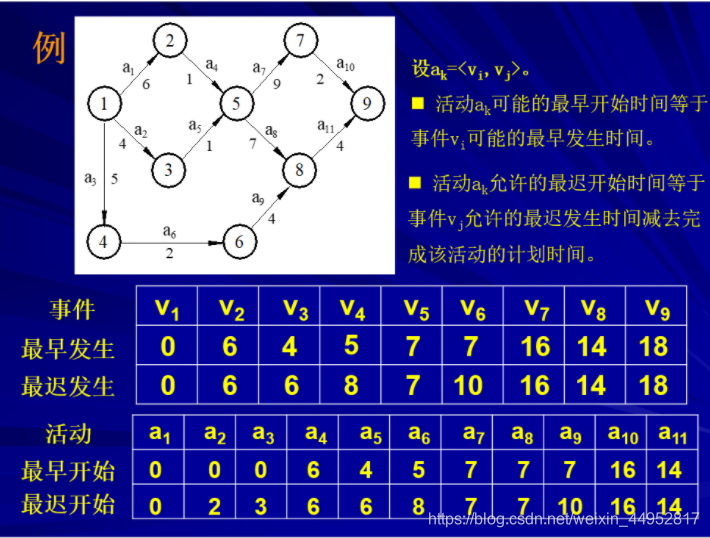
只要活动的最早开始时间等于最迟开始时间,那么就能得到关键路径。





 本文介绍了图的定义、术语及其存储方式,包括邻接矩阵和邻接表。接着讲解了深度优先搜索(DFS)和广度优先搜索(BFS)的原理及其实现,并探讨了这两种遍历方法在图遍历中的应用。最后,文章讨论了有向无环图(DAG)的拓扑排序和关键路径的概念,以及它们在工程管理和项目计划中的重要性。
本文介绍了图的定义、术语及其存储方式,包括邻接矩阵和邻接表。接着讲解了深度优先搜索(DFS)和广度优先搜索(BFS)的原理及其实现,并探讨了这两种遍历方法在图遍历中的应用。最后,文章讨论了有向无环图(DAG)的拓扑排序和关键路径的概念,以及它们在工程管理和项目计划中的重要性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








