关于深度学习人工智能模型的探讨（五）（7）

5.7 盖世英雄ℵ 2（阿列夫2）

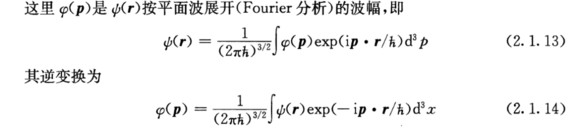
相信很多朋友见到这两个傅立叶变换的式子都不陌生，但是却很难亲切，因为这两个式子很容易让人迷糊晕菜。每一个位移值都由无穷多个复动量构成、而每一个复动量值又由无穷多个复位移构成。就像在两个对照的镜子里，你中有我、我中有你，层层嵌套、无穷无尽。第一直觉，“非独立二元复指数”，貌似多重旋量（虚数i）的高阶张量。心里不停的嘀咕，莫非这是多重旋量层层嵌套的∞ ^∞ ，即无穷大的无穷大次方维度空间？莫非，这背后里隐含一个阿列夫2维特征属性的张量空间么？？？

[命题] 以相互正交的量子本征态exp(ipr)函数为元素的集合的势为阿列夫2

[上面命题有点拗口，大意是相互正交的exp(ipr)函数一共有阿列夫2 个，即以exp(ipr)为特征基的完备系统是阿列夫2 维度空间]

下面让我们一步一步粗略探讨，看看相互正交的exp(ipr)函数究竟有多少个？

（1）当exp(ipx)函数的变量整数取值时，相互正交exp(ipx)函数的个数为阿列夫0

【 证明一：

取位移值xm和xn ，其中m、n为整数

则：∫exp(ip)^xn exp(-ip)^xm dp

相当于计算两个exp(ipx）的乘积

又由于exp(ipx）可以转换为三角函数：

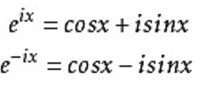
所以exp(ipx)的正交性，对应于三角函数的正交关系

即：m不等于n时的exp(ip xm)和exp(ip xn)两两内积为0

所以，两两不同的exp(ip)^xn 和exp(ip)^xm正交

又因为， 整数变量xn与函数exp(ip)^xn 一一对应，所以不同整数取值的exp(ip)^xn函数个数为阿列夫0

即，不同整数取值的两两正交的exp(ip)^xn 函数个数为阿列夫0 阶无穷大】

【证明二：

因为

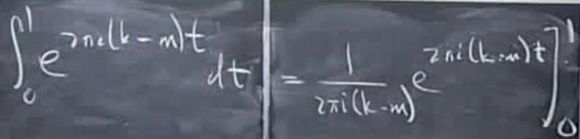
根据欧拉公式：

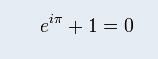
可知，整数不同取值的 k、m的exp(ikt)函数 和exp(imt）函数两两正交

又因为， 整数变量k与函数exp(ikt)对应，所以不同整数取值的exp(ikt)函数个数为阿列夫0

即，不同整数取值的两两正交的exp(ikt) 函数个数为阿列夫0 】

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

（2）当ex