Hopfield神经网络与受限波尔兹曼机

神经网络可分为两大类：

• 一类是多层神经网络、卷积神经网络：可用于模式识别
• 另一类是相互连接型网络：可通过联想记忆去除输入数据中的噪声。

深度学习目录：

1. 自适应线性单元 (Widrow and Hoff, 1960)
2. 神经认知机 (Fukushima, 1980)
3. GPU-加速 卷积网络 (Chellapilla et al., 2006)
4. 深度玻尔兹曼机 (Salakhutdinov and Hinton, 2009a)
5. 无监督卷积网络 (Jarrett et al., 2009b)
6. GPU-加速 多层感知机 (Ciresan et al., 2010)
7. 分布式自编码器 (Le et al., 2012)
8. Multi-GPU 卷积网络 (Krizhevsky et al., 2012a)
9. COTS HPC 无监督卷积网络 (Coates et al., 2013)
10. GoogLeNet (Szegedy et al., 2014a)

Hopfield神经网络 HNN(Hopfield Neural Network)

1982年Hopfield 提出了Hopfield神经网络，是最典型的相互连接型神经网络。

首先我们来看看脑部神经元结构图

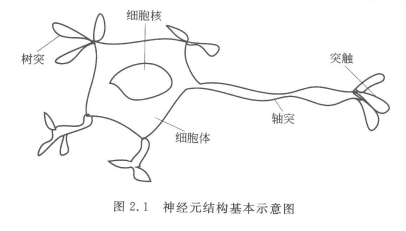
生物神经元和人工神经元的对照关系

Hopfield神经网络是一种递归神经网络，从输出到输入均有反馈连接，每一个神经元跟所有其他神经元相互连接，又称为全互联网络。
我们根据如上形式，将所有神经元之间两两连接，形成了全互联网络

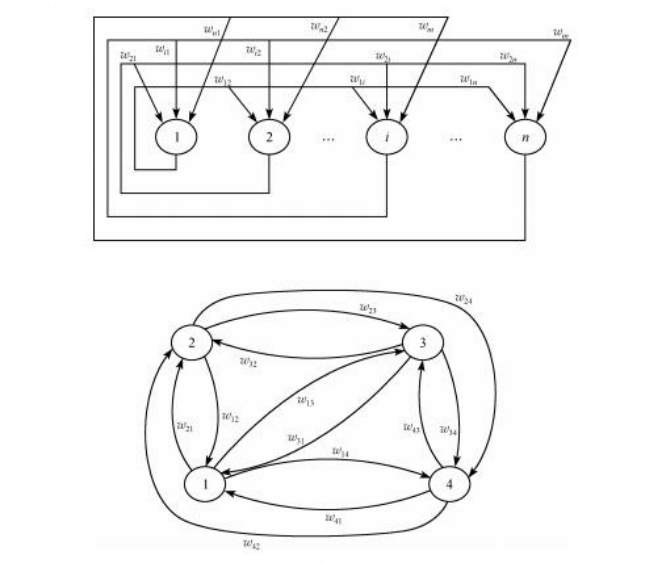
Hopfield最早提出的网络是二值神经网络，各神经元的激励函数为阶跃函数或双极值函数,神经元的输入、输出只取 $(0，1)$ 或者 $(-1，1)$ ，所以也称为离散型Hopfield神经网络DHNN（Discrete Hopfiled Neural Network）

离散Hopfield神经网络DHNN是一个单层网络，有n个神经元节点，每个神经元的输出均接到其它神经元的输入。各节点没有自反馈。每个节点都可处于一种可能的状态（1或－1），即当该神经元所受的刺激超过其阀值时，神经元就处于一种状态（比如1），否则神经元就始终处于另一状态（比如－1）。

构建Hopfield神经网络

首先，构建Hopfield神经网络需要提供要求记忆的二进制网络，如：

a=np.array([[0,0,1,1,0,0],
            [0,0,1,1,0,0],
            [1,1,1,1,1,1],
            [1,1,1,1,1,1],
            [0,0,1,1,0,0],
            [0,0,1,1,0,0]])

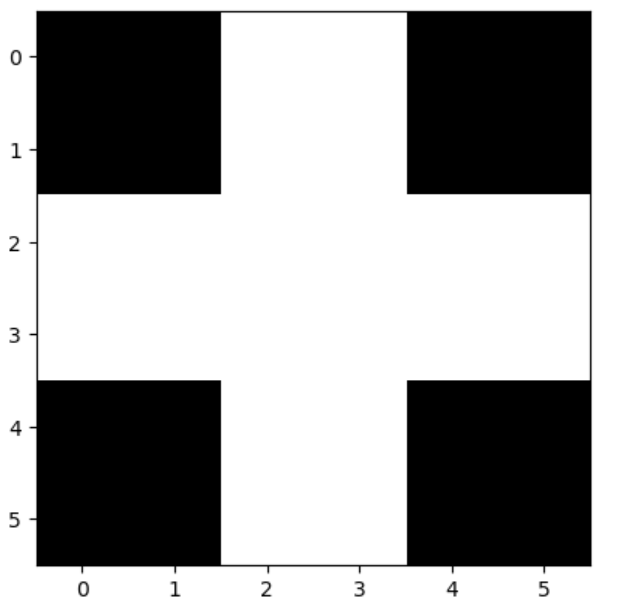
设置神经网络的网络权值

因为网络共有$6\ast 6=36$个结点。故神经网络连接需要$35\ast 35$个（自身与自身不连接）。

我们首先将二维图像展开成为一层

array_a=a.flatten()

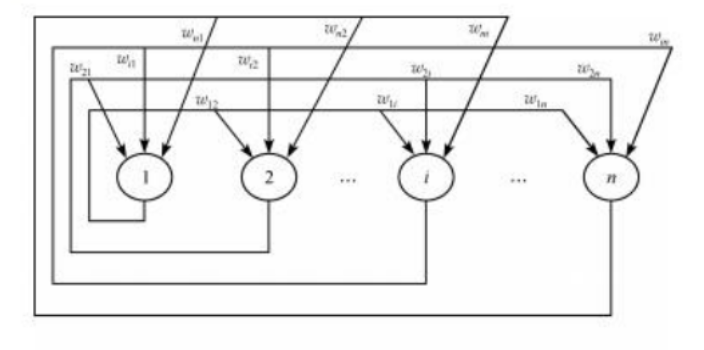
其次，设置连接权值。

我们已知Hopfield神经网络为二值神经网络，值为0或1。

设：
当 a [ i ] 为 0 ， a [ j ] 为 1 时 , 权值 w i j 为 − 1 当 a [ i ] 为 0 ， a [ j ] 为 0 时 , 权值 w i j 为 1 且 w j i = w i j 即：俩结点值相同权值为 1 ，结点不同权值为 0 当 a[i]为0，a[j]为1时,权值w_{ij}为-1\\ \quad\\ 当 a[i]为0，a[j]为0时,权值w_{ij}为1\\ \quad\\ 且w_{ji} = w_{ij}\\ 即：俩结点值相同权值为1，结点不同权值为0 当a[i]为0，a[j]为1时,权值wij​为−1当a[i]为0，a[j]为0时,权值wij​为1且wji​=w