决策树ID3与C4.5介绍*_c4.5的评价指标-优快云博客

学习自：link

决策树理论

主要介绍ID3、C4.5、CART。

信息论基础

熵：度量事务的不确定性。
随机变量X的熵：

其中 $p_i$ 指的是随机变量X的概率分布。log一般取2为底。
实际上，信息熵是X每个取值发生后所带来的信息的期望。

联合熵： 两个变量X，Y的联合熵：

条件熵： 类似于条件概率，度量了知道Y以后，X的不确定性。（这里已知Y的意思就是，Y的取值已经固定）

$H (X) - H (X ∣ Y)$ 就表示，已知Y后，X的不确定性减少了多少。其实这就是互信息。

互信息： 衡量随机变量之间相互依赖程度的度量。

代入概率展开得计算公式：

用一张图形象表示信息熵与互信息的关系：
当两个随机变量相同时，互信息最大：

图像上表现在两个椭圆重合，公式上表现在 $H (X ∣ X) = 0$ .

ID3将互信息作为评价指标

实际上，互信息在决策树中称为信息增益。
决策树中，数据集的混乱程度就是熵，分支过程中，剩下的数据混乱程度应该越来越小。
这里我们举一个信息增益计算的具体的例子。比如我们有15个样本D，输出为0或者1。其中有9个输出为1， 6个输出为0。样本中有个特征A，取值为A1，A2和A3。在取值为A1的样本的输出中，有3个输出为1， 2个输出为0，取值为A2的样本输出中,2个输出为1,3个输出为0，在取值为A3的样本中，4个输出为1，1个输出为0.
在这里插入图片描述

算法过程

在这里插入图片描述

（2）中：所有1）样本在属性上的取值相同，其实与2）当前属性集为空本质上一样，因为1）如果继续划分，所有的样本都会沿着一条支线往下，到最后属性用完了，还是不能将样本划分清除，也就是2）。

ID3的不足

没有考虑到特征是连续值的情况。（因为ID3在分出子树的时候，考虑的是这个特征的所有“取值”，连续属性显然这个“取值”是无穷个）
评价指标/划分选择的依据 ---- 信息增益有明显缺点：相同条件下，取值多的特征比取值少的特征信息增益大。（书上举了一个用样本编号当作一列属性，计算信息增益的例子，显然，每个样本都有一个编号，依次划分出来的子集们“纯度是非常（最）高的”）。
ID3算法对缺失值没有做考虑。
没有考虑过拟合的问题。

决策树C4.5对以上问题做了一些改进。

C4.5的改进

问题1. 处理连续特征：

主要策略：连续特征离散化。
样本中特征A的连续取值有m个，为 $a_1,a_2,...,a_m$ ，取相邻两个值的平均数，得到m-1个划分点，第i个划分点记为 $T_i=\frac{a_i+a_{i+1}}{2}$ 。对于这m-1个点，还要选择信息增益最大的的点作为该连续特征的二元离散分类点。
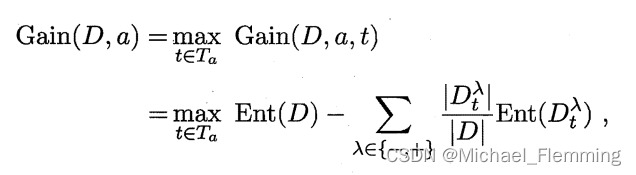
在这里插入图片描述

所以，**连续特征的节点划分比离散特征多了一步。**连续特征的划分 需要先算出余下每个连续特征的二元离散分类点，再根据这种二元划分，算出余下每个特征的信息增益。离散特征的划分，只有计算信息增益那一步。
注意：如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。（也就是根据该连续特征划分节点后，不需要把该特征在特征集合中删除）

问题2. 信息增益偏好取值多的特征：

用信息 “增益率（gain ratio）”来代替信息增益划分属性。
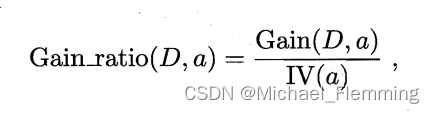
在这里插入图片描述
其中，

是属性a的“固有值”。属性a的取值越多，IV(a)越大。
书上强调了：，增益率准则对可取值数目较少的属性有所偏好?因此 C4.5 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式。先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

问题3. 缺失值：

这就涉及到两个子问题：1）如何在属性值缺失的情况下进行属性划分选择？
2）给定划分属性，若样本在该属性上值缺失，如何划分样本？

令 $\tilde{D}$ 表示 $D$ 中在属性a上没有缺失值的样本子集。对每一个样本赋予一个权重，定义：

推广信息增益的计算公式为：

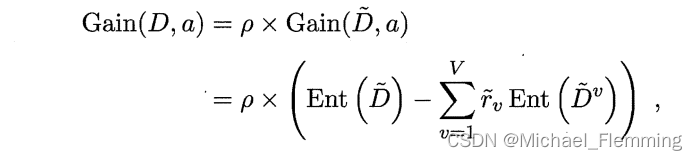
其实就是 利用未缺失值的样本来替代整体样本，通过乘以权重的手段来降低这种替代的“不精确性”。
如果划分属性已知，但是样本x在属性a上的取值缺失。解决办法是：将样本x划入所有的子节点，但是在不同的子节点上给样本赋予不同的权重，比如可以是 $\tilde{r}_v \cdot w_x$ ；直观的看，这就是让同一个样本以不同的概率划分到不同的子节点中去。