本文详细介绍了两种经典的排序算法——快速排序和希尔排序。快速排序由东尼·霍尔提出，通过选取轴点元素并不断分割序列实现排序，平均时间复杂度为O(nlogn)。希尔排序则是通过设定步长序列对序列进行多列排序，最终达到整体有序，其时间复杂度取决于步长序列。文章还探讨了两种排序算法的时间复杂度和稳定性，并提供了相应的代码实现。
1. 快速排序（Quick Sort）
1960年由东尼·霍尔发现。
1.1 执行流程
- 从序列中选择一个轴点元素
pivot；
例如：这里选择是索引为 0 的元素进行比较：
- 利用pivot将序列分割成两个子序列；- 将小于
piovt的元素放到piovt前面（左侧）； - 将大于
piovt的元素放到piovt后面 （右侧）； - 等于
pivot的左右都可以。
- 将小于
轴点元素 6 将序列分为左右两份：
- 重复上两步操作，直到不能再进行分割（子序列剩下一个元素 ）。
重复进行分割：
直到序列只剩下一个元素，排序完毕：
1.2 轴点构造
- 序列：
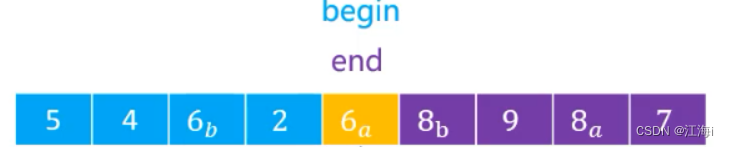
begin表示序列的第一个元素，end是序列的最后一个元素。
-
备份：这里将
begin位置的元素作为轴点备份。
-
比较和挪动：使用轴点元素与序列中其它元素进行比较：并不是一味的从
end或者begin方向比较，如果修改了哪个方向的元素，再从那个方向开始比较。1.与
end位置元素比较，7 > 6 ：位置元素不变，end指向上一个元素。
-
再与
end位置元素比较，5 < 6：将 5 放到begin位置，begin指向下一个元素。
-
与
begin位置元素比较，8 > 6，覆盖掉当前end位置元素，end指向上一个元素。
-
循环比较，直到子序列中元素数量为一，即
end == beign，再将备份的元素赋值过来。
-
此时：
begin或者end位置的元素就是轴点元素。
1.3 代码实现
/**
* @Description 快速排序实现
* @date 2022/5/7 9:13
*/
public class QuickSort<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
sort(0,arr.length);
}
/**
* 对 [begin, end) 范围内元素进行快速排序
* @param begin
* @param end
*/
private void sort(int begin, int end){
if (end - begin < 2) return;
// 确定轴点位置
int mid = pivot(begin, end);
// 对子序列进行快速排序
sort(begin,mid);
sort(mid + 1, end);
}
/**
* 构造 [begin, end) 范围的轴点元素
* @param begin
* @param end
* @return 轴点元素位置
*/
private int pivot(int begin, int end){
// 随机一个元素与begin位置元素交换
swap(begin, begin + (int)(Math.random() * (end - begin)));
// 备份目标元素
T pivot = arr[begin];
// 让 end 指向最后一个元素的索引
end--;
while (begin < end){
while (begin < end) {
if (cmp(pivot, arr[end]) < 0) {
end--;
} else {
arr[begin] = arr[end];
begin++;
break; // 跳出转向
}
}
while (begin < end) {
if (cmp(pivot, arr[begin]) > 0) {
begin++;
} else {
arr[end] = arr[begin];
end--;
break; // 跳出转向
}
}
}
// 重新赋值备份元素
arr[begin] = pivot;
// 轴点元素位置
return begin;
}
}
1.4 时间复杂度和空间复杂度
-
最好情况下（包括平均时间复杂度），序列的左右两端元素数量分布均匀时间复杂度为
O(nlogn)； -
最坏情况下，序列的左右两端元素数量分布极不均匀时间复杂度为
O(n^2)； -
降低最坏情况的出现概率，可以随机选取轴点元素：
// 随机一个元素与begin位置元素交换 swap(begin, begin + (int)(Math.random() * (end - begin))); -
空间复杂度为
O(logn)； -
属于不稳定排序。
2. 希尔排序（Shell Sort）
把序列看作一个矩阵，分成 m 列，逐列进行排序。
- 分成 m 列之后，m 从某个整数逐渐减为一；
- 当 m 为一时，整个序列将变得有序。
- 矩阵的列数取决于步长序列；
- 也被称为递减增量排序。
2.1 执行流程
希尔本人给出的步长序列为：n / 2k，当
n = 16时，步长序列是{1, 2, 4, 8}。
-
原始数组
-
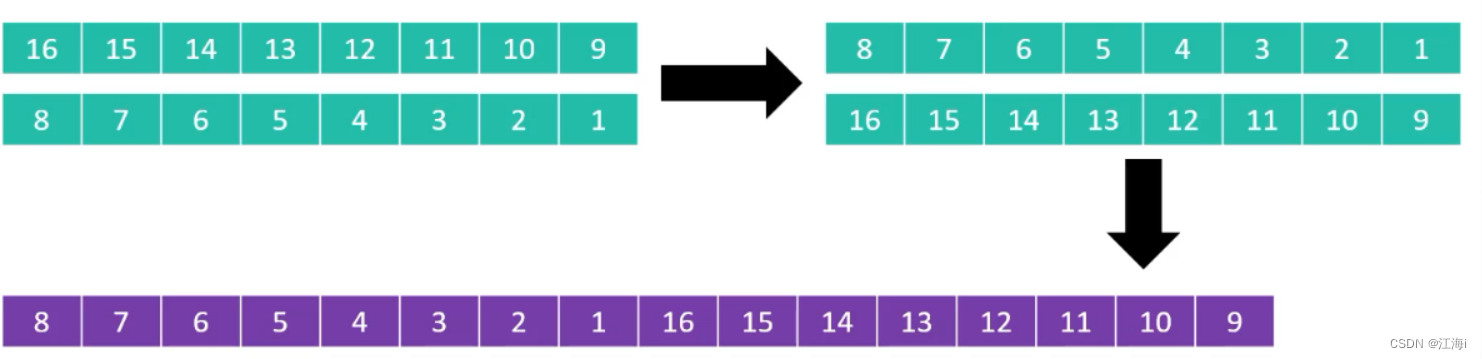
分成八列进行排序：先分成八列，在按照从小到大分别排序。
-
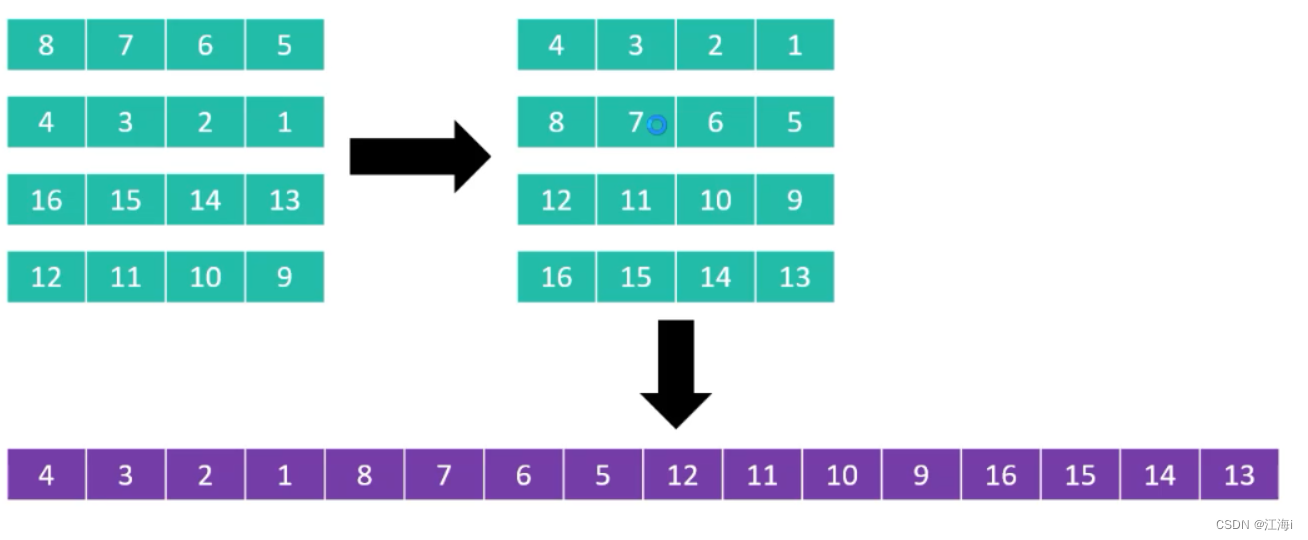
分成四列进行排序：
-
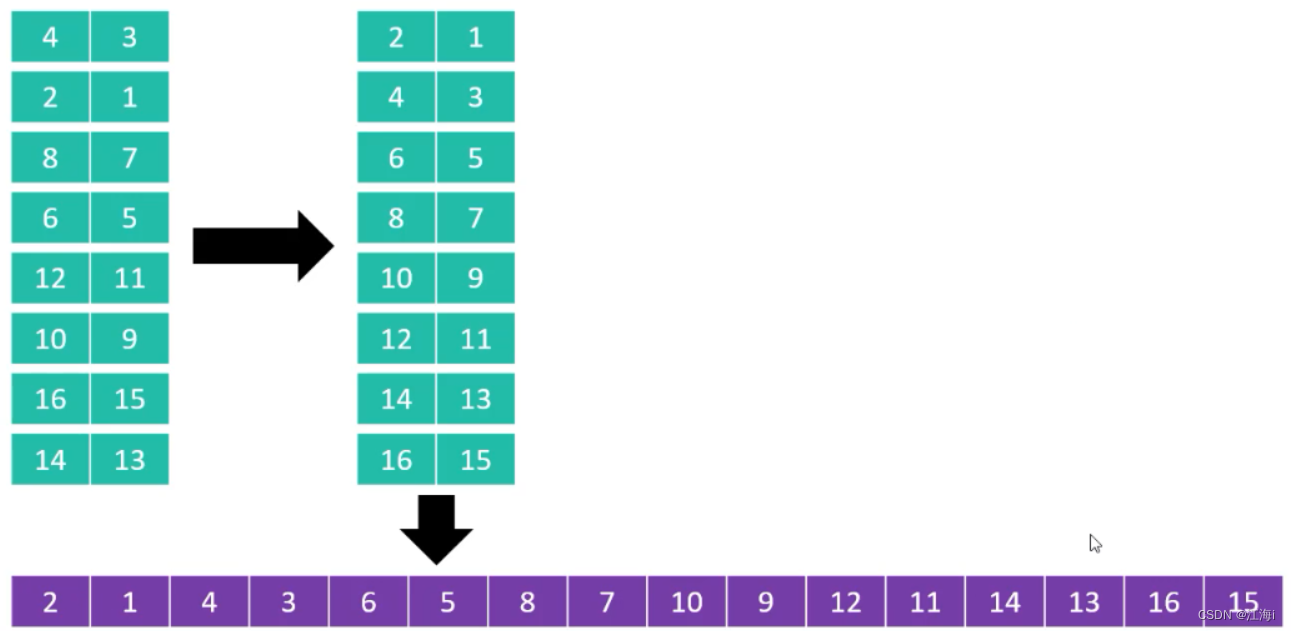
分成两列排序：
-
分成一列进行排序：
-
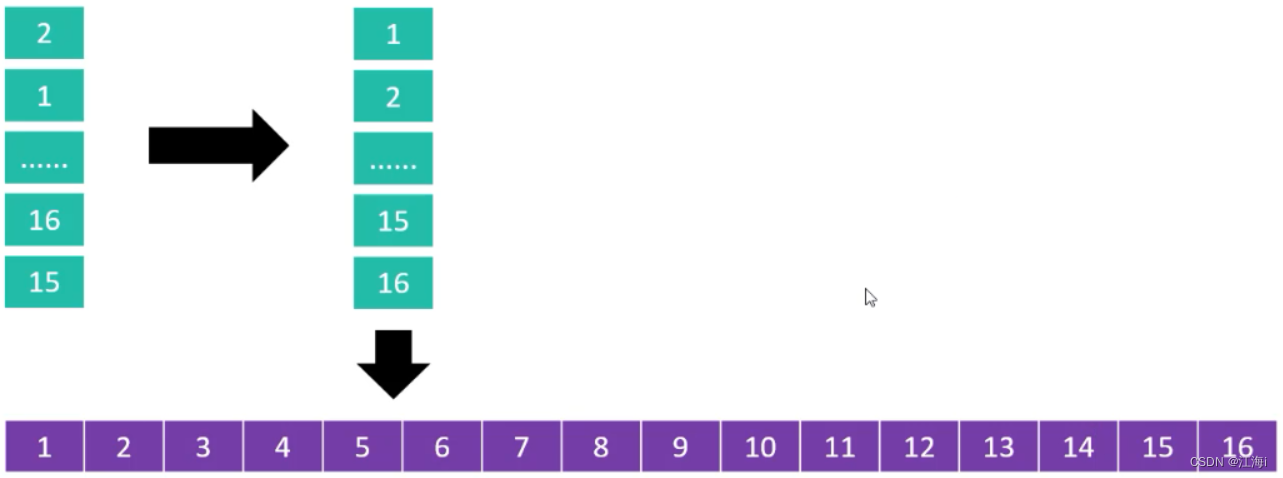
每排完一次，逆序对都在减少，因此希尔排序的底层使用插入排序来进行排序。
2.2 分析实现
这里的col为每次排序的列号，建议先看下小节完整代码再看这个分析。
- 插入排序代码：
for (int begin = 0; begin < arr.length; begin++) {
int cur = begin;
while (cur > 0 && cmp(cur, cur - 1) < 0){
swap(cur,cur - 1);
cur--;
}
}
-
因为使用希尔排序，并不是直接把
[begin,end)范围内所有的元素进行排序，而是将不同的列分别进行排序，且索引与行数、列数和步长的对应应该是列数 + 行数 * 步长，因此这里begin应该取列 + 步长，并且这里begin每次应该加step。例如：这里对第一列：11，6，1进行排序，他们在数组中的下标分别为0，5，10。且此时的步长为 5 。应该对索引0，5，10索引的值进行排序，而
begin每次应该加5.
-
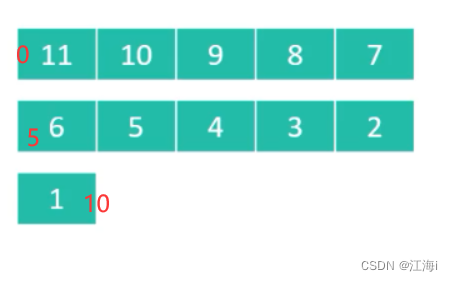
更改后的插入排序代码：
for (int begin = col + step; begin < arr.length; begin += step) {
int cur = begin;
while (cur > col && cmp(cur, cur - step) < 0){
swap(cur,cur - step);
cur -= step;
}
}
2.3 代码实现
/**
* @Description 希尔排序实现
* @date 2022/5/7 14:56
*/
public class ShellSort<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
// 步长序列
List<Integer> stepSequence = shellStepSequence();
for (Integer step : stepSequence) {
sort(step);
}
}
/**
* 分成step列进行排序
* @param step
*/
private void sort(int step){
for (int col = 0; col < step; col++) { // 循环对 列 进行排序
for (int begin = col + step; begin < arr.length; begin += step) {
int cur = begin;
while (cur > col && cmp(cur, cur - step) < 0){
swap(cur, cur - step);
cur -= step;
}
}
}
}
/**
* 希尔版本步长序列
* @return
*/
private List<Integer> shellStepSequence(){
List<Integer> stepSequence = new ArrayList<>();
int step = arr.length;
while ((step >>= 1) > 0){ // 每次将步长step除以二加入到步长序列中
stepSequence.add(step);
}
return stepSequence;
}
/**
* 最好版本步长序列
* @return
*/
private List<Integer> sedgewickStepSequence() {
List<Integer> stepSequence = new LinkedList<>();
int k = 0, step = 0;
while (true) {
if (k % 2 == 0) {
int pow = (int) Math.pow(2, k >> 1);
step = 1 + 9 * (pow * pow - pow);
} else {
int pow1 = (int) Math.pow(2, (k - 1) >> 1);
int pow2 = (int) Math.pow(2, (k + 1) >> 1);
step = 1 + 8 * pow1 * pow2 - 6 * pow2;
}
if (step >= arr.length) break;
stepSequence.add(0, step);
k++;
}
return stepSequence;
}
}
2.4 时间复杂度分析
希尔排序的时间复杂度取决于不同的步长序列。
- 希尔的步长序列：最坏时间复杂度为O(n2)。
/**
* 生成步长序列
* @return
*/
private List<Integer> shellStepSequence(){
List<Integer> stepSequence = new ArrayList<>();
int step = arr.length;
while ((step >>= 1) > 0){ // 每次将步长step除以二加入到步长序列中
stepSequence.add(step);
}
return stepSequence;
}
- 优化步长序列：最坏时间复杂度为O(n4/3)，1986年由Robert Sedgewick提出。
- 计算方法：
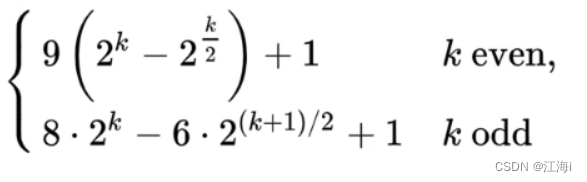
- 计算方法：
/**
* 最好版本步长序列
* @return
*/
private List<Integer> sedgewickStepSequence() {
List<Integer> stepSequence = new LinkedList<>();
int k = 0, step = 0;
while (true) {
if (k % 2 == 0) {
int pow = (int) Math.pow(2, k >> 1);
step = 1 + 9 * (pow * pow - pow);
} else {
int pow1 = (int) Math.pow(2, (k - 1) >> 1);
int pow2 = (int) Math.pow(2, (k + 1) >> 1);
step = 1 + 8 * pow1 * pow2 - 6 * pow2;
}
if (step >= arr.length) break;
stepSequence.add(0, step);
k++;
}
return stepSequence;
}
- 不是一个稳定排序算法
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
