正态分布及其应用

概率密度

概率密度等于一段区间(事件的取值范围)的概率除以该段区间的长度，它的值是非负的，可以很大也可以很小。概率密度不能是负值，概率密度可以大于1。

$$N(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-}\frac{(x-\mu {)}^2}{2{\sigma }^2}$$
e为自然对数的第2.718，

import numpy as np
import pandas as pd
from scipy import stats
# 绘图库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 设置浮点打印精度
%precision 3
# 显示图形
%matplotlib inline

x = 3
mu = 4
sigma = 0.8
# 方法一 列式计算
1/(np.sqrt(2*np.pi*sigma**2))*np.exp(-((x-mu)**2)/(2*sigma**2))
# 方法二 scipy.stats中的函数计算stats.norm.pdf
# loc为均值，scale为标准差
stats.norm.pdf(loc=4,scale=0.8,x=3)
# 绘制图形
x_plot = np.arange(start=1,stop=7.1,step=0.1)
plt.plot(x_plot,stats.norm.pdf(x=x_plot,loc=4,scale=0.8),color='black')

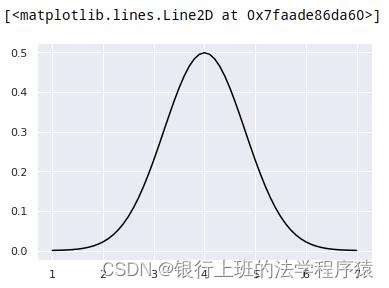
样本小于等于某值的比例

先从$N(x|4,0.8^2)$中抽样，样本容量为10万。

# 样本小于等于某值的比例
# 先从$N(x|4,0.8^2)$中抽样，样本容量为10万。
np.random.seed(1)
sim_sample = stats.norm.rvs(loc=4,scale=0.8,size=100000)
np.sum(sim_sample<=3)/len(sim_sample)

累积分布函数

$$F(X)=P(X\le x)$$
随机变量X，当x为实数时，F(X)为累积分布函数。计算随机变量小于等于某值的概率。
stats.norm.cdf(loc,scale,x)

# 累积分布函数
stats.norm.cdf(loc=4,scale=0.8,x=3)

无须计算数据个数，仅计算积分即可得到概率。是假设总体服从正态分布的优点。

左侧概率与百分位数

数据小于等于某个值的概率，借助累积分布函数可以得到左侧概率。
能得到某个概率的那个值就是百分位数，也叫左侧百分位数。

百分位数的实现

概率密度函数$N(x|\mu ,{\sigma }^2)$,$N(x|期望值均值，方差)$，

# 期望值为4，标准差0.8，求25%分位的分位数。
stats.norm.ppf(loc=4,scale=0.8,q=0.025)

左侧概率50%的 百分位数就是均值。

标准正态分布

均值为0，方差（或标准差）为1的正态分布$N(x|0,1^2)$。
统计量t值：
$$t=\frac{样本均值-总体均值}{标准误差}$$