CS224W 02-Properties of NetWorks, Random Graph Models 图网络特征，随机图模型

02-Properties of NetWorks, Random Graph Models

2.1 如何衡量一个网络

2.1.1 关键的网络的参数

Degree distribution:$P(k)$ （度分布）

Path length:$h$ （路径长度）

Clustering coefficient:$C$ (聚类系数)

Connected components:$s$ (连通分量)

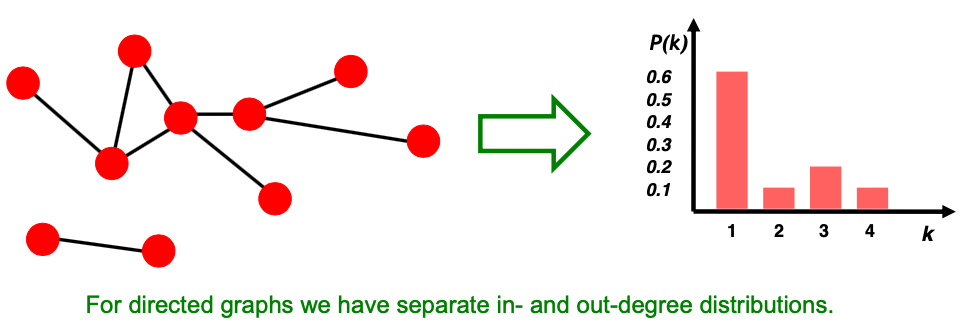
（1）Degree Distribution

Probability that a randomly chosen node has degree k

随机选择的节点的度为k的概率

Normalized histogram: 规范化的矩形图

$P(k)=N_k/N$

（2）Paths in a Graph

A path is a sequence of nodes in which each node is linked to the next one

A path can intersect（相交） itself and pass through the same edge multiple times

如：ACBDCDEG

距离（最短路径）：在一对节点中，通过最短路径经过的连接这些点的边。

如果两个节点没有被连接，那他们的距离经常被定义为无穷大或0

在有向图中，路径需要遵循箭头的方向。因此，距离就不是对称的了。B到C的距离不等于C到B的距离。

直径：在图的任意两个节点中的最大距离

平均路径长度：对于一个连通图或强连接有向图而言，

• 只计算连接的节点，不管路径长度为无限大或0的节点。
• 同样应用于一个图的连通分量。

（3）Clustering Coefficient（聚类系数）

对于无向图而言，聚类系数阐述的是节点i的邻居们的相互连接情况如何？

其中，节点i的度为 $k_i$