宽度优先搜索visit数组和入队之间的微妙关系

题目描述

有一个n*m的棋盘(1<n,m<=400)，在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步

输入输出格式

输入格式：

 

一行四个数据，棋盘的大小和马的坐标

 

输出格式：

 

一个n*m的矩阵，代表马到达某个点最少要走几步（左对齐，宽5格，不能到达则输出-1）

 

输入输出样例

输入样例#1： 复制

3 3 1 1

输出样例#1： 复制

0    3    2    
3    -1   1    
2    1    4    

分析：

本题如果在出队的时候才打标记，会导致超时，原因就是马的遍历是一种可能会重合的遍历

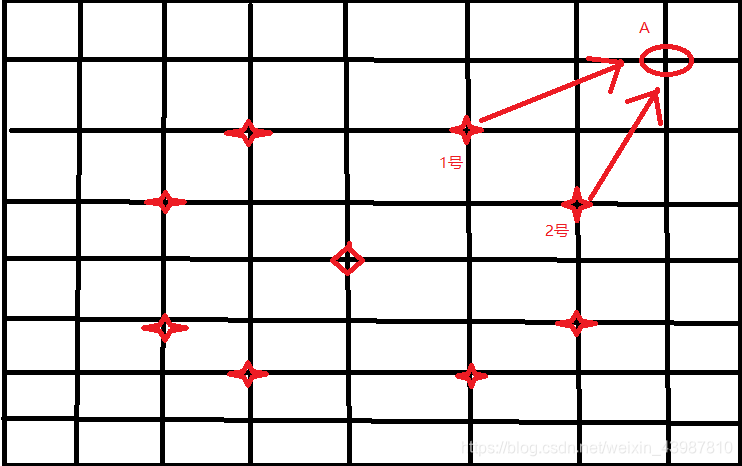
会出现A多次入队的情况，而A的每一次出队都要判断8次，因此超时。所以以后宽搜的时候一定要在入队之前打标记（如果标记是必要的话，其实本题根本不需要打标记，直接看步数数组即可）。

代码： 

#include <bits/stdc++.h>
using namespace std;
int n, m;
int x, y;
int step[410][410];
bool vis[410][410];
int dir[8][2] = {{-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}, {-2, -1}};
struct node
{
    int x, y;
    int step;
}temp, side;
void bfs()
{
    int i;

    queue<node> q;
    q.push((node){x, y, 0});
    step[x][y] = 0;
    vis[x][y] = true;
    while(!q.empty())
    {
        temp = q.front(), q.pop();
        for(i = 0; i < 8; i++)
        {
            side.x = temp.x + dir[i][0], side.y = temp.y + dir[i][1];
            int x = side.x, y = side.y;

            if(x > 0 && x <= n && y > 0 && y <= m && step[x][y] == -1)
            {
                vis[x][y] = true;
                step[x][y] = temp.step + 1;
                q.push((node){x, y, step[x][y]});
            }
        }
    }
    return;
}

int main()
{
    int i, j;

    memset(step, -1, sizeof(step));
    cin >> n >> m >> x >> y;

    bfs();
    for(i = 1; i <= n; i++)
    {
        for(j = 1; j <= m; j++)
            printf("%-5d", step[i][j]);
        printf("\n");
    }
    return 0;
}

ps:感谢付哥对本题tle的质疑，使我对宽搜进一步了解~