20.4.18 盛最多水的容器中等-优快云博客

探讨了一个经典的算法问题：如何在给定的垂直线中找到两条线，构成的容器能容纳最多的水。通过优化O(n²)解法，避免了超时问题，并详细解释了解题思路和代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构>成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。

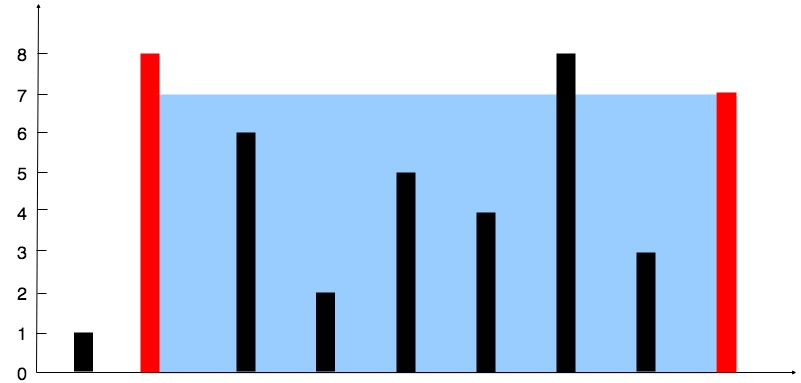
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水(表示为蓝色部分)的最大值为 49。

示例：
输入：[1,8,6,2,5,4,8,3,7]
输出：49

解题思路

一开始是大家都能想到的最暴力的O(n²)的解法，运行到最后几个用例就超时了；
现在修改过后也是O(n²)，但是没有超时了，简单的优化了一下；
从左往右循环遍历数组，找当前高度的最大容量。怎么找呢？这个高度的左边从左往右找比它高的，右边从右往左找比它高的，找不到的情况下，索引会和第一层循环的索引重合。然后不断更新最大容量；
只需要找第一个比它大的就行了，因为容量的高都是以矮的那一根作为高的。

代码思路

排除特殊情况；
变量result记录最大容量；
第二层循环，从左往右找比第一层循环中当前高度高的数，计算是否比最大容量大，是的话更新并跳出第二层循环；
当前高度右边的数和3同样的操作，改成从右往左。

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size()==0 || height.size()==1) return 0;

        int result=INT_MIN;
        for(int i=0; i<height.size(); i++){
            for(int left=0; left<i; left++){
                if(height[left]>=height[i]){
                    result=result<(i-left)*height[i]?(i-left)*height[i]:result;
                    break;
                }
            }
            for(int right=height.size()-1; right>i;right--){
                if(height[right]>=height[i]){
                    result=result<(right-i)*height[i]?(right-i)*height[i]:result;
                    break;
                }
            }
        }
        return result;
    }
};