RSA解密（不加解释推理）

RSA解密解题过程;
给出公私密钥(e,n)和(d,n)
首先要知道公密钥是公开的，会给你，密钥是不知道的，要你要求的
而会给出密文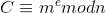
解密公式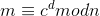
那问题就变成只要求出私钥怎么求，只要求出d，就可以利用快速幂来求得m
首先明确一点n一定是又两个质数相乘
难点就是要怎么把n分解成两个质数p,q。通常就是直接暴力
得到p,q有什么用呢
令f=(p-1)*(q-1)
则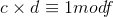
同样用扩展欧几里得算法可以求出d，进而求出m
所以对于这种题难点就是求出p和q,后面就是套模板了
如果担心两个数相乘会爆long long 有一个处理办法，先转成floor再转回longlong
实现函数：

ll fmul(ll a, ll b, ll mod) {
	ll d = (ll)floor(a * (long double)b / mod + 0.5);
	ll ret = (a * b - d * mod) % mod;
	if (ret < 0) {
		ret += mod;
	}
	return ret;
}在这里插入代码片

用扩展欧几里得求cd%n=1，求得d，该等式可以变成cd-kn=1,其中k=(cd)/n;则相当于ax+by=1
中的x。