线段树算法的一道较难的题：球星----记忆化归并排序（线段树）+二分

最新推荐文章于 2021-09-18 09:59:52 发布

偶耶XJX

最新推荐文章于 2021-09-18 09:59:52 发布

阅读量341

点赞数 1

CC 4.0 BY-SA版权

分类专栏：信息竞赛解题

本文链接：https://blog.youkuaiyun.com/weixin_43960287/article/details/86547537

信息竞赛解题专栏收录该内容

194 篇文章

订阅专栏

本文深入解析了一道关于查询特定时间段内能力值最高的前11名球员的问题，采用离散化和线段树进行优化，避免了传统方法的超时问题。通过将球员年份排序和离散化，利用线段树存储和合并区间内的球员信息，大幅提升了查询效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

球星

时间限制: 10 Sec 内存限制: 128 MB

题目描述

给出球星们的能力值、年份、名字，有很多个查询，每个查询给出一个年份的范围，求出这个范围里能力值从高到低排列的前11名球员，如果能力值相同则按年份从低到高排，如果年份仍然相同，则按名字的字典序排。如果不足11个球员，就用XXX代替输出凑够11行。

输入

输入数据：
第一行包含1个整数N（1<=N<=50000）,表示球星的总数，接下来N行，每行描述了1个球星（year,name,ability）。0<=year<=1000000000,name不超过15个字母，0<=ability<=1000000000.
假设没有两个人的名字相同。接下来有一个整数R，表示有R个查询。接下来R行，每行描述了一个产寻，每个查询包含2个整数（x,y）,表示从第x年到第y年。（0<=x<=y<=1000000000）

输出

输出数据：对于每组数据，按上面描述的顺序输出最靠前的11个球员的名字，每个球员占一行。如果不足11行，则用XXX代替，凑够11行。每组数据后都有一个空行。

样例输入

样例输出

c
b
a
XXX
XXX
XXX
XXX
XXX
XXX
XXX
XXX

d
e
XXX
XXX
XXX
XXX
XXX
XXX
XXX
XXX
XXX

解题方法推导

这道题其实很好理解：就是求给定时间段内能力值靠前的11名球星的名字（不足11名的“XXX”补足）。

于是我~~极其不负责任地~~打了爆搜：所有球星排序一遍，每次把符合的球星输出（如下）。

#include<string>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
LL n,i,j,k,p,a,b;
struct itn{
    LL y,nl;
    char na[20];
}x[50005];
inline LL read(){
    LL x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
bool cmp(itn a,itn b){
    if(a.nl!=b.nl)return a.nl>b.nl;
    else if(a.y!=b.y)return a.y<b.y;
    else return strcmp(b.na,a.na)>0;
}
int main()
{
    n=read();
    for(i=1;i<=n;i++){
        x[i].y=read();
        scanf("%s",x[i].na);
        x[i].nl=read();
    }
    sort(x+1,x+1+n,cmp);
    p=read();
    while(p--){
        a=read(),b=read();
        for(i=1,j=1;i<=n&&j<=11;i++){
            if(x[i].y>=a&&x[i].y<=b){
                puts(x[i].na);j++;
            }
        }
        for(;j<=11;j++){
            puts("XXX");
        }
        putchar('\n');
    }
    return 0;
}

于是我惨烈地超时了。

由此可知，虽然询问数R没划定限制，但最高一定在100000以上（不然怎么会超时嘞）。

所以，我们要改进方法：

当前的每次输出都要遍历一遍查找球星，如何让这个时间缩短？

当然是尽可能地直接用存好的球星名单噻。（空间换时间）

1.如果每个时间段都存下其对应的球星们，那么要开 a[ 1000000000000000000 ] 的数组，肯定超空间。（不行）

2.如果把球星的年份升序排序，把排完后的数组下标作为“时间点”构成区间，这样每个“时间点”都存了球星信息且不浪费（离散化），(同样把这里的每个“时间段”都存下对应的球星)虽然空间少了很多，但也要开 a[ 2500000000 ] 的数组，空间也超了。（不行）

于是我想到各种存法并一一比较，最后发现以二叉线段树存储既省空间又省时~~（其实是直接想到的）~~。

（离散化基础上）每个节点储存一个有序的球星名单，只用 a[200000] 空间。

而由于归并排序就是利用二分递归排的序，所以我们可以：每次遍历节点时，把它的子节点存的有序序列合并，并存在当前节点。

这样就建好树了。

每次把询问的两个时间点通过两个不同的二分搜索确定在球星年份升序序列中的两个下标（构成一个区间），再插入线段树中找出可以组成它的所有区间，最后把它们存的序列合并起来，就是所要找的球星名单啦！

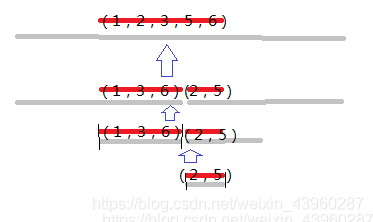
（为什么要用两个不同的二分呢？比如年份1～3的球星有6位，年份分别为1，1，1，3，3，3，用同种二分要么是第一个到第四个，要么是第三个到第六个，只有用一个二分专搜前端，一个专搜后端，才可以一个球星不漏地搜出来。）

详细理解请看代码。

代码

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
LL n,i,j,k,p,a,b;
struct itn{
    LL y,nl;
    char na[20];
}x[50005];
vector<int>G[200005],f;
int c[15],len;
int h[50005];
inline LL read(){
    LL x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
bool cmp(itn a,itn b){
    if(a.nl!=b.nl)return a.nl>b.nl;
    else if(a.y!=b.y)return a.y<b.y;
    else return strcmp(b.na,a.na)>0;
}
bool cmp2(itn a,itn b){
    return a.y<b.y;
}
void AC(int l,int r,int i){
    int mid=(l+r)/2;
    if(l==r){
        G[i].clear();
        G[i].push_back(l);
        return;
    }
    AC(l,mid,i*2);
    AC(mid+1,r,i*2+1);
    int a=0,b=0;
    G[i].clear();
    while(G[i].size()<11&&a<G[i*2].size()&&b<G[i*2+1].size()){
        if(cmp(x[G[i*2+1][b]],x[G[i*2][a]])){
            G[i].push_back(G[i*2+1][b]);
            b++;
        }
        else G[i].push_back(G[i*2][a]),a++;
    }
    while(G[i].size()<11&&a<G[i*2].size())G[i].push_back(G[i*2][a]),a++;
    while(G[i].size()<11&&b<G[i*2+1].size())G[i].push_back(G[i*2+1][b]),b++;
}
void guib(int l,int r,int i,int a,int b){
    int mid=(l+r)/2;
    if(l==a&&r==b){
        int p=0,q=0;
        f.clear();
        while(f.size()<11&&p<len&&q<G[i].size()){
            if(cmp(x[G[i][q]],x[c[p]])){
                f.push_back(G[i][q]);
                q++;
            }
            else f.push_back(c[p]),p++;
        }
        while(f.size()<11&&p<len)f.push_back(c[p]),p++;
        while(f.size()<11&&q<G[i].size())f.push_back(G[i][q]),q++;
        for(len=0;len<f.size();len++)c[len]=f[len];
        return;
    }
    if(a<=mid)guib(l,mid,i*2,a,min(mid,b));
    if(b>mid)guib(mid+1,r,i*2+1,max(a,mid+1),b);
}
inline int id1(int s){
    int l=1,r=n,mid=(l+r)/2;
    while(l<r){
        if(s>x[mid].y)l=mid+1;
        else r=mid;
        mid=(l+r)/2;
    }
    return mid;
}
inline int id2(int s){
    int l=1,r=n,mid=(l+r+1)/2;
    while(l<r){
        if(s<x[mid].y)r=mid-1;
        else l=mid;
        mid=(l+r+1)/2;
    }
    return mid;
}
int main()
{
    n=read();
    for(i=1;i<=n;i++){
        x[i].y=read();
        scanf("%s",x[i].na);
        x[i].nl=read();
    }
    sort(x+1,x+1+n,cmp2);
    AC(1,n,1);
    p=read();
    while(p--){
        a=read(),b=read();
        len=0;
        guib(1,n,1,id1(a),id2(b));
        for(i=0;i<len;i++)
            puts(x[c[i]].na);
        for(;i<11;i++)puts("XXX");
        putchar('\n');
    }
    return 0;
}

尾语

欢迎关注我的博客偶耶(xiong j x)