动态规划一-优快云博客

本文通过杨辉三角的两种实现方式介绍动态规划的入门应用，详细解释了每一步的逻辑，并展示了如何从零基础理解算法。同时，文章还探讨了爬楼梯问题，揭示了其与杨辉三角类似的动态规划解法，以及如何通过滚动数组优化空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言：

本专栏只专注动态规划的解法，若有其它简便解法暂不考虑。
从几乎零基础开始学算法，多多包涵，共同进步！

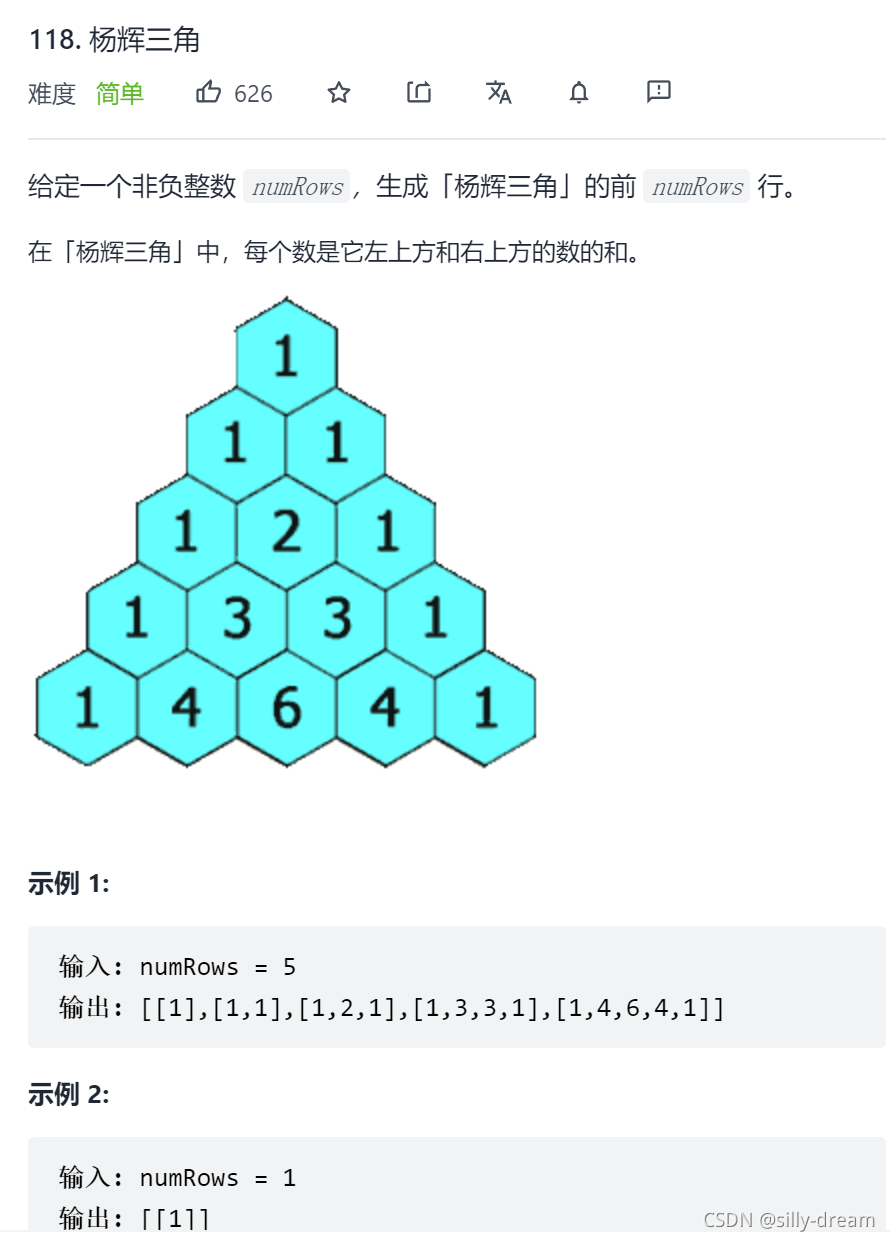
杨辉三角一

杨辉三角是不需要了解动态规划，就能用动态规划解法做出来的动态规划的入门典例，因为你有意无意就能用动态规划的解法来解题。
在这里插入图片描述

在这里插入图片描述

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();

        for (int i = 0; i < numRows; i++){//行
            List<Integer> row = new ArrayList<Integer>();
            for(int j = 0;j<= i;j++){//列
                if (j==0 || j==i){
                    row.add(1);
                }else{
                    row.add(ans.get(i-1).get(j-1)+ans.get(i-1).get(j));
                }              
            }
            ans.add(row);
        }
        return ans;
    }
}

思路：按题意就指明了每个数是左上方和右上方的数的和。
直接两层循环解决。
注意：每行的第一个数和最后一个数都是1；
返回类型为List<List>，要了解一定的List集合知识

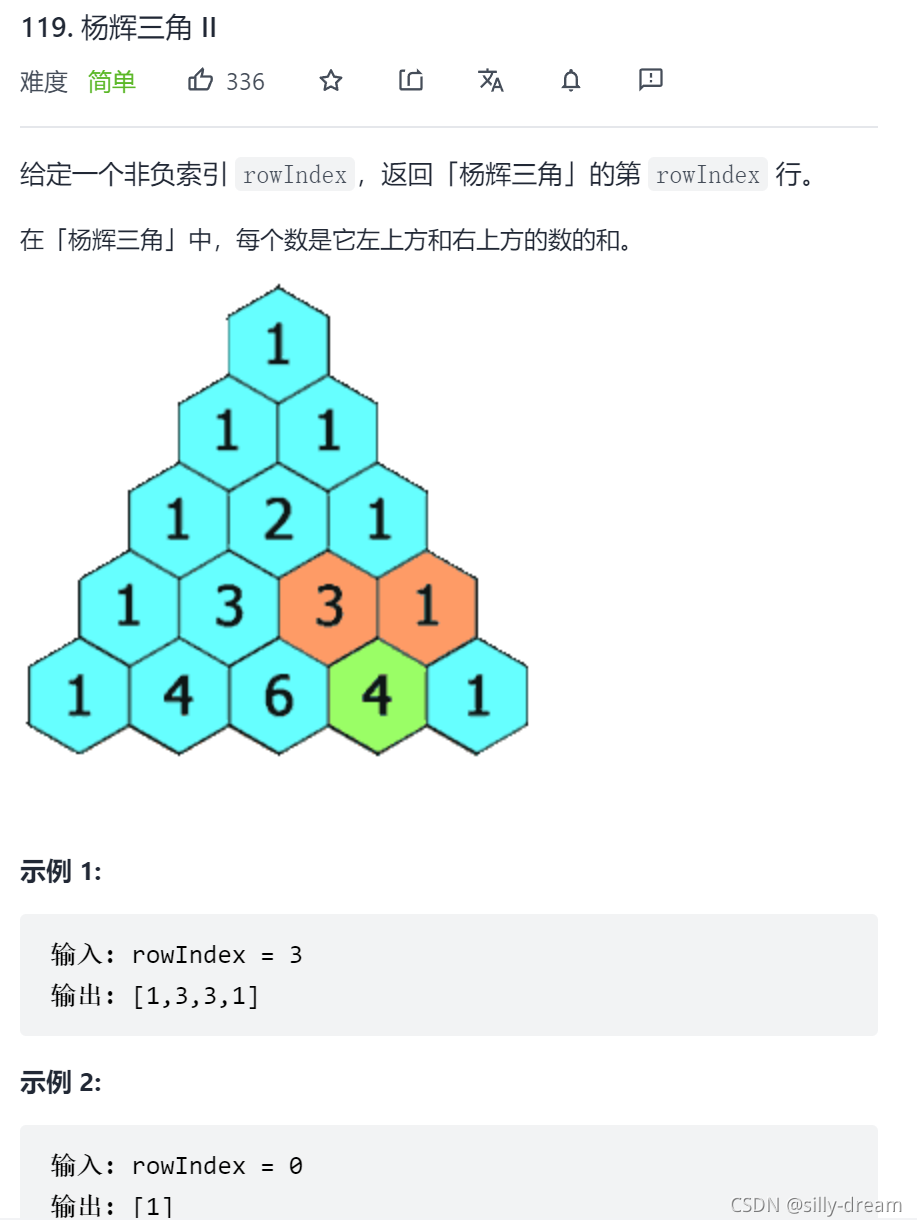
杨辉三角二

在这里插入图片描述

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();

        for (int i = 0; i <= rowIndex; i++){//行
            List<Integer> row = new ArrayList<Integer>();
            for(int j = 0;j<= i;j++){//列
                if (j==0 || j==i){
                    row.add(1);
                }else{
                    row.add(ans.get(i-1).get(j-1)+ans.get(i-1).get(j));
                }  
                if(i==rowIndex&&j==rowIndex) return row;            
            }
            ans.add(row);
            
        }
        return null;
    }
}

在这里插入图片描述

思路：跟上一题大同小异，差别就是返回类型为List，所以直接拷
贝，再稍加修改，在内层循环里面加上一个判断
if(irowIndex&&jrowIndex) return row;

爬楼梯

在这里插入图片描述

class Solution {
    public int climbStairs(int n) {
      int q = 0,p = 1,t=0;
      for(int i = 0;i<n;i++){
          t = q;
          q = p;
          p = t + p;    
      }
       return p;
    }
}