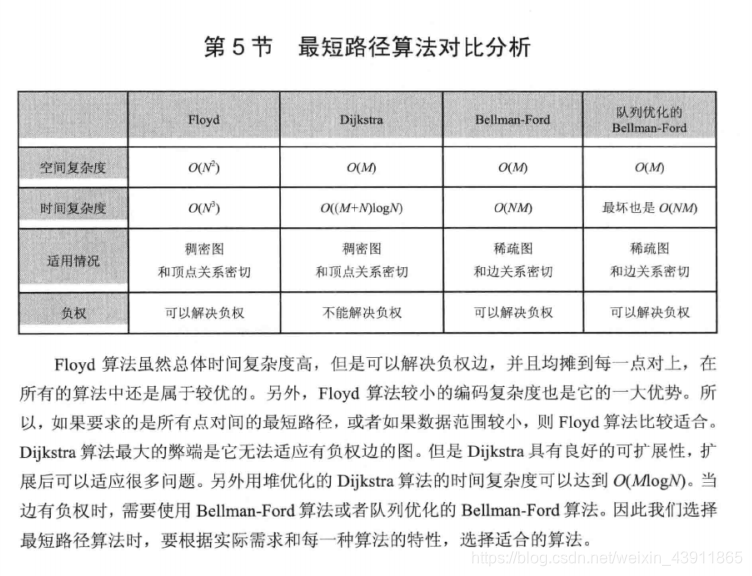
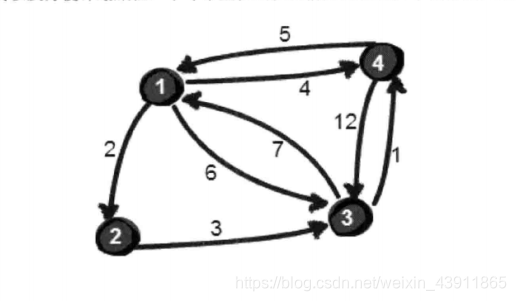
/*Floyd算法求最短路径,图中不能带有“负权回路” */
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (Map[i][j] > Map[i][k] + Map[k][j])
Map[i][j] = Map[i][k] + Map[k][j];
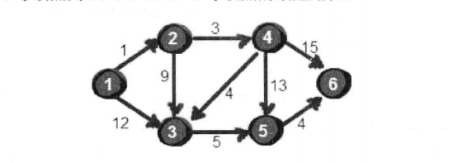
/*Dijkstra算法求最短路径*/
#define inf 99999999
for (int i = 1; i <= n - 1; i++)//n个顶点
{
//找到离1号顶点最近的点
min = inf;//inf是无穷大
for (int j = 1; j <= n; j++)
{
if (book[j] == 0 && dis[j] < min)
{
min = dis[j];
u = j;
}
}
book[u] = 1;
//遍历每一个点
for (int v = 1; v <= n; v++)
{
if (Map[u][v] < inf)
{
if (dis[v] > dis[u] + Map[u][v])
dis[v] = dis[u] + Map[u][v];
}
}
}
/*Bellman-Ford算法求最短路径*/
#define inf 99999999
for (int k = 1; k <= n - 1; k++)
{
//备份dis数组,优化
for (int i = 1; i <= n; i++)
bak[i] = dis[i];
//进行一轮松弛
for (int i = 1; i <= m; i++)
if (dis[v[i]] > dis[u[i]] + w[i])
dis[v[i]] = dis[u[i]] + w[i];
//检测dis数组是否有更新
check = 0;
for(int i=1;i<=n;i++)
if (bak[i] != dis[i])
{
check = 1;
break;
}
if (check == 0)//若没有更新,则提前退出循环
break;
}





















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








