HDU-6608 Fansblog【2019 Multi-University Training Contest 3】【威尔逊定理】【逆元】

本文链接：https://blog.youkuaiyun.com/weixin_43895356/article/details/98208397

本文探讨了在给定范围内寻找素数及其前一个素数的因子，并利用威尔逊定理解决特定数学问题的方法。通过快速乘法和逆元求解技巧，文章提供了一种高效的算法实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Fansblog

Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1978 Accepted Submission(s): 808

Problem Description

Farmer John keeps a website called ‘FansBlog’ .Everyday , there are many people visited this blog.One day, he find the visits has reached P , which is a prime number.He thinks it is a interesting fact.And he remembers that the visits had reached another prime number.He try to find out the largest prime number Q ( Q < P ) ,and get the answer of Q! Module P.But he is too busy to find out the answer. So he ask you for help. ( Q! is the product of all positive integers less than or equal to n: n! = n * (n-1) * (n-2) * (n-3) *… * 3 * 2 * 1 . For example, 4! = 4 * 3 * 2 * 1 = 24 )

Input

First line contains an number T(1<=T<=10) indicating the number of testcases.
Then T line follows, each contains a positive prime number P (1e9≤p≤1e14)

Output

For each testcase, output an integer representing the factorial of Q modulo P.

Sample Input

1
1000000007

Sample Output
328400734

Source

HDU-6608

题意

T组样例，每组样例给出一个1e9到1e14范围的素数P，Q小于P，Q是P前一个素数。求Q!%P。

思路

威尔逊定理：判定一个自然数是否为素数的充分必要条件。即：当且仅当p为素数时：( p -1 )! ≡ -1 ( mod p )；
由威尔逊定理可以得到

( P - 1 )! % ( P ) == -1 % P，即( P - 1 )! % P == P - 1
( P - 1 )! == Q ! * ( Q + 1 ) * ( Q + 2 ) * ... * ( P - 1)

所以
Q! % P ==
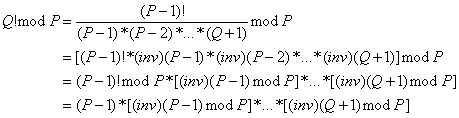
所以只需要求( P - 1 ) 乘 [ Q + 1, P - 1 ] 逆元就可以了，
两个素数之间最多相隔246个数，所以直接for循环向下判断，暴力判断素数就行，另外因为数太大所以乘法的地方用快速乘

快速乘

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
ll mul(ll x,ll y,ll p) {
	ll z = (ld)x / p * y;
	ll res=(ull)x * y - (ull)z * p;
	return (res + p) % p;
}

求逆元

ll qkpow(ll a,ll p,ll mod) {
	ll t = 1,tt = a % mod;
	while(p) {
		if (p & 1) t = mul(t, tt, mod);
		tt = mul(tt, tt, mod);
		p >>=  1;
	}
	return t;
}

ll getInv(ll a,ll mod) {
	return qkpow(a,mod-2,mod);
}

代码

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
ll P;

bool is_prime(ll x) {
	for(ll i = 2; i * i <= x; i++) {
		if(x % i == 0) return false;
	}
	return true;
}

ll mul(ll x,ll y,ll p) {
	ll z=(ld)x/p*y;
	ll res=(ull)x*y-(ull)z*p;
	return (res+p)%p;
}

ll qkpow(ll a,ll p,ll mod) {
	ll t = 1,tt = a % mod;
	while(p) {
		if (p & 1) t = mul(t, tt, mod);
		tt = mul(tt, tt, mod);
		p >>=  1;
	}
	return t;
}

ll getInv(ll a,ll mod) {
	return qkpow(a,mod-2,mod);
}

int main() {
	int t;
	while(~scanf("%d", &t)) {
		while(t--) {
			scanf("%lld", &P);
			ll Q = P - 1;
			ll res = P - 1;
			while(!is_prime(Q)) {
				res = mul(res, getInv(Q, P), P);
				Q--;
			}
			printf("%lld\n", res);
		}
	}
}