WUSTOJ 1891 低价购买【DP】-优快云博客

博客围绕低价购买问题展开，利用动态规划（DP）和最长递增子序列（LIS）求解。通过三个数组f、dp、sum，先进行DP找出各点最大购买次数，再搜索剔除重复方案数并递推总方案数，还对sum数组赋值做了特殊处理以方便递推。

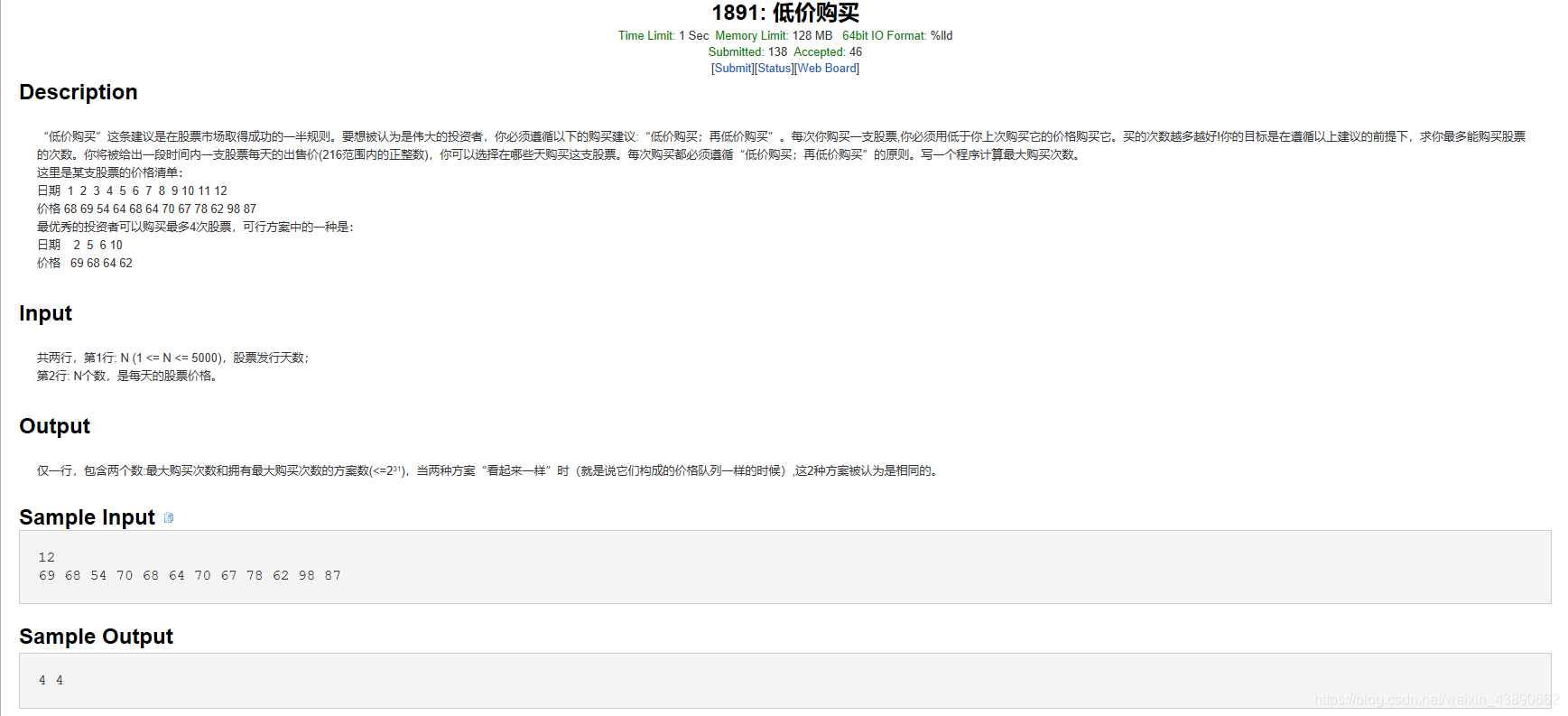
题目来源：http://acm.wust.edu.cn/problem.php?id=1891&soj=0
在这里插入图片描述
★不知道开始怎么写的，现在都不会了，~~菜鸡如我~~ ，最后决定发一篇博客（~~可能会凑一个DP专栏233~~ ）

思路：

三个数组，f存输入的数据，dp就是用来DP的，dp[ i ]表示第i个点最大购买次数，sum该点的存方案数
然后首先DP找出每个点的最大购买次数，这个过程是叫LIS，~~看好些博客都是这么叫的~~
然后再搜索一次，
如果dp[i]==dp[j]&&f[i]==f[j] 去掉重复了的相同方案数
例如 3 2 1 3 2 1 的情况,dp[3]=dp[6] f[3]=f[6],这个时候方案数相同，肯定要剔除
如果 if(dp[i]==dp[j]+1&&f[i]<f[j]) 递推总方案数 6 4 2 3 1 这时dp[5]=dp[3]+1, 2<4 ,sum[5]+=sum[3]
注意：
最后sum[i]=0变1 ，不然最后递推的都是0。很多人可能想知道为什么不一开始让sum[i]=1呢？其实，这是为了递推出关系，如果一开始都赋值为1了，那上面那个例子 6 4 2 3 1 最后结果是sum[5]+=1; sum[5]=2;但是这个地方应该是sum[5]=1；只让那些没有被递推的等于1，方便后面再递推而已

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=5050;
int f[maxn],dp[maxn],sum[maxn];
int main()
{
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++) scanf("%d",f+i);
        memset(dp,0,sizeof dp);
        memset(sum,0,sizeof sum);
        int mm=0;
        for(int i=1;i<=n;i++){
            int m=0;
            for(int j=1;j<i;j++)
                if(f[i]<f[j]) m=max(m,dp[j]);
            dp[i]=m+1;
            mm=max(dp[i],mm);
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<i;j++){
                if(dp[i]==dp[j]&&f[i]==f[j]) sum[j]=0;
                if(dp[i]==dp[j]+1&&f[i]<f[j]) sum[i]+=sum[j];
            }
            if(sum[i]==0) sum[i]=1;
        }
        int ans=0;
        for(int i=1;i<=n;i++)
            if(dp[i]==mm) ans+=sum[i];
        cout<<mm<<' '<<ans<<endl;
    }
    return 0;
}