图像的变换——fft/ ifft、fftn、fft2、dct2、dict2、dctmtx

一、离散傅立叶变换

1.fft/ ifft——快速傅立叶变换/反变换

• Y=fft(X)/Y=ifft(X)函数
  按照基2的算法对X进行快速傅立叶变换/反变换。若X是一个矩阵，则对矩阵的每列进行快速傅立叶变换l反变换，返回Y是和X相同大小的矩阵。若X是一个多维序列，则对第一个非单独维进行快速傅立叶变换/反变换。
• Y=fft(X,n)/Y=ifft(×,n)函数
  对X进行n点快速傅立叶变换/反变换。当X是一个向量，若X的长度小于n，则先对X进行补零使其长度为n;若X的长度大于n，则对X进行剪切使其长度为n，最后得到一个长度为n的向量Y。当X是一个矩阵，则利用同样方法对矩阵的每一列进行调整，然后对矩阵的每列进行快速傅立叶变换/反变换，最后得到一个n行的矩阵Y。
• Y=fft(X,n,dim)/Y=ifft(×,n,dim)
  用法同上。dim用来指定进行快速离散傅立叶变换/反变换的维数。

2.fftn-进行n维快速傅里叶变换

• Y = fftn(X)运用多维快速傅里叶变换（FFT)算法，计算X的n维离散傅里叶变换值。参量X可为向量、矩阵和多维数组。
• Y = fftn(X,size)运用多维快速傅里叶变换(FFT）算法，计算X的n维离散傅里叶变换值。参量size为向量，其元素指定变换前X各维的大小。如果X的维数与size不同，则对X进行补零或截短后进行计算。

代码示例：

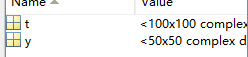
y = fftn(rand(50));
t = fftn(rand(50),[100 100]);

运行结果：

3.fft2-进行2维快速傅里叶变换

• Y =fft2(X)计算矩阵X的二维离散傅里叶变换矩阵Y。X和Y的维数相同。
• Y = fft2(×,m,n)计算矩阵X的二维离散傅里叶变换矩阵Y。在变换前先将X补零至m×n矩阵。如果m或n比A的维数小，则将X截短。Y的维数为m×n。

代码示例：