A/B 可以用拓展欧几里得或者欧拉定理做

原创于 2019-07-11 10:55:11 发布 · 218 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数论

数论同时被 3 个专栏收录

12 篇文章

订阅专栏

欧拉定理

4 篇文章

订阅专栏

拓展欧几里得

2 篇文章

订阅专栏

博客介绍了利用拓展欧几里得和欧拉定理求逆元的方法。通过拓展欧几里得可得到b和9973的一组解，其中x为b的逆元，题目中的A%9973乘以逆元可得答案。欧拉定理方面，因gcd(B,9973) = 1，可推出b的9971次方相关结果用于求逆元。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

A/B
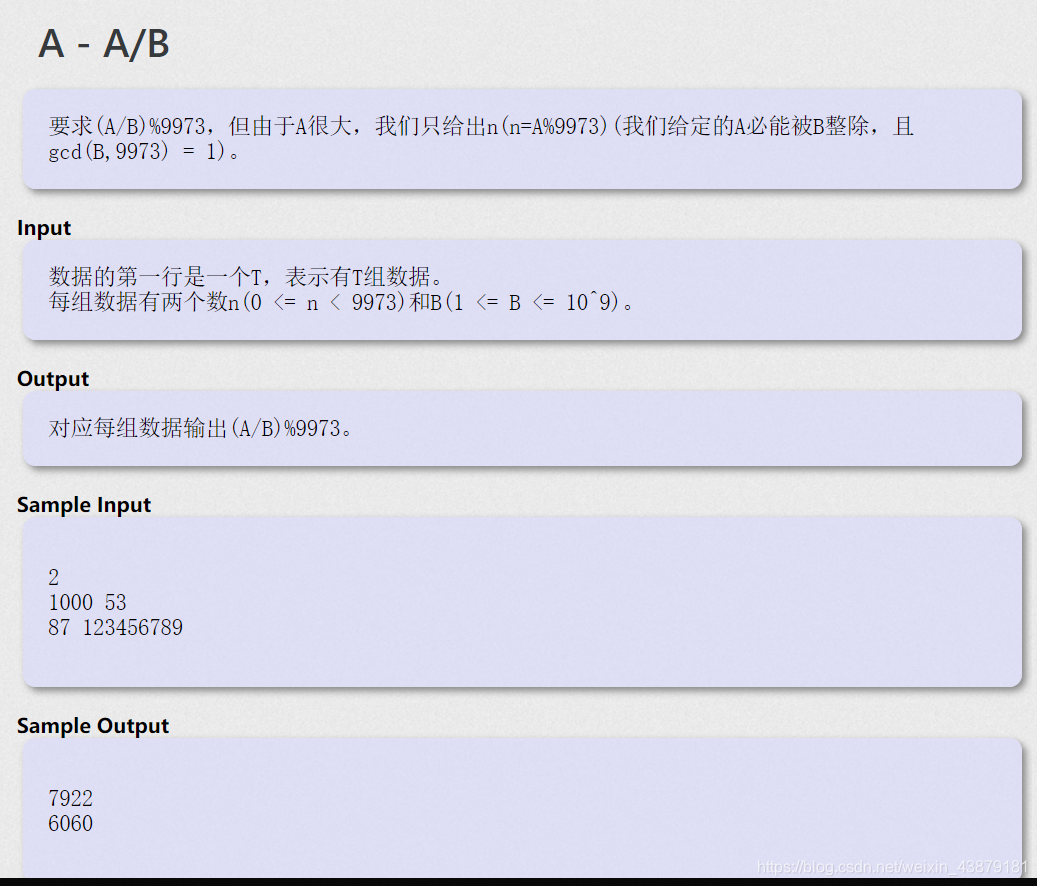
拓展欧几里得
b和9973的一组解，x就是b的逆元，所以题目给的A%9973直接*逆元就得到答案
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a,ll b,ll &x,ll &y) {
	if(!b) {
		x=1;
		y=0;
		return a;
	}
	ll d=exgcd(b,a%b,x,y);
	ll t=x;
	x=y;
	y=t-a/b*y;
	return d;
}
int main() {
	ll t,n,b,x,y;
	cin>>t;
	while(t--) {
		cin>>n>>b;
		exgcd(b,9973,x,y);
		cout<<((x*n)%9973+9973)%9973<<'\n';//保证是不超过模的最大正数
	}
	return 0;
}

欧拉定理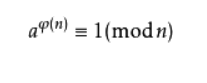在这里插入图片描述
因为gcd(B,9973) = 1)，显然b的9972次方次取余9973是1，方程两边同时*1/b，左边是b的9971，右边是1/b

因为求1/b，因为取模不影响乘法影响除法，所以用1/b和a乘就好了，现在只需要求b的9971次方
在这里插入图片描述

#include <iostream>
#include <algorithm>
using namespace std;
const int mod=9973;
int main()
{
    long long int a,b;
    int t;
    cin>>t;
    while(t--){
        cin>>a>>b;
        int n=9971;
        long long ans=1;
        while(n){//快速幂
            if(n&1)
                ans=(ans*b)%mod;
            b=(b*b)%mod;
            n>>=1;
        }
        ans=(a%mod)*(ans%mod)%mod;
        cout<<ans<<endl;
    }
    return 0;
}