文章目录
一、定义
1. KL距离(Kullback–Leibler divergence)
设P, Q为两个概率(意思就是sum为1,相当于做完softmax之后的效果),则KL距离 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)被定义为
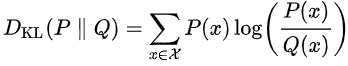
2. torch.nn.KLDivLoss()
一个类(class),通过调用(__call__)来实现loss的计算。官网的定义如下:
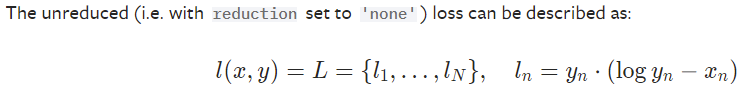
这里可以看出来,y相当于P,x相当于Q。想要实现KL距离 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)的话,其使用方法为
# P, Q are two probabilities (normally after softmax)
l = torch.nn.KLDivLoss()
loss = l(torch.log(Q), P)
这是很显然的,因为根据官网定义
l n = y n ⋅ ( log y n − x n ) = y n ⋅ ( log y n − log Q n ) = P n ⋅ ( log P n − log Q n ) = P n ⋅ log P n Q n \begin{aligned} l_n &= y_n \cdot (\log y_n - x_n)\\ &= y_n \cdot (\log y_n - \log Q_n) \\ & = P_n\cdot (\log P_n - \log Q_n) \\ & = P_n\cdot \log \frac{P_n}{ Q_n} \end{aligned} ln=yn





 本文详细介绍了KL距离的概念,以及在PyTorch中如何使用`torch.nn.KLDivLoss()`和`torch.nn.functional.kl_div()`计算损失。通过实验对比,展示了这两个函数在实际应用中的计算一致性,并提供了在深度学习模型中应用KL距离的伪代码示例。
本文详细介绍了KL距离的概念,以及在PyTorch中如何使用`torch.nn.KLDivLoss()`和`torch.nn.functional.kl_div()`计算损失。通过实验对比,展示了这两个函数在实际应用中的计算一致性,并提供了在深度学习模型中应用KL距离的伪代码示例。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








