*python3__leecode/0094. 二叉树的中序遍历

一、刷题内容

原题链接

https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

内容描述

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1：

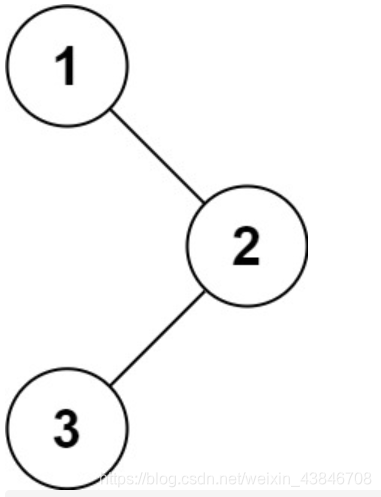
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[2,1]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

二、解题方法

1.方法一：递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def inorder(root):
            if not root:
                return
            inorder(root.left)
            res.append(root.val)
            inorder(root.right)
        inorder(root)
        return res

2.方法二：迭代

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        if not root:
            return res
        stack = []
        node = root
        while stack or node:
            while node:
                stack.append(node)
                node = node.left
            node = stack.pop()
            res.append(node.val)
            node = node.right
        return res

3.方法三：简递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        return self.inorderTraversal(root.left)+[root.val]+self.inorderTraversal(root.right)

4.方法四：Morris中序遍历

Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：

1、如果 x 无左孩子，先将 x 的值加入答案数组，再访问 x 的右孩子，即 x=x.right。
2、如果 x 有左孩子，则找到 x 左子树上最右的节点（即左子树中序遍历的最后一个节点，x 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。

如果 predecessor 的右孩子为空，则将其右孩子指向 x，然后访问 x 的左孩子，即 x=x.left。

如果 predecessor 的右孩子不为空，则此时其右孩子指向 x，说明我们已经遍历完 x 的左子树，我们将 predecessor 的右孩子置空，将 x 的值加入答案数组，然后访问 x 的右孩子，即x=x.right。

3、重复上述操作，直至访问完整棵树。

其实整个过程我们就多做一步：假设当前遍历到的节点为 x，将 x 的左子树中最右边的节点的右孩子指向 x，这样在左子树遍历完成后我们通过这个指向走回了 x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

class Solution(object):
	def inorderTraversal(self, root):
		res = []
		pre = None
		while root:
			# 如果左节点不为空，就将当前节点连带右子树全部挂到
			# 左节点的最右子树下面
			if root.left:
				pre = root.left
				while pre.right:
					pre = pre.right
				pre.right = root
				# 将root指向root的left
				tmp = root
				root = root.left
				tmp.left = None
			# 左子树为空，则打印这个节点，并向右边遍历	
			else:
				res.append(root.val)
				root = root.right
		return res

5.方法五：颜色标记法

其核心思想如下：

使用颜色标记节点的状态，新节点为白色，已访问的节点为灰色。
如果遇到的节点为白色，则将其标记为灰色，然后将其右子节点、自身、左子节点依次入栈。
如果遇到的节点为灰色，则将节点的值输出。

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        WHITE, GRAY = 0, 1
        res = []
        stack = [(WHITE, root)]
        while stack:
            color, node = stack.pop()
            if node is None: continue
            if color == WHITE:
                stack.append((WHITE, node.right))
                stack.append((GRAY, node))
                stack.append((WHITE, node.left))
            else:
                res.append(node.val)
        return res