4月10号dp专项补题（D题学完状压DP后再补）

A - Clique in the Divisibility Graph （*1600）

——题意——
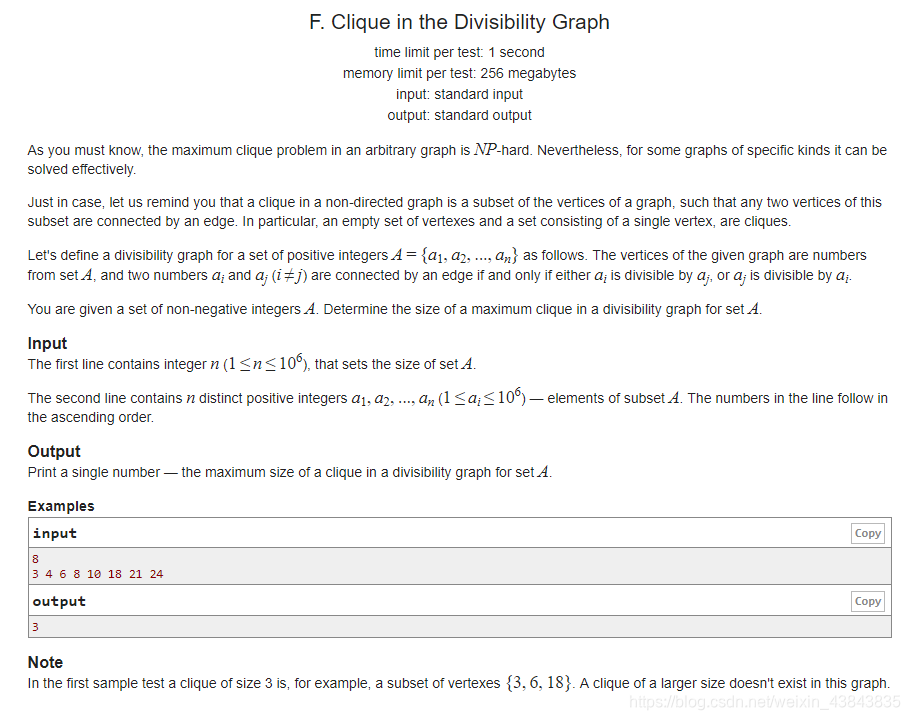
给出一个长度为n的数字集合{an}（给出时已满足单调增），要求从中找出一个最长的子序列，该子序列满足后一个数字正好对前一个数字取模为0，输出这个子序列的长度。样例中的序列为3、6、18或4、8、24.
其中，序列长度1<=n<=1e6，序列中元素大小1<=ai<=1e6.

——题解——
这题我是看成图论做的，对于每一个数字作一条有向边连向它的倍数，然后遍历一遍这张图，找出最长的链，最终由于复杂度太高而TLE。当一道题一下子没有思路的时候，不妨看看它的数据范围。这题中集合元素大小1<=ai<=1e6，也就是说我们可以记录每一个1e6以内的数字是否出现过。然后利用倍增法查找，比如3、6、9、12的找。如果某个正好倍增到某个出现过的数字，那么当前这个位置及其之前的最长子序列dp[ai * k]为该点已经记录的序列长度dp[ai * k]或 用于倍增数字的序列长度dp[ai]加上1，不断更新，最终遍历一遍集合中以所有元素为结尾的子序列，找到最大值就可以了。

——Code——

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int n;
int a[1000006];
int dp[1000006];
int pos[1000006];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	{
		dp[i]=1;
		scanf("%d", &a[i]);
		pos[a[i]]=i;
	}
	for(int i=1;i<=n;++i)
	{
		for(int j=2*a[i];j<=a[n];j+=a[i])
		{
			int k=pos[j];
			if( k==0 ) continue;
			dp[k]=max(dp[k], dp[i]+1);
		}
	}
	int ans=0;
	for(int i=1; i<=n; ++i)
		ans=max(ans, dp[i]);
	printf("%d\n", ans);
	return 0;
} 

B - Geometric Progression （*1700）

——题意——
和上题类似，给出一个长度为n的序列{an}，和一个基数k，找出序列中所有长度为三的序列，满足三个元素呈等比关系，公比为k。其中，序列长度1<=n<=2e5，公比1<=k<=2e5，序列元素-1e9<=ai<=1e9。

——题解——
由题中数据范围可以分析出，2e9范围内只有2e5个元素，并且可重复，说明序列中的数字很“ 稀疏 ”，可以考虑用map来记录每个数字出现的次数cnt[ai]。对于序列中的一个数字ai，它所确定的三元序列数即为它左边值为ai/k的个数乘以右边值为ai * k的个数。

——Code——

#include<iostream>
#include<map> 
#include<cstdio>
#include<algorithm>
using namespace std;
map<long long,long long> cntl,cntr;
int n;
long long k;
int a[200005];
int main()
{
	scanf("%d %lld",&n,&k);
	for(int i=1;i<=n;++i)
	{
		scanf("%lld",&a[i]);
		++cntr[a[i]];
	}
	long long ans=0;
	for(int i=1;i<=n;++i)
	{
		--cntr[a[i]];
		if(!(a[i]%k)) ans+=cntl[a[i]/k]*cntr[a[i]*k];
		++cntl[a[i]];
	}
	printf("%lld\n",ans);
	return 0;
}

C - Bear and Blocks （*1800）

——题意——
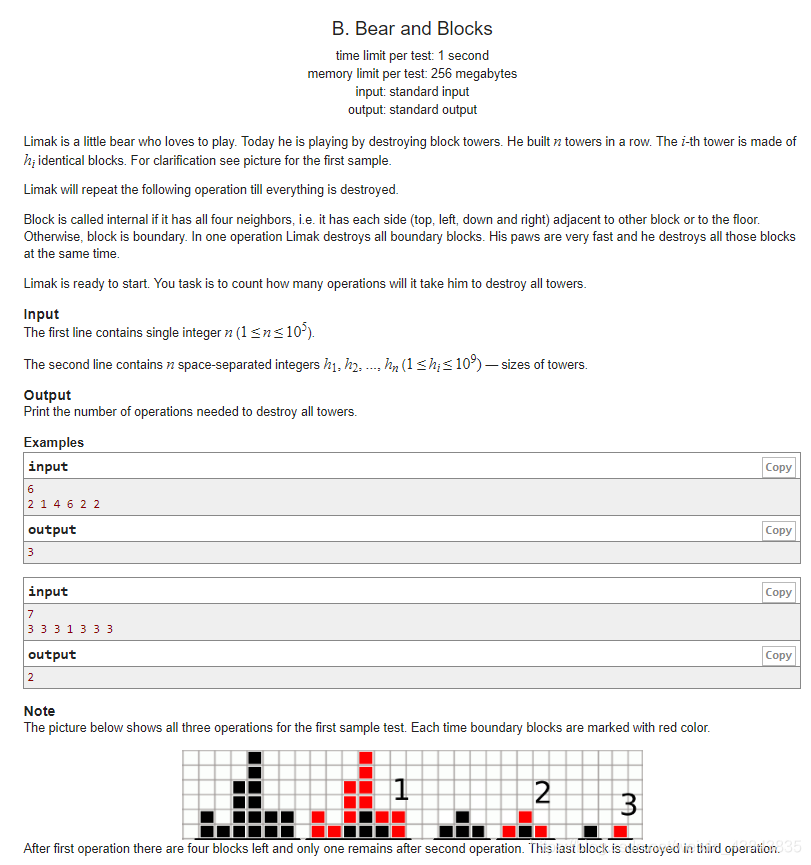
给出一个长度为n的序列{hn}，hi代表积木的高度，每次只有上左右都有积木的积木无法被破坏，其它积木都会被Bear在一回合内破话，问这些积木几回合被全部破坏。其中1<=n<=1e5，1<=hi<=1e9.

——题解——
这是一道挺有意思的思维题，关键在于怎么表达出破坏积木这一过程。实际上，可以把破坏看成两个部分，从左到右和从右到左，即先从左到右移除一些积木，在从右到左移除一些方块。破坏次数即为前者被破坏的次数加1和自身高度中的较小者，即dp[i]=min(dp[i-1]+1,h[i])，从右和从左各进行一次。

——Code——

#include<iostream>
#include<cstdio>
using namespace std;
int n;
int h[100005];
int dp[100005];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
		scanf("%d",&h[i]);
	for(int i=1;i<=n;++i)
		dp[i]=min(h[i],dp[i-1]+1);
	for(int i=n;i>=1;--i)
		dp[i]=min(dp[i],dp[i+1]+1);
	int ans=-1;
	for(int i=1;i<=n;++i)
		ans=max(dp[i],ans);
	printf("%d\n",ans);
	return 0;
}