1.一维卡尔曼滤波(恒定的动态模型)
2.一维卡尔曼滤波(动态模型)
3.二维-卡尔曼滤波算法
使用范围:恒定的动态模型
例如:测量一枚硬币的直径,一栋建筑的高度
1.求平均值
通常我们求一个测量值,都是测量大量数据,然后取它的平均值
X k = 1 k ( Z 1 + Z 2 + . . . + Z k ) X_k = \frac{1}{k}(Z_1+Z_2+...+Z_k) Xk=k1(Z1+Z2+...+Zk)
上面的公式可以转化为 转化过程视频讲解
X
k
=
X
k
−
1
+
1
k
(
Z
k
−
X
k
−
1
)
X_k = X_{k-1} + \frac{1}{k}(Z_k - X_{k-1} )
Xk=Xk−1+k1(Zk−Xk−1)
可以把公式写作成,
X
k
=
X
k
−
1
+
K
k
(
Z
k
−
X
k
−
1
)
X_k = X_{k-1} + K_k(Z_k - X_{k-1} )
Xk=Xk−1+Kk(Zk−Xk−1) 这个才是我们要的主要公式
K
k
K_k
Kk :表示卡尔曼增益
需要引入两个系数: e E S T e_{EST} eEST(估计误差) 和 e M E A e_{MEA} eMEA(测量误差),这两个系数的初始值是知道的,
e
E
S
T
e_{EST}
eEST(估计误差) :初始值可以随便给一个数,因为估计误差会在每次计算中迭代更新
e
M
E
A
e_{MEA}
eMEA(测量误差):例如一把尺子的精度是3mm,那么
e
M
E
A
=
3
e_{MEA} = 3
eMEA=3(固定值)
卡尔曼增益的计算方法
K k = e E S T k − 1 e E S T k − 1 + e M E A K_k = \frac{e_{ESTk-1}}{e_{ESTk-1} + e_{MEA}} Kk=eESTk−1+eMEAeESTk−1
e E S T k = ( 1 − K k ) e E S T k − 1 e_{ESTk} = (1 - K_k) e_{ESTk-1} eESTk=(1−Kk)eESTk−1
| 测量值 | 估计值 | 估计误差 | 测量误差 | 卡尔曼增益 |
|---|---|---|---|---|
| Z k Z_k Zk | X k X_k Xk | e E S T e_{EST} eEST | e M E A e_{MEA} eMEA | K k K_k Kk |
例如采集一枚直径为50mm的硬币
示例代码kalman.c
#include <stdio.h>
#include <stdlib.h>
#include <ctime>
/**************************************** */
#define KALMAN_DATA_NUM 100 // 采集数据的数量
/**************************************** */
typedef struct
{
int Z_k[KALMAN_DATA_NUM]; // 测量值
char E_mea; // 测量误差
double X_k[2]; // 估算值
double E_est; // 估计误差
} Kalman_InitDef;
Kalman_InitDef Kalman_Structure;
/**
* @brief 计算Kk(卡尔曼增益)
*
* @param E_est 上一个估计误差
* @param E_mea 测量误差
* @return float
*/
double Kalman_Gain_Calculation(double E_est, double E_mea)
{
double result;
result = E_est / (E_est + E_mea);
return result;
}
/**
* @brief 生成随机数 %7 产生0到6,加上47得到47到53
*
*/
void Generating_Random_Masurement(void)
{
int i;
srand(time(NULL)); // 初始化随机数生成器
for (i = 0; i < KALMAN_DATA_NUM; i++)
{
/*************************************************************************** */
// if (i % 50 == 0)
// Kalman_Structure.Z_k[i] = rand() % 7 + 67;
// else
// Kalman_Structure.Z_k[i] = rand() % 7 + 47;
/*************************************************************************** */
// if (i > 50)
// Kalman_Structure.Z_k[i] = rand() % 7 + 67;
// else
// Kalman_Structure.Z_k[i] = rand() % 7 + 47;
/*************************************************************************** */
// Kalman_Structure.Z_k[i] = rand() % 7 + 47 + i;
/*************************************************************************** */
Kalman_Structure.Z_k[i] = rand() % 7 + 47;
/*************************************************************************** */
}
// printf("Z_K******************************\n\n\n");
}
void Kalman_Parameter_Init(void)
{
Kalman_Structure.X_k[0] = 40;
Kalman_Structure.E_est = 100;
Kalman_Structure.E_mea = 9;
}
void Kalman_X_K_Calculation()
{
int tb_data = Kalman_Structure.Z_k[0];
int count = 0;
int absolute;
int i;
double Kalman_Gain;
for (i = 1; i < KALMAN_DATA_NUM; i++)
{
Kalman_Gain = Kalman_Gain_Calculation(Kalman_Structure.E_est, Kalman_Structure.E_mea);
Kalman_Structure.X_k[1] = Kalman_Structure.X_k[0] + Kalman_Gain * (Kalman_Structure.Z_k[i] - Kalman_Structure.X_k[0]);
Kalman_Structure.E_est = ((double)1 - Kalman_Gain) * Kalman_Structure.E_est;
Kalman_Structure.X_k[0] = Kalman_Structure.X_k[1];
printf("Z_k=%d , X_k=%0.2f , Kk=%0.3f , E_est=%0.3f\n",
Kalman_Structure.Z_k[i],
Kalman_Structure.X_k[1],
Kalman_Gain,
Kalman_Structure.E_est);
}
}
int main()
{
Kalman_Parameter_Init();
Generating_Random_Masurement();
Kalman_X_K_Calculation();
system("pause"); // 暂停运行
}
示例代码kalman.c
#include <stdio.h>
#include <stdlib.h>
#include <ctime>
/**************************************** */
#define KALMAN_DATA_NUM 200 // 采集数据的数量
/**************************************** */
typedef struct
{
float Last_P; // 上次估算协方差 不可以为0
float Now_P; // 当前估算协方差
float out; // 卡尔曼滤波器输出
float Kg; // 卡尔曼增益
float Q; // 过程噪声协方差
float R; // 观测噪声协方差
} Kalman;
Kalman kfp;
void Kalman_Init()
{
kfp.Last_P = 3;
kfp.Now_P = 0;
kfp.out = 0;
kfp.Kg = 0;
kfp.Q = 0;
kfp.R = 3;
}
/**
*卡尔曼滤波器
*@param Kalman *kfp 卡尔曼结构体参数
* float input 需要滤波的参数的测量值(即传感器的采集值)
*@return 滤波后的参数(最优值)
*/
float KalmanFilter(Kalman *kfp, float input)
{
// 预测协方差方程:k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
kfp->Now_P = kfp->Last_P + kfp->Q;
// 卡尔曼增益方程:卡尔曼增益 = k时刻系统估算协方差 / (k时刻系统估算协方差 + 观测噪声协方差)
kfp->Kg = kfp->Now_P / (kfp->Now_P + kfp->R);
// 更新最优值方程:k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * (测量值 - 状态变量的预测值)
kfp->out = kfp->out + kfp->Kg * (input - kfp->out); // 因为这一次的预测值就是上一次的输出值
// 更新协方差方程: 本次的系统协方差付给 kfp->LastP 威下一次运算准备。
kfp->Last_P = (1 - kfp->Kg) * kfp->Now_P;
return kfp->out;
}
int main()
{
int Z_k = 0;
srand(time(NULL)); // 初始化随机数生成器
Kalman_Init();
for (int i = 0; i < KALMAN_DATA_NUM; i++)
{
Z_k = rand() % 7 + 47; // 50±3随机数
KalmanFilter(&kfp, Z_k);
printf("Z_k=%d , X_k=%0.2f , Kk=%0.3f , E_est=%0.3f\n",
Z_k,
kfp.out,
kfp.Kg,
kfp.Last_P);
}
system("pause"); // 暂停运行
}
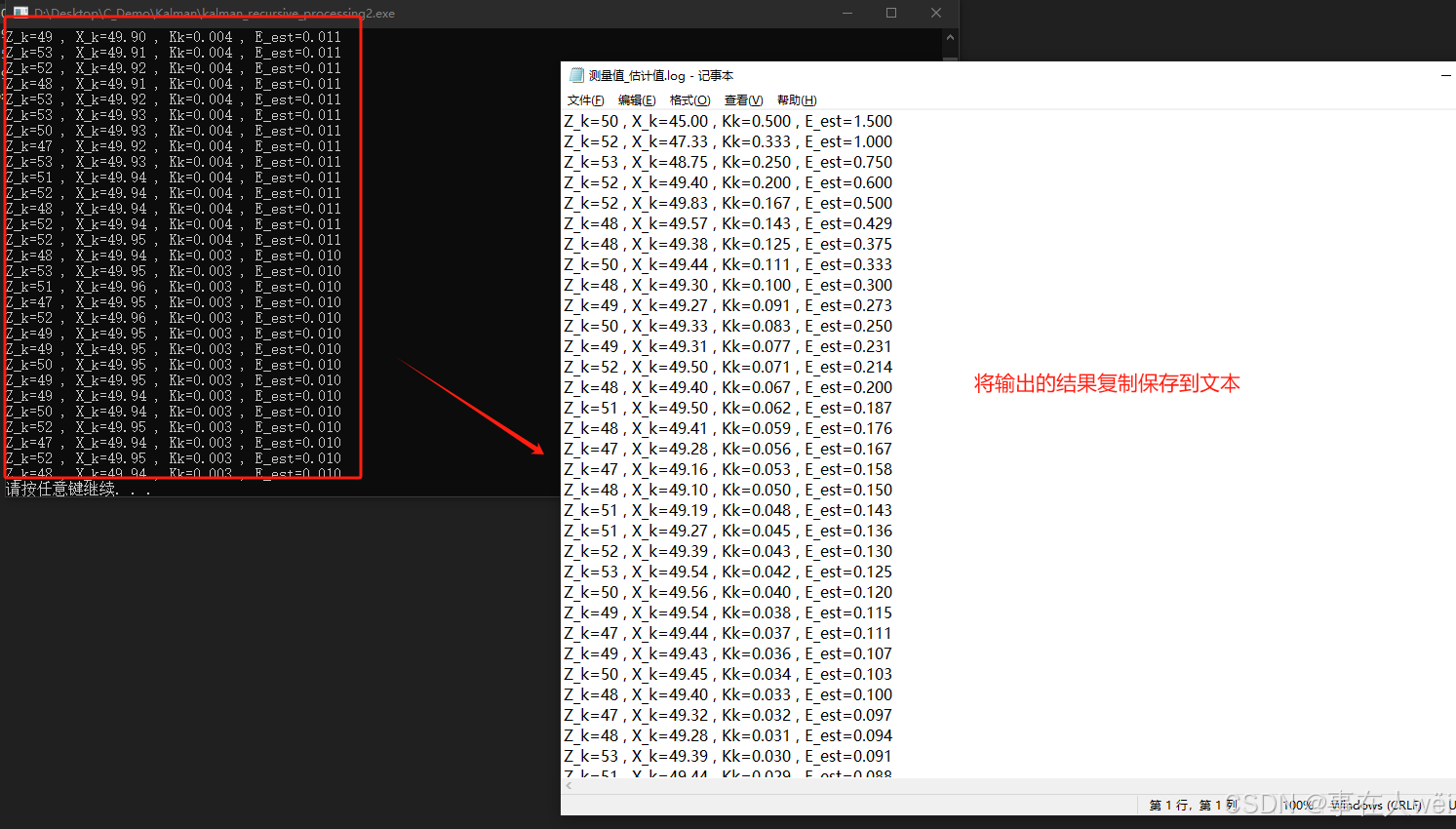
python脚本,主要用来将数据转化成图形
kalman.py
import re
import matplotlib.pyplot as plt
from tkinter import filedialog
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为黑体
# 创建一个图形和主轴
fig, ax = plt.subplots(figsize=(15, 6))
fig.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.95)
# 新建一个图形用于显示Kk和E_est
fig2, ax2 = plt.subplots(figsize=(15, 6))
fig2.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.95)
ax2.set_title("卡尔曼增益与估计误差变化趋势")
ax2.set_xlabel("样本点")
ax2.set_ylabel("值")
if __name__ == '__main__':
file_path = filedialog.askopenfilename(
title="请选择数据", filetypes=[("log files", "*.log"), ("txt files", "*.txt")])
print('您选择的文件路径是:', file_path)
# 窗口大小
window_size = 10
while True:
# 打开并读取文件
with open(file_path, 'r') as file:
# 初始化列表
Z_k_list = [] # 测量值
X_k_list = [] # 估计值
average_Z_k_list = [] # 测量值_平均值
Kk_list = [] # 卡尔曼增益
E_est_list = [] # 估计误差
for line in file:
# 使用正则表达式提取Z_k的值
match_zk = re.search(r'Z_k=(\d+)', line)
if match_zk:
Z_k = int(match_zk.group(1))
Z_k_list.append(Z_k)
# 使用正则表达式提取X_k的值
match_xk = re.search(r'X_k=(\d+\.\d+)', line)
if match_xk:
X_k = float(match_xk.group(1))
X_k_list.append(X_k)
# 提取Kk的值
match_kk = re.search(r'Kk=(\d*\.(\d{3}))', line)
if match_kk:
Kk = float(match_kk.group(1))
Kk_list.append(Kk)
# 提取E_est的值
match_ee = re.search(r'E_est=(\d*\.(\d{3}))', line)
if match_ee:
E_est = float(match_ee.group(1))
E_est_list.append(E_est)
# 计算每10个数据的平均值,并填充到average_Z_k_list
index = 0
while index < len(Z_k_list):
# 获取当前窗口的数据
window = Z_k_list[index:index + window_size]
# 计算当前窗口的平均值
if window:
average = sum(window) / len(window)
# 将平均值重复填充到average_Z_k_list中
average_Z_k_list.extend(
[average] * min(window_size, len(Z_k_list) - index))
index += window_size
# 清理上一次的图像
ax.clear()
ax2.clear()
x_data = range(len(Z_k_list))
x_data2 = range(len(Kk_list)) # Kk和E_est的x轴数据
# 绘制两个数据集
p1, = ax.plot(x_data, Z_k_list, 'b.--', color="C0", label="采集数据")
p2, = ax.plot(x_data, X_k_list, 'r.--', color="C1", label="卡尔曼滤波")
p3, = ax.plot(x_data, average_Z_k_list, 'g.-',
color="C2", label="采集10个点平均值")
# 添加真实值
ax.axhline(y=50, color='r', linestyle='-', label="真实值")
# 添加图例
ax.legend(handles=[p1, p2, p3])
# 设置标题
ax.set_title("卡尔曼滤波 测量值&估计值比较")
ax.set_xlabel("样本点")
ax.set_ylabel("值")
# 在新窗口中绘制Kk和E_est
p4, = ax2.plot(x_data2, Kk_list, 'b.', label="卡尔曼增益")
p5, = ax2.plot(x_data2, E_est_list, 'r.', label="估计误差")
# 添加图例
ax2.legend(handles=[p4,p5])
# 显示图形
plt.pause(0.1)
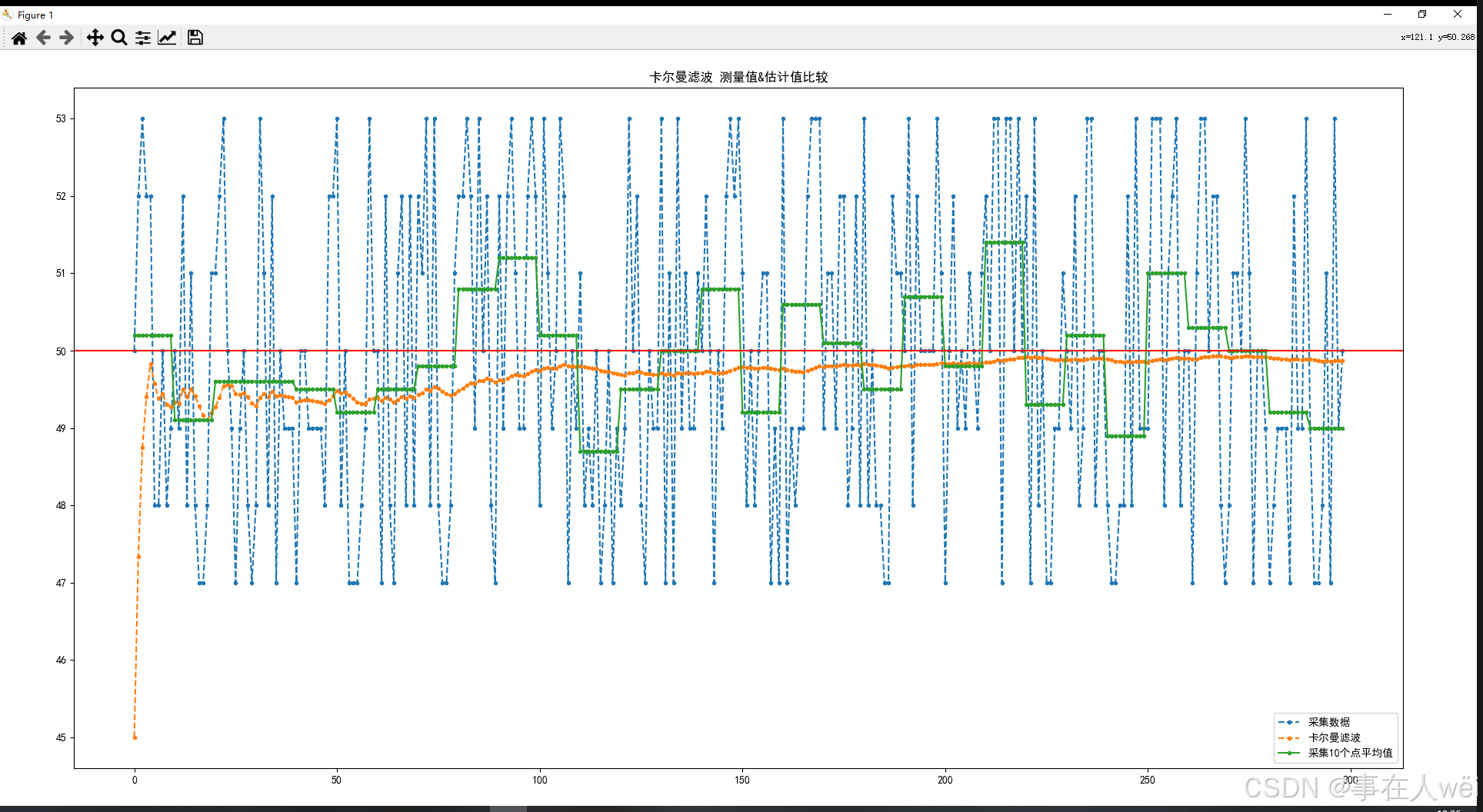
运行上面的python脚本,选择文本,就可以输入下面的图像
相比于求平均值,卡尔曼滤波更接近真实值
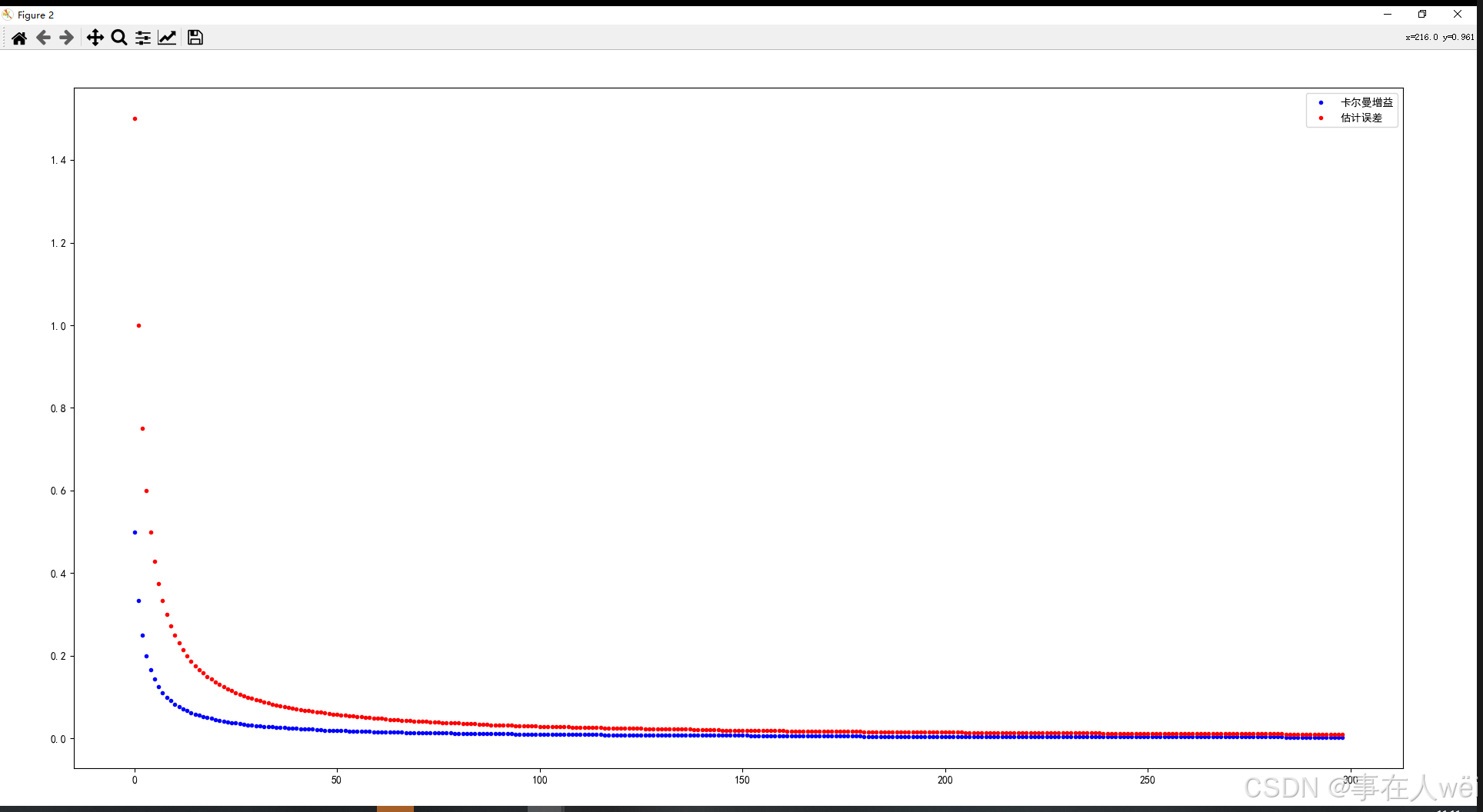
随着每次迭代
e
E
S
T
e_{EST}
eEST(估计误差)
K
k
K_k
Kk (卡尔曼增益)会越来越小
问题: 如果测量的不是恒定的参数,例如:温度逐渐上升
在示例代码kalman.c中,将随机数修改成(模拟温度逐渐上升)
Z_k = rand() % 7 + 47 + i; // 50±3随机数
得到的效果是这样
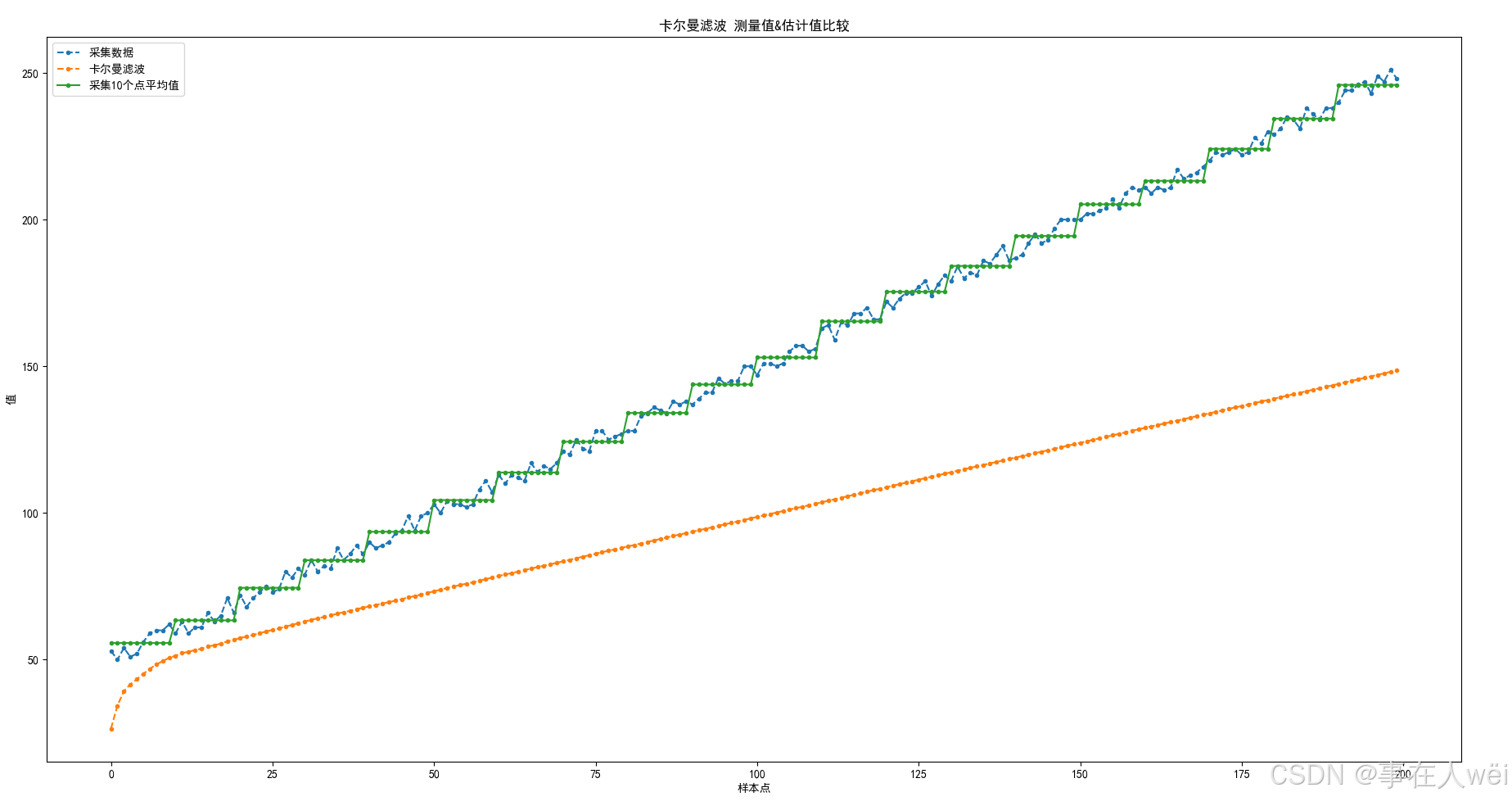
发现卡尔曼滤波的结果跟不上实际的变化,不知道怎么处理…
欢迎评论区交流学习,或者私聊我
答:这个问题已经解决,可以参考2.一维卡尔曼滤波(动态模型)
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








