排序算法详解<3>

着里说两种，用二叉树的性质来表示的排序方法，分别是堆排序和归并排序。

1. 堆排序
   堆排序就是利用堆（假设利用大顶堆）进行排序的方法。他的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的n-1个序列从新构造成一个堆，这样就会得到n个元素中的次小值。如此反复执行，便能得到一个有序序列了。
   图示为：
   代码示例：

//堆排序
void HeapAdjust(int *a, int s, int m)
{
 int temp, j;
 temp = a[s];
 for (j = 2 * s; j <= m; j *= 2)//沿关键字较大的孩子结点向下筛选 
 {
  if (j < m && a[j] < a[j + 1])
   ++j;      //j为关键字中较大的记录的下标
  if (temp >= a[j])
   break;
  a[s] = a[j];
  s = j;
 }
 a[s] = temp;
}
void HeapSort(int* a,int len)
{
 int i;
 for (i = len / 2; i > 0; i--)//把当前序列排序为大顶堆
 {
  HeapAdjust(a, i, len);
 }
 for (i = len-1; i > 0; i--)
 {
  Swap(&a[0], &a[i]);//将堆顶记录和当前子序列的最后一个元素交换
  HeapAdjust(a, 0, i - 1);//把除最后一个元素的子序列从新调整为大顶堆
 }
}

堆排序是一种不稳定的排序算法，它的时间复杂度为O(n㏒n)，空间复杂度为O(1).

2. 归并排序
   归并排序就是利用归并的思想实现的排序算法。它的原理是假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到（n/2）（【x】表示不小于x的最小整数）个长度为2或1的有序子序列；再两两归并，……，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。
   图示为：
   
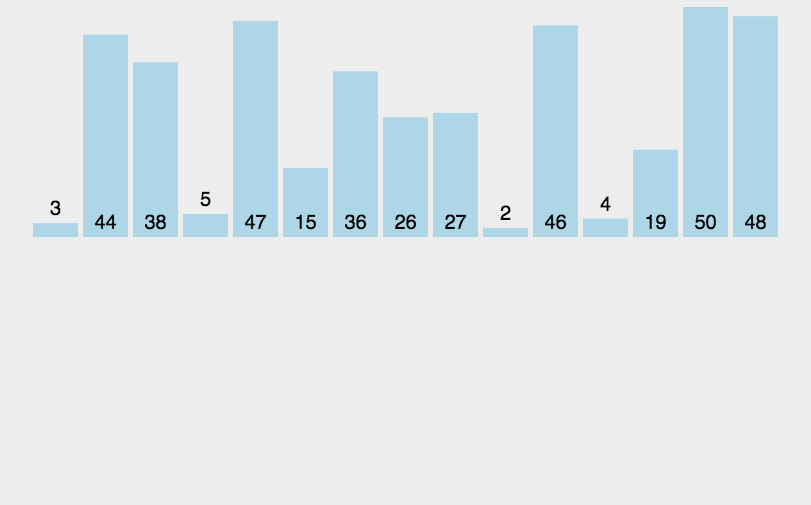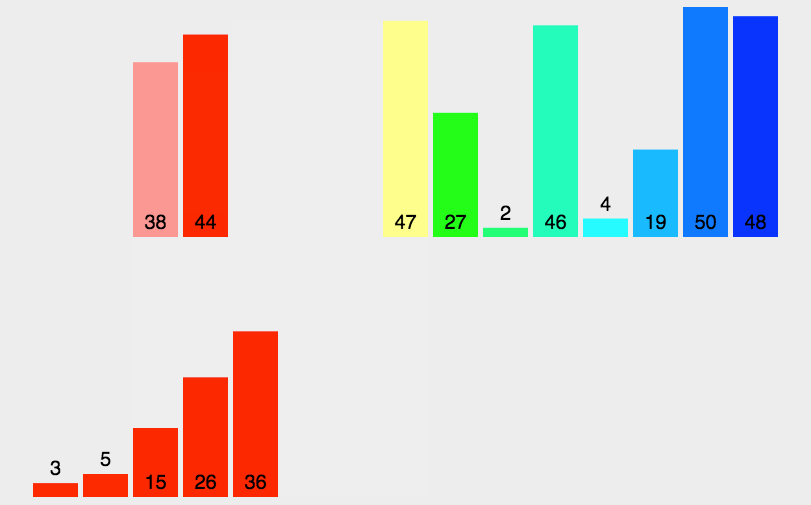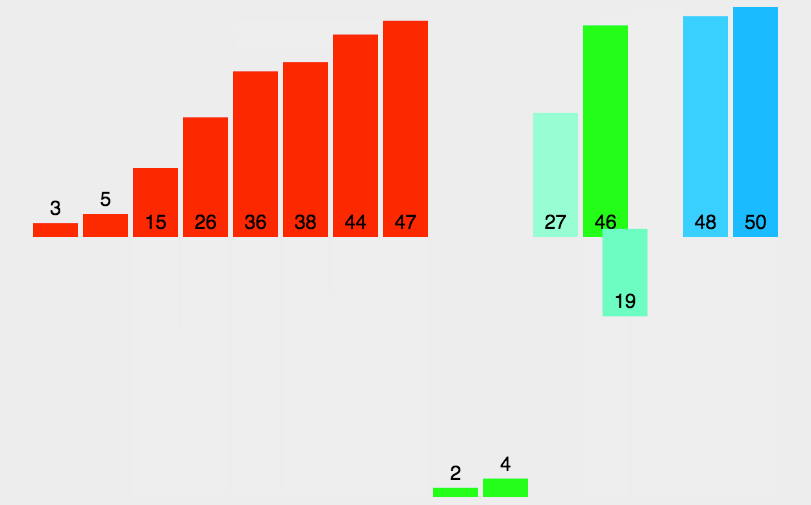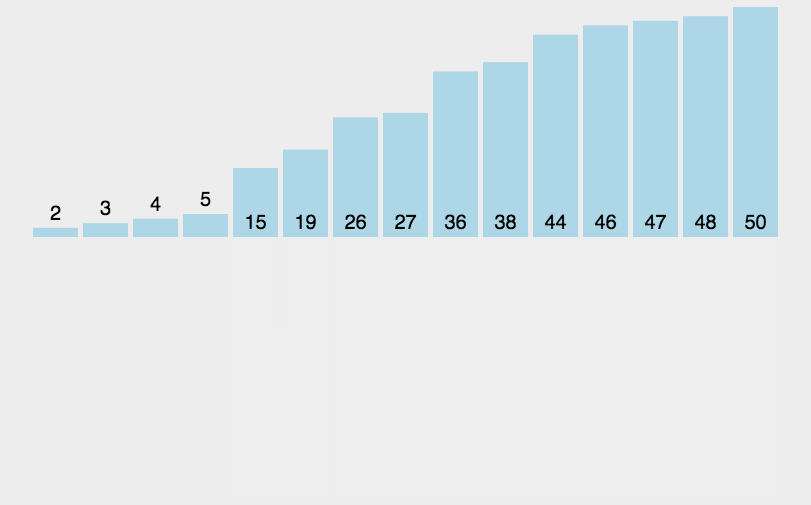
   代码表示为：

//归并排序
void merge(int* src, int* des, int low, int high, int mid)
{
 int i = low;
 int k = low;
 int j = mid + 1;
 while ((i <= mid) && (j <= high))
 {
  //排序，把小的依次放入des数组中
  if (src[i] < src[j])
  {
   des[k++] = src[i++];
  }
  else
  {
   des[k++] = src[j++];
  }
 }
 while (i <= mid)
 {
  des[k++] = src[i++];
 }
 while (j <= high)
 {
  des[k++] = src[j++];
 }
}
void M_Sort(int* src, int* des, int low, int high, int max_size)
{
 int mid = (low + high) / 2;
 //判断此时每个小块中的元素是否为1个；
 if (low == high)
 {
  des[low] = src[low];
 }
 else
 {
  int mid = (low + high) / 2;
  int* des_space = (int*)malloc(sizeof(int)*max_size);
  if(NULL != des_space)
  {
   //递归分：把一个数组不断从中分开 ，直到分为一个元素一个快
   M_Sort(src, des_space, low, mid, max_size);
   M_Sort(src, des_space, mid + 1, high, max_size);
   //合并，把分开的元素按反向合并，并排序
   merge(des_space, des, low, high, mid);
  }
  free(des_space);//释放用malloc开辟的空间
 }
}
void Merge_Sort(int* a, int low, int high, int len)
{
 M_Sort(a, a, low, high, len);
}

归并排序是一个稳定的排序算法，在归并排序中，大部分工作是在解决/归并的步骤中完成的，因为分解步骤并没有真正执行任何操作（视为O（1））。
当我们称之为归并的（a，低，中，高）时候，我们处理k =（高 - 低+ 1）项。 最多会有 k-1 个比较。 从原始数组 a 到临时数组 b 有 k 个移动，而另一个 k 移回。 总的来说，归并子例程内的操作次数 <3k-1 = O（k）。
主函数再次不做解释，自己根据自己的要求自己写主函数；