一,二叉树的中序非递归遍历(借助顺序栈实现)
1.完整代码
#include<iostream>
#include<malloc.h>
using namespace std;
#define TElemType int
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
typedef BiTree SElemType; //定义栈元素为二叉树的指针类型
typedef int Status;
#define STACK_INIT_SIZE 10 //存储空间初始分配量
#define STACK_INCREMENT 2 //存储空间分配增量
typedef struct SqStack
{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;
/****************基本操作函数 ****************/
//构建一个空栈并初始化
void InitStack(SqStack &S)
{
S.base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if (!S.base)
exit(OVERFLOW);
S.top = S.base; //栈顶指向栈底,空栈
S.stacksize = STACK_INIT_SIZE; //存储空间为初始分配量
}
//判断栈空
Status StackEmpty(SqStack S)
{
if (S.top == S.base) //空栈条件
return TRUE;
else
return FALSE;
}
//压栈, 插入元素为e的新的栈顶元素
void Push(SqStack &S, SElemType e)
{
if (S.top - S.base == S.stacksize) //栈满,追加空间
{
S.base = (SElemType *)realloc(S.base, (S.stacksize + STACK_INCREMENT) * sizeof(SElemType));
if (!S.base)
exit(OVERFLOW);
S.top = S.base + S.stacksize; //修改栈顶指针,指向新的栈顶
S.stacksize += STACK_INCREMENT; //更新当前已分配的存储空间
}
*(S.top++) = e; //e入栈,成为新的栈顶元素,栈顶指针上移
}
//出栈
Status Pop(SqStack &S, SElemType &e)
{
if (S.top == S.base)
return ERROR;
e = *--S.top; //栈顶指针下移一个存储单元, 将栈顶元素赋值给e
return OK;
}
//先序创建二叉树
int CreateBiTree(BiTree &T)
{
TElemType a;
scanf("%d", &a);
if ( 0 == a ) //输入结点的值,0为空
{
T = NULL; //结点为空
}
else
{
T = (BiTree)malloc(sizeof(BiTNode)); //生成根结点
if ( !T )
exit(OVERFLOW);
T->data = a; //将值赋给T所指结点
CreateBiTree(T->lchild); //递归构造左子树
CreateBiTree(T->rchild); //递归构造右子树
}
return OK;
}
//非递归中序遍历二叉树,借助栈实现
Status InOrderTraverse(BiTree T)
{
SqStack S;
BiTree p;
InitStack(S);
p = T;
while( p || !StackEmpty(S) ) //二叉数不空或栈不空
{
if ( p ) //二叉树不空
{
Push(S, p); //根指针入栈
p = p->lchild; //p指向其左孩子
}
else
{
Pop(S, p); //根指针出栈
printf("%d ", p->data); //输出根结点的数据
p = p->rchild; //p指向其右孩子
}
}
return OK;
}
/****************主函数 ****************/
int main()
{
BiTree T = NULL;
cout << "请按照先序遍历输入二叉树('0'无): ";
CreateBiTree(T);
cout << "中序遍非递归遍历: ";
InOrderTraverse(T);
printf("\n");
return 0;
}
2.测试结果
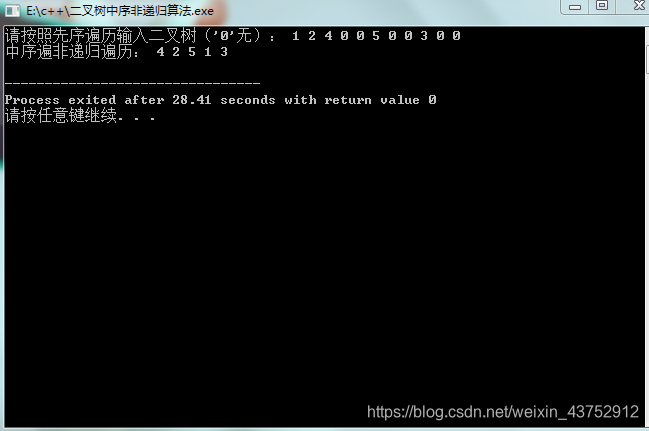
二. 二叉树的层次遍历(借助循环队列实现)
1.完整代码
#include<iostream>
#include<malloc.h>
using namespace std;
#define TElemType int
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define MAXQSIZE 100 //最大队列长度
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
typedef BiTree QElemType; //定义队列元素为二叉树的指针类型
typedef int Status;
typedef struct{
QElemType *base;
int front; //头指针,若队列不空,指向队列头元素
int rear; //尾指针,若若队列不空,指向队列尾元素的下一个位置
}SqQueue;
/********************基本功能函数**********************/
//队列的初始化
Status InitQueue(SqQueue &Q)
{
Q.base = new QElemType[MAXQSIZE]; //分配数组空间
if ( !Q.base ) //存储分配失败
exit(OVERFLOW);
Q.front = Q.rear = 0; //头指针尾指针置零,队列为空
return OK;
}
//队列的入队
Status EnQueue(SqQueue &Q, QElemType e)
{
if ((Q.rear + 1) % MAXQSIZE == Q.front) //队列内元素已满
return ERROR;
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE; //队尾指针+1
return OK;
}
//队列的出队
Status DeQueue(SqQueue &Q, QElemType &e)
{
if ( Q.front == Q.rear) //队空
return ERROR;
e = Q.base[Q.front]; //保存队头元素
Q.front = (Q.front + 1) % MAXQSIZE; //队头指针+1
}
//判断队列是否为空
Status QueueEmpty(SqQueue Q)
{
if ( Q.front == Q.rear)
return true;
else
return false;
}
//先序创建二叉树
int CreateBiTree(BiTree &T)
{
TElemType a;
scanf("%d", &a);
if ( 0 == a ) //输入结点的值,0为空
{
T = NULL; //结点为空
}
else
{
T = (BiTree)malloc(sizeof(BiTNode)); //生成根结点
if ( !T )
exit(OVERFLOW);
T->data = a; //将值赋给T所指结点
CreateBiTree(T->lchild); //递归构造左子树
CreateBiTree(T->rchild); //递归构造右子树
}
return OK;
}
//二叉树的层次遍历
void LevelOrder(BiTree T)
{
BiTree p = T;
SqQueue q;
InitQueue(q); //初始化队列
EnQueue(q, p); //根结点指针入队
while( !QueueEmpty(q) ) //队列不空,则循环
{
DeQueue(q, p); //出队结点p
printf("%d ", p->data); //访问结点p
if(p->lchild != NULL)
EnQueue(q, p->lchild); //有左孩子时将其入队
if(p->rchild != NULL)
EnQueue(q, p->rchild); //有右孩子时将其入队
}
}
/****************主函数 ****************/
int main()
{
BiTree T = NULL;
cout << "请按照先序遍历输入二叉树('0'无): ";
CreateBiTree(T);
cout << "二叉树层次遍历结果: ";
LevelOrder(T);
printf("\n");
return 0;
}
2.测试结果
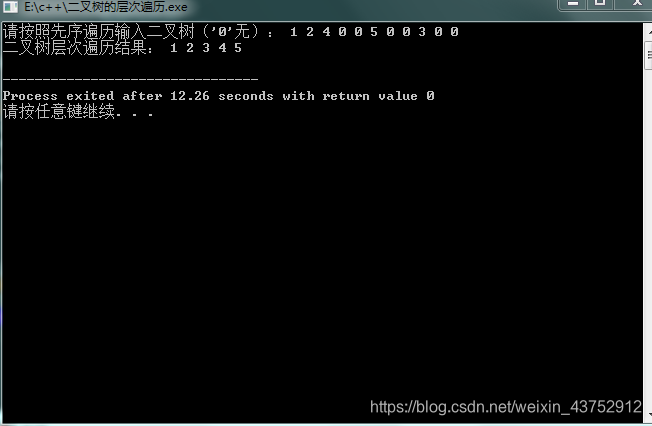





 本文详细介绍了二叉树的中序非递归遍历和层次遍历算法,通过顺序栈和循环队列实现,提供了完整的C++代码示例及测试结果。
本文详细介绍了二叉树的中序非递归遍历和层次遍历算法,通过顺序栈和循环队列实现,提供了完整的C++代码示例及测试结果。
















 1199
1199

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








