Codeforces Round #651 (Div. 2)(ABCDE题解)-优快云博客

在这里插入图片描述
题面大意：
给你一个 $n$ ，要你找两个数 $a, b (a < b < = n)$ ，求 $m a x (g c d (a, b))$ 。
思路：
直接取 $b = n$ ，然后 $a = n / 2$ 就行了，所以答案是 $n / 2$ ，如果为奇数 $n - -$ 。
代码：

#include<iostream>
using namespace std;

void solved(){
    int n;cin>>n;
    if(n & 1)n--;
    cout<<(n/2)<<endl;
}
int main(){
    int t;cin>>t;
    while(t--) solved();
    return 0;   
}

在这里插入图片描述

题面大意：
给你 $2 n$ 个数，要你选 $2 n - 2$ 个数，每次选两个 $a, b$ ,把他们的和加入到新的序列中，要你使得新的序列 $g c d (a i, a j) > 1$ ，要你输出你的选择的方法。
思路：
令 $g c d (a, b) = 2$ 。
把奇数和偶数分开，偶+偶=偶，奇+奇=偶， $g c d (偶，偶) > = 2$ 。
然后输出一下就行了。
代码：

#include<iostream>
#include<vector>
using namespace std;
/*
5
2 4 6 8 10 2 4 6 8 10
*/
void solved(){
    int N;cin>>N;
    vector<int>v1;
    vector<int>v2;
    for(int i = 1; i <= 2 * N; i++){
        int x;cin>>x;
        if(x & 1)v1.push_back(i);
        else v2.push_back(i);
    }
    int n = v1.size();
    int m = v2.size();
    int cnt = 2 * N - 2;
    if(n > m){
        if(n & 1)n--;
        for(int i = 0;cnt > 0 && i < n; i += 2,cnt -= 2){
            cout<<v1[i]<<" "<<v1[i + 1]<<endl;
        }
        for(int i = 0;cnt > 0 && i < m; i += 2,cnt -= 2){
            cout<<v2[i]<<" "<<v2[i + 1]<<endl;
        }
    }else{
        if(m & 1)m--;
        for(int i = 0;cnt > 0 && i < m; i += 2,cnt -= 2){
            cout<<v2[i]<<" "<<v2[i + 1]<<endl;
        }
        for(int i = 0;cnt > 0 && i < n; i += 2,cnt -= 2){
            cout<<v1[i]<<" "<<v1[i + 1]<<endl;
        }

    }
}
int main(){
    int t;cin>>t;
    while(t--) solved();
    return 0;
}

在这里插入图片描述

题面大意：
给你一个数 $n$ ，你可以对他 $- 1$ ，或者 $n / x$ ,其中 $x$ 是 $n$ 的奇因子，两个人博弈，直到一个人不能进行操作为止，问你谁胜。
思路：
首先我们看几个显然的状态。
$n = 1$ ，先手必败。
$n = 2$ ，先手必胜。
$n = 3$ ，先手必胜。
$n = 4$ ，先手必败。
我们可以发现，当 $n$ 是奇数的时候，直接除上本身，先手必胜。
当 $n$ 是偶数的时候就比较麻烦，我们可以质因数分解为两种情况。 $n=2^k*p,$ 或者 $n=2^k$ 。
首先看 $n=2^k$ ，当 $k = 1$ ，先手必胜，当 $k > 1$ ，先手必败。
然后看 $n=2^k*p$ ，当 $k = 1$ ，如果 $p$ 不能再分解了，那么只能是先手必败，如果可以分解为 $p = a * b * c$ ，那么先手先除去 $b c,$ 则 $p = 2 * a$ ,这样先手必胜。
如果 $k > 1$ ，只要有质因数 $p$ ，直接除 $p$ ，则 $n=2^k$ ,这样先手必胜。如果没有质因子，先手必败。
代码：

#include<iostream>
using namespace std;

typedef long long int ll;
void first(){
    cout<<"Ashishgup"<<endl;
}
void second(){
    cout<<"FastestFinger"<<endl;
}
void solved(){
    ll n;cin>>n;
    if(n == 1){cout<<"FastestFinger"<<endl;return ;}
    if(n == 2){cout<<"Ashishgup"<<endl;return ;}
    if(n & 1){cout<<"Ashishgup"<<endl;return ;}
    int k = 0,p = 0;
    while(n % 2 == 0){
        n /= 2;
        k++;
    }
    for(int i = 3; i * i <= n; i++){
        while(n % i == 0){
            n /= i;
            p++;
        }
    }
    if(n > 1)p++;
    if(k == 1){
        if(p == 1){
            second();
        }else{
            first();
        }
    }else{
        if(p){
            first();
        }else{
            second();
        }
    }
}
int main(){
    int t;cin>>t;
    while(t--) solved();
    return 0;
}

在这里插入图片描述

题面大意：
给你一个长度为 $n$ 的序列，要你找到 $f = m i n (m a x (a 2, a 4, . . a 2 n), m a x (a 1, a 3, a 2 n + 1))$ 。
思路：
答案越大，越容易满足，我们二分这个答案，枚举把 $最小值$ 在偶数或者奇数序列中枚举出来，满足一个就行了， $c h e c k$ 按照题目要求模拟一下就行了。
代码：

#include<iostream>
using namespace std;

typedef long long int ll;
const int maxn = 2e5 + 10;
int a[maxn];
int n,k;
bool check(int mid,int flag){
    int cnt = 0;
    for(int i = 1; i <= n; i++){
        if(flag || a[i] <= mid){
            flag ^= 1;
            cnt++;
        }
    }
    return cnt >= k;
}
void solved(){
    cin>>n>>k;
    for(int i = 1; i <= n; i++)cin>>a[i];
    int l = 1,r = 1e9;
    int ans;
    while(l <= r){
        int mid = l + r >> 1;
        if(check(mid,0) || check(mid,1)){
            ans = mid;
            r = mid - 1;
        }else{
            l = mid + 1;
        }
    }
    cout<<ans<<endl;

}
int main(){
    solved();
    return 0;
}

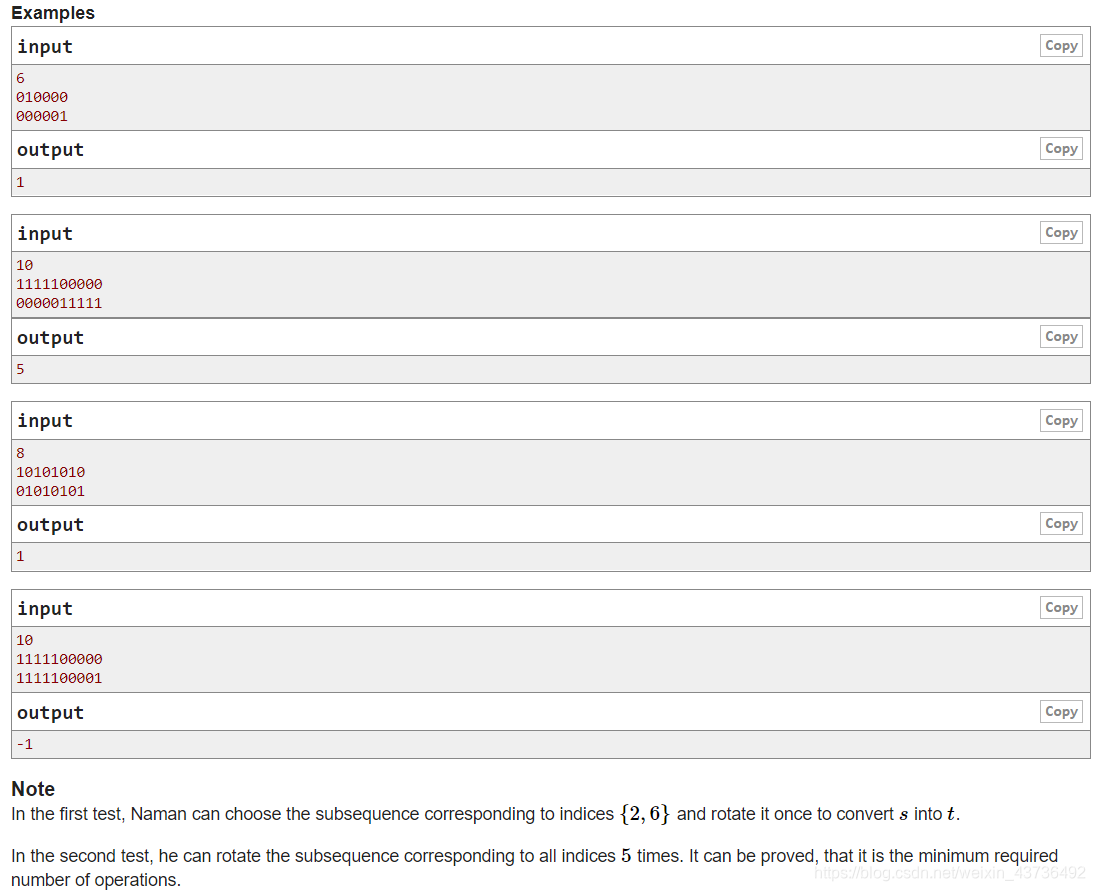
在这里插入图片描述

思路：

https://blog.youkuaiyun.com/qq_45458915/article/details/106909453

看的这位大佬的讲的非常清楚。
代码：

#include<iostream>
#include<string>
#include<algorithm>
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cstring>
#include<vector>
using namespace std;

const int maxn = 1e6 + 10;
char s[maxn],t[maxn];
void solved(){
    int n;cin>>n;
    scanf("%s%s",s + 1,t + 1);
    int cnt1 = 0,cnt2 = 0;
    for(int i = 1; i <= n; i++)if(s[i] == '1')cnt1++;
    for(int i = 1; i <= n; i++)if(t[i] == '1')cnt2++;
    if(cnt1 != cnt2){cout<<"-1"<<endl;return;}
    int ans = 0;
    int maxx = 0,minn = 0;
    for(int i = 1; i <= n; i++){
        ans += s[i] - t[i];
        maxx = max(ans,maxx);
        minn = min(ans,minn);
    }
    printf("%d\n",ans > 0 ? -1:maxx - minn);
}
int main(){
    solved();
    return 0;
}