“卓见杯”2020年河南省第二届CCPC大学生程序设计竞赛 I.太阳轰炸

最新推荐文章于 2023-03-02 16:45:21 发布

原创最新推荐文章于 2023-03-02 16:45:21 发布 · 1.5k 阅读

1 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

19 篇文章

订阅专栏

本文介绍了一种计算星灵太阳轰炸摧毁虚空碎片概率的方法。通过数学模型确定火焰飞弹命中目标的概率，并利用该概率计算摧毁目标的整体可能性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

背景：阿塔尼斯，达拉姆的大主教，在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰：亚顿之矛。作为艾尔星灵数千年来的智慧结晶，亚顿之矛除了搭载了以太阳能碎片为核心的兵工厂之外，还配备了诸如汇聚射线、太阳能射线枪等威力强大的支援武器。而在这些武器中，最负盛名、也最让敌人胆寒的就是太阳轰炸。
太阳轰炸是一件威力巨大的对星球武器。在太阳轰炸开火时，亚顿之矛将聚集太阳能核心中的太阳能量，向目标坐标发射成百上千枚火焰飞弹。虽然这些火焰飞弹精准度较差，但太阳轰炸的高攻击频率仍然可以让地面上的敌人无法躲避，化为灰烬。
在这一次的行动中，阿塔尼斯的目标是一枚臭名昭著的虚空碎片。在俯视视角下，虚空碎片的投影是一个半径为 R1 的圆，太阳轰炸的攻击散布范围是一个半径为 R2 的圆。这两个圆的圆心均为原点 (0,0)。太阳轰炸将射出 n 枚火焰飞弹，每一枚火焰飞弹等概率地落在攻击散布范围内每一个点上，所有火焰飞弹的落点相互独立。火焰飞弹的伤害范围是以落点为圆心，半径为 r 的圆。若火焰飞弹的伤害范围和虚空碎片的投影相交，则该枚火焰飞弹命中虚空碎片，造成 a 点伤害。若总伤害大于等于 h，则虚空碎片会被摧毁。
摧毁这枚虚空碎片对阿塔尼斯的战略部署非常重要，因此阿塔尼斯想要知道一次太阳轰炸能够摧毁这枚虚空碎片的概率。你需要输出答案对质数 109+7 取模的值。

输入

仅一行，包含六个整数 n, R1, R2, r, a, h (1≤n≤5×106, 1≤R1,R2,r≤108, 1≤a,h≤108)，含义见题目描述。

输出

一个整数，表示答案。

样例输入 Copy

3 2 4 1 1 1

样例输出 Copy

636962896

提示

答案对质数109+7 取模的定义：设 M=109+7，可以证明答案可表示为一个既约分数 p/q，其中 , 均为整数且 q 模 M 不余 0。输出满足 0≤x<M 且x⋅q≡p(mod M) 的整数 x。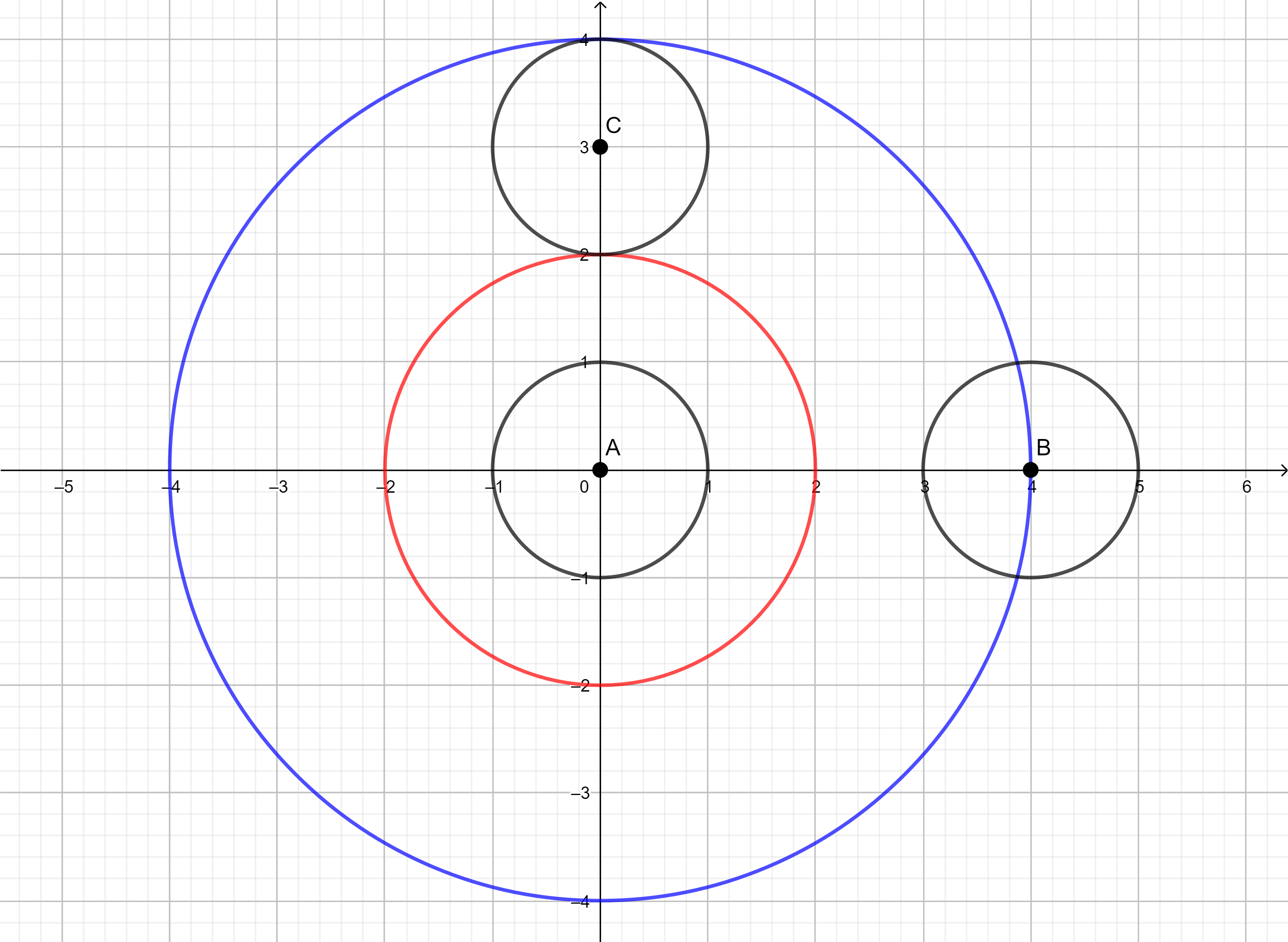
tle="" align="" />
上图对应了样例中 R1=2,R2=4,r=1 的情况。其中红色的圆是虚空碎片的投影，蓝色的圆是太阳轰炸的攻击范围。A,B,C 是三个可能的落点，其中 A,C 命中虚空碎片，而 B 没有命中虚空碎片。

思路：

R2这个圆是攻击范围，R1是目标，r是导弹的攻击半径，所以恰好不攻击到的范围就是导弹跟目标相切，这个时候距离就是R1 + r，只要在这个范围以内的

都可以对目标造成伤害，导弹击中目标的概率就是 $\frac{\left ( R_{1}+r \right )^{2}}{(R_{2})^{2}}$ ,但是概率不能超过1，所以跟1取min，枚举导弹击中的次数，算一下概率就可以了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
 
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 5e6 + 10;
 
ll fpow(ll a, int b, int mod) { ll res = 1; for (; b > 0; b >>= 1) { if (b & 1) res = res * a % mod; a = a * a % mod; } return res; }
int jc[N], inv[N];
int fz1[N], fz2[N];
int main()
{
#ifdef LOCAL
    freopen("E:/input.txt", "r", stdin);
#endif
    jc[0] = 1;
    for (int i = 1; i <= 5e6; i++)
        jc[i] = 1LL * jc[i - 1] * i % mod;
    inv[5000000] = fpow(jc[5000000], mod - 2, mod);
    for (int i = 5e6 - 1; i >= 0; i--)
        inv[i] = 1LL * inv[i + 1] * (i + 1) % mod;
    ll n, r1, r2, r, a, h;
    cin >> n >> r1 >> r2 >> r >> a >> h;
    ll fm = 1, x1 = r2 * r2 % mod, x2 = (r1 + r) * (r1 + r) % mod, x3 = (x1 - x2 + mod) % mod;
    fz1[0] = fz2[0] = 1;
    for (int i = 1; i <= n; i++)
    {
        fm = fm * x1 % mod;
        fz1[i] = 1LL * fz1[i - 1] * x2 % mod;
        fz2[i] = 1LL * fz2[i - 1] * x3 % mod;
    }
    ll res = 0;
    int flag = 0;
    for (int i = 1; i <= n; i++)
    {
        if (i * a >= h)
        {
            flag = 1;
            ll f = 1LL * jc[n] * inv[i] % mod * inv[n - i] % mod;
            res = (res + 1LL * f * fz1[i] % mod * fz2[n - i] % mod) % mod;
        }
    }
    if ((r1 + r) >= r2)
    {
        printf("%d\n", flag);
        exit(0);
    }
    cout << res * fpow(fm, mod - 2, mod) % mod << endl;
    return 0;
}