2019牛客暑期多校训练营（第二场）----E-MAZE

首先发出题目链接：
链接：https://ac.nowcoder.com/acm/contest/882/D
来源：牛客网
涉及：线段树，矩阵快速幂

点击这里回到2019牛客暑期多校训练营解题—目录贴

---

题目如下：



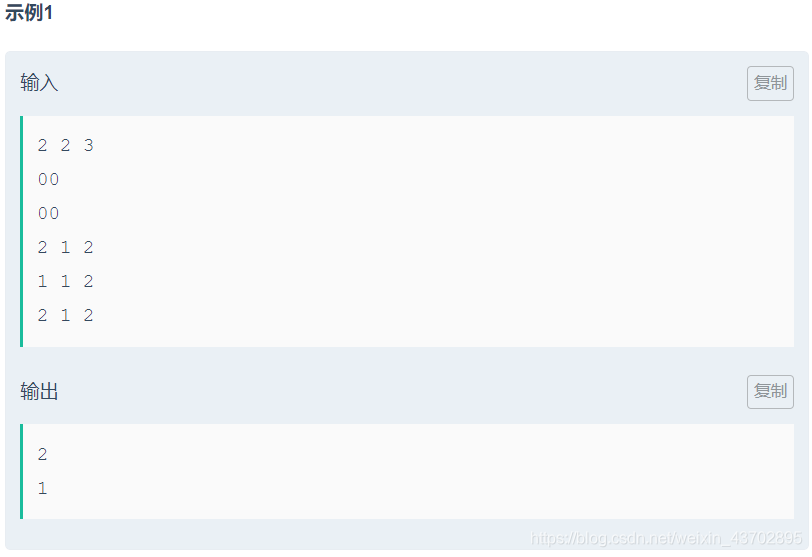
这是一个进阶版的走网格，但是现在是从上面往左右或者下方走，而且起点和终点是不固定，但起点和终点所在的行数是固定的，同时，还有一些地方是不能走的。

很明显，变了样子，还是变不了dp的方法。仍然是从dp的方向考虑问题。

---

我们主要考虑行与行之间的关系，很明显，下一行的某个位置子肯定是由上一行的一些位置走过有来的。

假设整个地图我们存在一个二维数组$map$中（这个$map$是数组的名字）。于是
$map[i][j]=0$说明此位置是可以通过的，否则不能通过。

我们假设$dp[i][j]$代表经过$map[i-1][j]$到达$map[i][j]$位置的路径数。

于是可以得到dp式
$$dp[i][j]=\{\begin{array}{ll}0& map[i-1][j]=1\\ {\sum }_{k=a}^{b}dp[i-1][k](a<j<b且{\sum }_{k=a}^{b}map[i-1][k]=0)& map[i-1][j]=0\end{array}$$

解释一下dp式是啥意思：
如图所示是第一行的map值

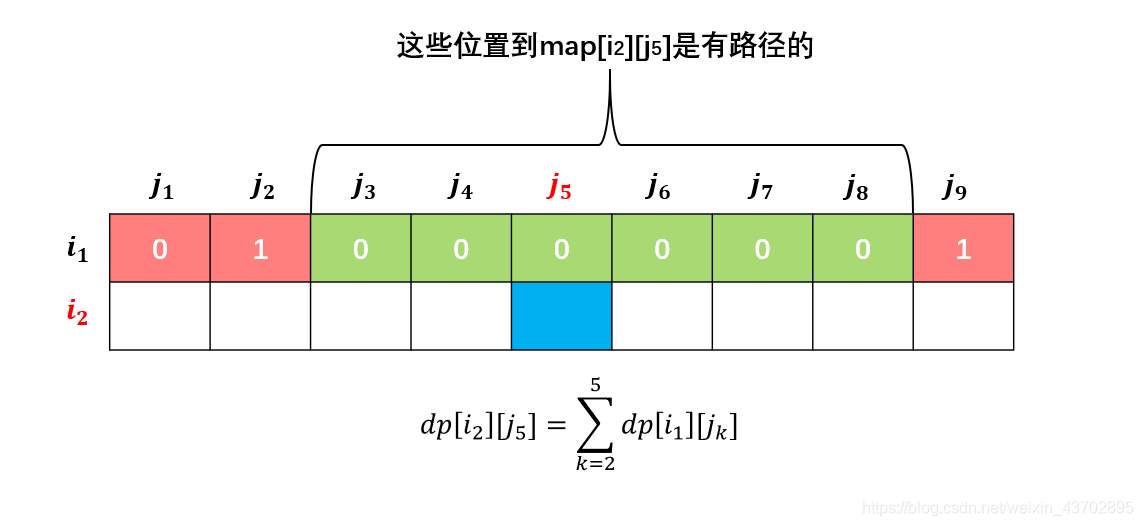
如图所示，先不管$map[i_2][j_5]$是不是1。

由于$map[i_1][j_2]$和$map[i_1][j_9]$都为1（无法通过），所以只有上图六个颜色为绿色的位置才能到达$map[j_2][j_5]$的位置（经过$map[i_1][j_5]$），故$dp[i_2][j_5]={\sum }_{k=2}^{5}dp[i_1][j_6]$

同理$dp[i_2][j_1]=dp[i_1][j_1]$

---

于是发现
$dp[i][1],dp[i][2],dp[i][3],...,dp[i][m]$可以由
$dp[i-1][1],dp[i-1][2],dp[i-1][3],...,dp[i-1][m]$来线性表示

涉及线性，且m比较小，可以用矩阵来做。每两行之间都会有dp值的转移矩阵。

而且从$dp[i]$到$dp[i+1]$的转移矩阵只与$map$有关
假设map第$i$行为

那么$dp[i]$到$dp[i+1]$的转移矩阵为
$$\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 1& 1\end{array}\right]$$
满足

$${\left[\begin{array}{c}dp[i+1][1]\\ dp[i+1][2]\\ dp[i+1][3]\\ dp[i+1][4]\\ dp[i+1][5]\\ dp[i+1][6]\\ dp[i+1][7]\\ dp[i+1][8]\end{array}\right]}^T={\left[\begin{array}{c}dp[i][1]\\ dp[i][2]\\ dp[i][3]\\ dp[i][4]\\ dp[i][5]\\ dp[i][6]\\ dp[i][7]\\ dp[i][8]\end{array}\right]}^T\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 1& 1\end{array}\right]$$

---

如何得到map中某一行的转移矩阵：

转移矩阵中第i列控制着dp第i列的值。

对于一个dp[i][j]，我们只要看map[i-1]的哪些地方可以到达map[i-1][j]。可以分别从map[i-1][j]向左和向右遍历。

求第x行的转移矩阵，参考代码：

for(int i=1;i<=m;i++){
	if(map[x][i]==1)	continue;//如果map[x][i]本身就是1，那么一定不能到达下一行。
	else tree[k].mul.trmap[i][i]=1;//否则可以，然后向左和向右遍历。
	for(int j=i+1;j<=m;j++){
		if(map[x][j]==0)	tree[k].mul.trmap[j][i]=1;
		else break;
	}
	for(int j=i-1;j>0;j--){
		if(map[x][j]==0)	tree[k].mul.trmap[j][i]=1;
		else break;
	}
}

---

每一行的转移矩阵求出来，假设第i行的转移矩阵为$M_i$，dp[1]的所有值我们也知道（从map[1][a]出发那么dp[1][a]=1，其他dp[1]全为0）

假设终点为map[n][b]，答案即为dp[n+1][b]（注意dp[n+1][b]为经过map[n][b]到达map[n+1][b]的路径数），而不是dp[n][b]。

于是
$${\left[\begin{array}{c}dp[n+1][1]\\ dp[n+1][2]\\ dp[n+1][3]\\ dp[n+1][4]\\ dp[n+1][5]\\ dp[n+1][6]\\ dp[n+1][7]\\ dp[n+1][8]\end{array}\right]}^T={\left[\begin{array}{c}dp[1][1]\\ dp[1][2]\\ dp[1][3]\\ dp[1][4]\\ dp[1][5]\\ dp[1][6]\\ dp[1][7]\\ dp[1][8]\end{array}\right]}^T{M}_1{M}_2...M_n$$

同时发现从map[1][a]到map[n][b]的路径数其实就是所有转移矩阵相乘后（假设为M）M[a][b]的值（初始dp[1]向量中只有第a个值为1，相当于选择M矩阵的第a行，到达map[n][b]就是选取第b列）

---

每次修改map[x][j]的状态，相当于修改转移矩阵$M_x$（第x行）

可以用线段树动态维护矩阵的乘积。注意取模和矩阵乘法

矩阵乘法（运算符重载）

struct array{
	ll trmap[maxm][maxm];
	array operator*(array &ar){
		array x;
		memset(x.trmap,0,sizeof(x.trmap));
		int i,j,k;
		for(i=1;i<=m;i++)
			for(j=1;j<=m;j++)
				for(k=1;k<=m;k++)
					x.trmap[i][j]=(x.trmap[i][j]+this->trmap[i][k]*ar.trmap[k][j])%mod;
		return x;
	}
}; 

---

代码如下：

#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
//三个最值
const int maxn=50005;
const int maxm=12;
const int mod=1e9+7;
//n，m，q为题目所给变量，v用来创建线段树的叶子节点（表示现在该创建第v个转移矩阵叶子节点）
int n,m,q,v=1; 
int map[maxn][maxm];//地图，只存0和1
struct array{//矩阵结构体
	ll trmap[maxm][maxm];
	array operator*(array &ar){//运算符重载，方便矩阵相乘
		array x;
		memset(x.trmap,0,sizeof(x.trmap));
		int i,j,k;
		for(i=1;i<=m;i++)
			for(j=1;j<=m;j++)
				for(k=1;k<=m;k++)
					x.trmap[i][j]=(x.trmap[i][j]+this->trmap[i][k]*ar.trmap[k][j])%mod;
		return x;
	}
}; 
struct op{//线段树节点
	int l,r;
	array mul;
};
op tree[4*maxn];
void build(int l,int r,int k){//创建线段树
	tree[k].l=l;
	tree[k].r=r;
	if(l==r){//l与r相等时就创建叶子节点
		for(int i=1;i<=m;i++){
			if(map[v][i]==1)	continue;//如果map[x][i]本身就是1，那么一定不能到达下一行。
			else tree[k].mul.trmap[i][i]=1;//否则可以，然后向左和向右遍历。
			for(int j=i+1;j<=m;j++){
				if(map[v][j]==0)	tree[k].mul.trmap[j][i]=1;
				else break;
			}
			for(int j=i-1;j>0;j--){
				if(map[v][j]==0)	tree[k].mul.trmap[j][i]=1;
				else break;
			}
		}
		v++;//v++表示下一个该创建第v个转移矩阵叶子节点
		return;
	}
	int pos=(l+r)/2;
	build(l,pos,2*k);
	build(pos+1,r,2*k+1);
	tree[k].mul=tree[2*k].mul*tree[2*k+1].mul;//状态合并
	return;
}
void add(int x,int k){//单点修改
	if(tree[k].l==tree[k].r){
		memset(tree[k].mul.trmap,0,sizeof(tree[k].mul.trmap));//先初始化为0
		for(int i=1;i<=m;i++){//根据新的map值重新创建当前转移矩阵叶子节点
			if(map[x][i]==1)	continue;
			else tree[k].mul.trmap[i][i]=1;
			for(int j=i+1;j<=m;j++){
				if(map[x][j]==0)	tree[k].mul.trmap[j][i]=1;
				else break;
			}
			for(int j=i-1;j>0;j--){
				if(map[x][j]==0)	tree[k].mul.trmap[j][i]=1;
				else break;
			}
		}
		return;
	} 
	int pos=(tree[k].l+tree[k].r)/2;
	if(x<=pos)	add(x,2*k);
	else	add(x,2*k+1);
	tree[k].mul=tree[2*k].mul*tree[2*k+1].mul;//状态合并
	return;
}
int main(){
	scanf("%d%d%d",&n,&m,&q);
	int i,j;
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)	scanf("%1d",&map[i][j]);//注意一个个输入，所以用%1d
	build(1,n,1);//创建线段树
	while(q--){
		int p,a,b;
		scanf("%d%d%d",&p,&a,&b);
		if(p==1)	map[a][b]^=1,add(a,1);//先修改map值，再根据新map值修改转移矩阵叶子节点
		else	printf("%lld\n",tree[1].mul.trmap[a][b]);//tree[1]存的是全部转移矩阵的乘积
	}	
	return 0;
}