首先发出题目链接:
链接:https://ac.nowcoder.com/acm/contest/881/F
来源:牛客网
涉及:概率期望
点击这里回到2019牛客暑期多校训练营解题—目录贴
题目如下:

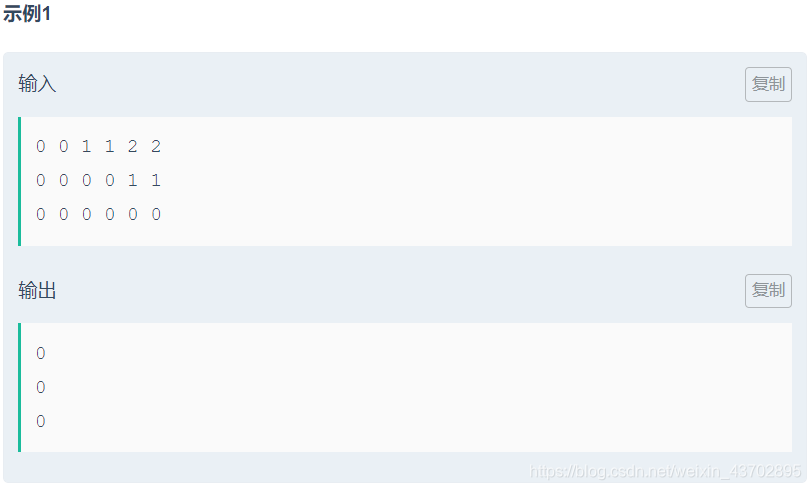
题目好水啊
首先将
△
A
B
C
\triangle_{ABC}
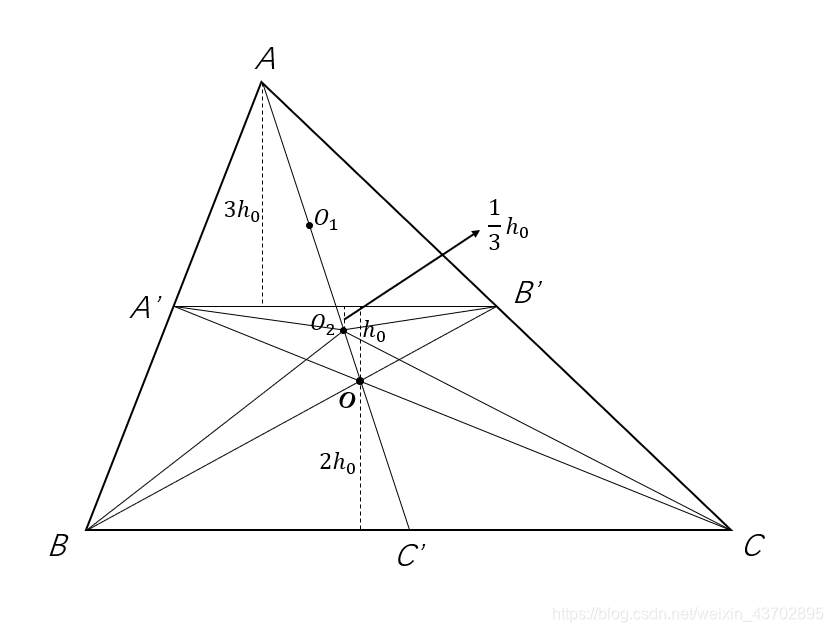
△ABC这样分解,如图所示
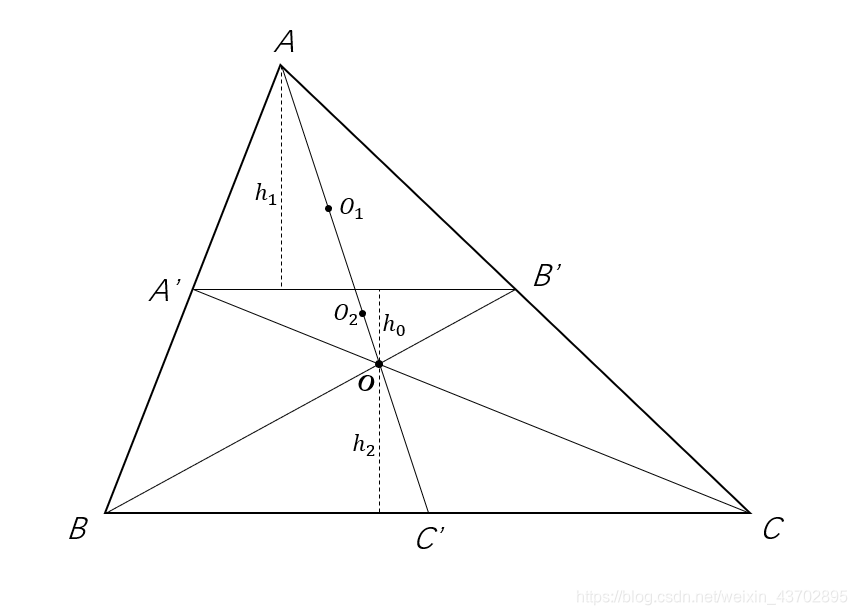
解释一波:
A ′ , B ′ , C ′ A',B',C' A′,B′,C′分别为 A B , A C , B C AB,AC,BC AB,AC,BC的中点, O O O为 △ A B C \triangle_{ABC} △ABC的重心
h 1 , h 0 , h 2 h_1,h_0,h_2 h1,h0,h2分别为 △ A A ′ B ′ , △ A ′ B ′ O , △ O B C \triangle_{AA'B'},\triangle_{A'B'O},\triangle_{OBC} △AA′B′,△A′B′O,△OBC的高,且 h 0 + h 1 + h 2 h_0+h_1+h_2 h0+h1+h2为 △ A B C \triangle_{ABC} △ABC的高
O 1 , O 2 O_1,O_2 O1,O2分别为 △ A A ′ B ′ , △ A ′ B ′ O \triangle_{AA'B'},\triangle_{A'B'O} △AA′B′,△A′B′O的重心
首先确定一点:若P落在四边形 A A ′ O B ′ AA'OB' AA′OB′内,那么 m a x { S A P B , S B P C , S C P A } = S B P C max\left\{S_{APB},S_{BPC},S_{CPA}\right\}=S_{BPC} max{SAPB,SBPC,SCPA}=SBPC
然后再来判断
h
0
,
h
1
,
h
2
h_0,h_1,h_2
h0,h1,h2之间的关系:
由于
△
A
′
B
′
O
\triangle_{A'B'O}
△A′B′O与
△
B
C
O
\triangle_{BCO}
△BCO相似,且
2
∣
O
A
′
∣
=
∣
O
C
∣
2|OA'|=|OC|
2∣OA′∣=∣OC∣,故
h
2
=
2
h
0
h_2=2h_0
h2=2h0;
由于
h
1
=
h
0
+
h
2
h_1=h_0+h_2
h1=h0+h2,故
h
1
=
3
h
0
h_1=3h_0
h1=3h0
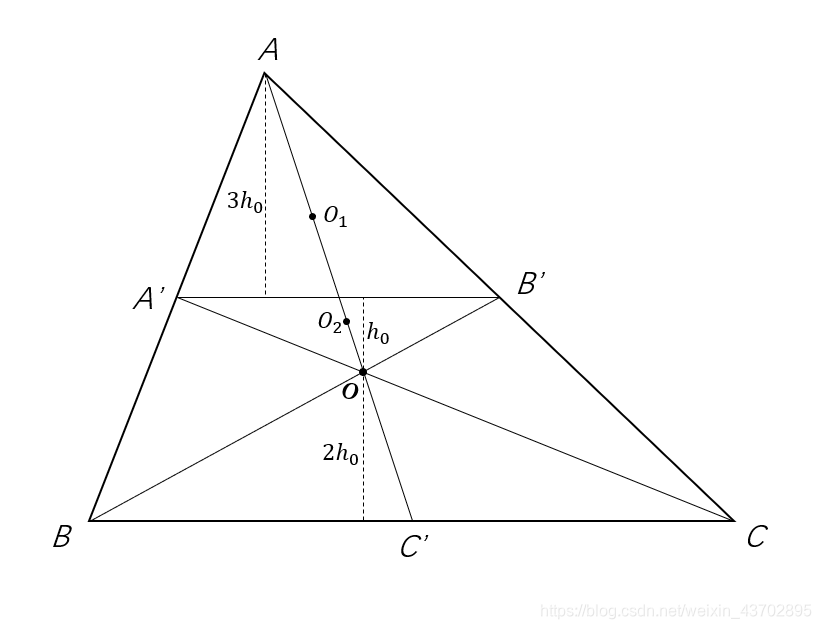
1.考虑P点落在 △ A A ′ B ′ \triangle_{AA'B'} △AA′B′内
如图所示,P点落在
△
A
A
′
B
′
\triangle_{AA'B'}
△AA′B′中时,
S
P
B
C
S_{PBC}
SPBC的期望刚好是
S
O
1
B
C
S_{O_1BC}
SO1BC
此时
E
S
P
B
C
=
S
O
1
B
C
=
1
2
(
h
0
+
h
0
+
2
h
0
)
∣
B
C
∣
=
2
h
0
∣
B
C
∣
E_{S_{PBC}}=S_{O_1BC}=\frac {1}{2}(h_0+h_0+2h_0)|BC|=2h_0|BC|
ESPBC=SO1BC=21(h0+h0+2h0)∣BC∣=2h0∣BC∣
2.考虑P点落在
△
O
A
′
B
′
\triangle_{OA'B'}
△OA′B′内
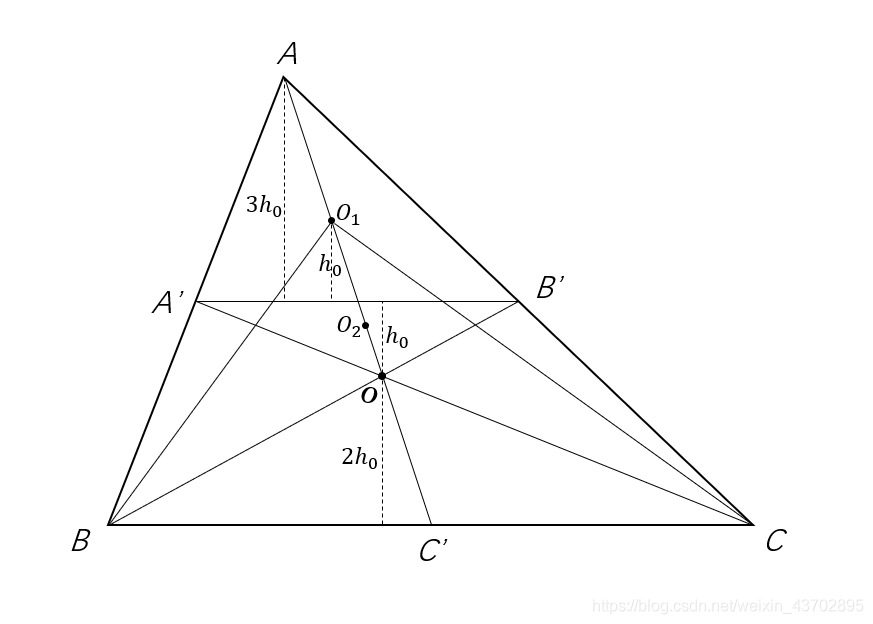
如图所示,P点落在
△
O
A
′
B
′
\triangle_{OA'B'}
△OA′B′中时,
S
P
B
C
S_{PBC}
SPBC的期望刚好是
S
O
2
B
C
S_{O_2BC}
SO2BC
由于
△
O
2
A
′
B
′
\triangle_{O_2A'B'}
△O2A′B′的高为
1
3
h
0
\frac 1{3}h_0
31h0,所以
△
O
2
B
C
\triangle_{O_2BC}
△O2BC的高为
(
h
0
−
1
3
h
0
+
2
h
0
)
=
8
3
h
0
(h_0-\frac 1{3}h_0+2h_0)=\frac 8{3}h_0
(h0−31h0+2h0)=38h0
此时 E S P B C = S O 2 B C = 1 2 ∗ 8 3 h 0 ∣ B C ∣ = 4 3 h 0 ∣ B C ∣ E_{S_{PBC}}=S_{O_2BC}=\frac {1}{2}*\frac 8{3}h_0|BC|=\frac 4 {3}h_0|BC| ESPBC=SO2BC=21∗38h0∣BC∣=34h0∣BC∣
由于 3 S A ′ B ′ O = S A A ′ B ′ 3S_{A'B'O}=S_{AA'B'} 3SA′B′O=SAA′B′,所以P点落在 △ A A ′ B ′ \triangle_{AA'B'} △AA′B′的概率为 3 4 \frac 3 {4} 43,落在 △ O A ′ B ′ \triangle_{OA'B'} △OA′B′的概率为 1 3 \frac 1{3} 31
所以P点落在四边形
A
A
′
O
B
′
AA'OB'
AA′OB′的期望
E
A
A
′
O
B
′
E_{AA'OB'}
EAA′OB′
E
A
A
′
O
B
′
=
1
4
S
O
2
B
C
+
3
4
S
O
1
B
C
=
11
6
h
0
∣
B
C
∣
E_{AA'OB'}=\frac 1{4}S_{O_2BC}+\frac 3{4}S_{O_1BC}=\frac {11}{6}h_0|BC|
EAA′OB′=41SO2BC+43SO1BC=611h0∣BC∣
而P点落在四边形
A
A
′
O
B
′
,
A
′
O
C
′
B
,
B
′
O
C
′
C
AA'OB',A'OC'B,B'OC'C
AA′OB′,A′OC′B,B′OC′C的概率是相同的。
所以
E
=
E
A
A
′
O
B
′
=
11
6
h
0
∣
B
C
∣
=
11
18
S
A
B
C
E=E_{AA'OB'}=\frac {11}{6}h_0|BC|=\frac {11}{18}S_{ABC}
E=EAA′OB′=611h0∣BC∣=1811SABC
而
36
E
=
22
S
A
B
C
36E=22S_{ABC}
36E=22SABC
注意,答案是long long类型,在算期望的过程中也要注意类型转换!!
已知三点坐标为
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
(
x
3
,
y
3
)
(x_1,y_1),(x_2,y_2),(x_3,y_3)
(x1,y1),(x2,y2),(x3,y3),则三角形面积
S
=
∣
(
x
2
−
x
1
)
∗
(
y
3
−
y
1
)
−
(
y
2
−
y
1
)
∗
(
x
3
−
x
1
)
∣
S=|(x_2-x_1)*(y_3-y_1)-(y_2-y_1)*(x_3-x_1)|
S=∣(x2−x1)∗(y3−y1)−(y2−y1)∗(x3−x1)∣
注意 ( x 2 − x 1 ) ∗ ( y 3 − y 1 ) (x_2-x_1)*(y_3-y_1) (x2−x1)∗(y3−y1)和 ( y 2 − y 1 ) ∗ ( x 3 − x 1 ) (y_2-y_1)*(x_3-x_1) (y2−y1)∗(x3−x1)都是long long类型
代码如下:
#include <iostream>
#include <cmath>
using namespace std;
typedef long long ll;
int main(){
int x1,x2,x3;
int y1,y2,y3;
while(~scanf("%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3)){
ll ans=(ll)(x2-x1)*(y3-y1)-(ll)(y2-y1)*(x3-x1);//面积与三点坐标的公式求面积
printf("%lld\n",(ll)abs(ans)*11);//答案为22倍三角形面积
}
return 0;
}




 本文详细解析了牛客网2019暑期多校训练营中的一道概率题目,通过几何分解和重心概念,推导出点P落在△ABC内时,SAPB、SBPC、SCPA的最大值期望。文章提供了完整的数学证明和代码实现。
本文详细解析了牛客网2019暑期多校训练营中的一道概率题目,通过几何分解和重心概念,推导出点P落在△ABC内时,SAPB、SBPC、SCPA的最大值期望。文章提供了完整的数学证明和代码实现。
















 338
338

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








