Fibsieve`s Fantabulous Birthday(数学类-基础数学)

题面

Fibsieve had a fantabulous (yes, it’s an actual word) birthday party this year. He had so many gifts that he was actually thinking of not having a party next year.
Among these gifts there was an N x N glass chessboard that had a light in each of its cells. When the board was turned on a distinct cell would light up every second, and then go dark.
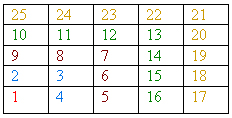
The cells would light up in the sequence shown in the diagram. Each cell is marked with the second in which it would light up.
(The numbers in the grids stand for the time when the corresponding cell lights up)
In the first second the light at cell (1, 1) would be on. And in the 5th second the cell (3, 1) would be on. Now, Fibsieve is trying to predict which cell will light up at a certain time (given in seconds). Assume that N is large enough.

Input

Input starts with an integer T (≤ 200), denoting the number of test cases.
Each case will contain an integer S (1 ≤ S ≤ 1015) which stands for the time.

Output

For each case you have to print the case number and two numbers (x, y), the column and the row number.

Sample Input

     3 
     8 
     20 
     25

Sample Output

     Case 1: 2 3 
     Case 2: 5 4 
     Case 3: 1 5

这个题的大体意思是给你一个数字，让你计算出他的坐标。
表格下边为x轴，表格左边为y轴，

例如给的样例8
1的坐标为 1 1
8的坐标为 2 3
11的坐标为 2 4

先观察给的表格，首先你会发现它的每一层的数量都是一个等差数列 1 3 5 7 9 11… 这个规律其实没大有用处，
观察x=1的这一列 1 9 25 都是奇数的平方而且开方后正是这个数的列数。
观察y=1的这一行，1 4 16都是偶数的平方，而且开方后正是这个数的行数。
观察对角线的数，1 3 7 13 21… 设列数为a 每列的对角线数都等于a*(a-1)+1

代码逻辑

输入一个数字n
对它开方（取整） a 比如8 开方后为2
如果开方的数字的平方等于n，说明这个数字在x=1这一列或者y=1这一行，判断只需要看他开方是奇数还是偶数就行了。
如果开方的数字的平方不等于n，计算对角线的数字，a*(a+1)+1 刚才说的是a*(a-1）+1 不矛盾 ，你看开方后要取整 按照取完后的数计算是计算的它前一层的对角线的数 所以前面的式子中的a要变成a+1，层数顺序的问题很好解决只需要判断a的奇偶性，如果为奇数，计算的是他a+1层 ，顺序跟第四层大小顺序一致，如果是偶数，也是计算的它a+1层，顺序跟第三层的大小顺序一样。

代码

#include<iostream>
#include<cmath>
typedef long long ll;
using namespace std;
int main()
{
 	int t,k=1;
	 cin>>t;
 	while(t--)
 { 
 	 ll n;
 	 cin>>n;
  	cout<<"Case "<<k++<<": ";
	  ll a=sqrt(n);
	  if(a*a==n)
		  {
		   if(a&1)
		   cout<<"1"<<" "<<a<<endl;
		   else
		   cout<<a<<" "<<"1"<<endl;
		   continue;
		   } 
		   if(a&1)
		   {
			    ll b=a*(a+1)+1;
			    if(n<b)
			   	  cout<<a+1-(b-n)<<" "<<a+1;
			    else
			   	  cout<<a+1<<" "<<a+1-(n-b);
			   }
			   else
		   {
		    	ll b=a*(a+1)+1;
		   	 if(n>b)
		   	  cout<<a+1-(n-b)<<" "<<a+1;
		    else
		  	   cout<<a+1<<" "<<a+1-(b-n);
		   }
		   cout<<endl;
 }
	 return 0;
 } 
	```