最长回文 HDU - 3068 （Manacher）

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度. 
回文就是正反读都是一样的字符串,如aba, abba等

Input

输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S 
两组case之间由空行隔开(该空行不用处理) 
字符串长度len <= 110000

Output

每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度. 

Sample Input

aaaa

abab

Sample Output

4
3

题意如题目

解题方法：Manacher算法

这道题要在给定字符串中找到最长的回文串，一般的暴力方法都可以实现，不过由于数据范围，也就意味着我们无法在时间复杂度为O(n^2)或更高的算法实现，只能以O(n)的复杂度算法实现

这里介绍一种算法：Manacher算法

算法十分巧妙，首先将字符串中首尾及各字母之间添加一个从未在字符串中出现的字符（这里以“#”为例）

比如aaaa，我们可以改写成#a#a#a#a#，不过还要在首尾添加字符，这样在后续的算法中就不必判断边界。

接下来，我们用一个数组a[n]，来存储以i为中心的回文子串的半径，即

snew[] = # a # a # a # a # （为方便观察，这里的字符之间添加了一个空格）

对应半径分别为

# a # a # a # a #

1 2 3 4 5 4 3 2 1（半径长度算自身）

则不难看出，a[i] - 1分别代表以i为中点的回文串的长度，则最长回文串长度为max(a[i] - 1)

那么，我们应如何求a[i]呢？

这基于动态规划的原理

定义两个辅助变量maxlen和imid，分别表示当前最长回文串的右边界和最长回文串的中点

援引其他博主画的结构图（id == imid， mx == maxlen）

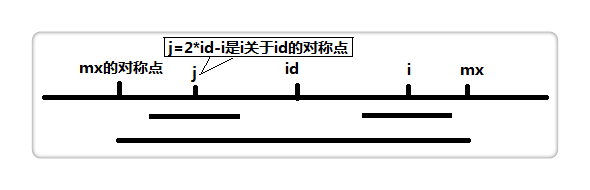
当 mx - i > a[j] 的时候，以snew[j]为中心的回文子串包含在以snew[id]为中心的回文子串中，由于 i 和 j 对称，以snew[i]为中心的回文子串必然包含在以snew[id]为中心的回文子串中，所以必有 a[i] = a[j]；

那么当 a[j] >= mx - i 的时候

此时，以snew[j]为中心的回文子串不一定完全是包含于snew[id]为中心的回文子串里，画绿色框框的部分仍旧对称，也依旧相同，但是超出mx的部分就需要一点一点比对了

对于 mx <= i 的情况，无法对 a[i]做更多的假设，只能a[i] = 1，然后再去匹配了。

这道题对于没有什么动态规划基础的我看着很是头疼，不过在参阅了很多博客之后，我对此也是有了一定程度的理解。

代码：

#include <iostream>  
#include <cstring>
#include <algorithm>  

using namespace std;

char s[200020];
char s_new[200020];
int p[200020];

int Init()
{
    int length = strlen(s);
    s_new[0] = '%';
    s_new[1] = '#';
    int j = 2;
    for(int i = 0; i < length; i++){
    	s_new[j++] = s[i];
    	s_new[j++] = '#';
    }
    s_new[j] = '\0';
    return j;
}

int Manacher()
{
    int len = Init();  
    int max_len = -1;  
    int id = 0;
    int mx = 0;
    for(int i = 1; i < len; i++){
    	if(i < mx)
    		p[i] = min(p[2 * id - i], mx - i);
    	else
    		p[i] = 1;
    	while(s_new[i - p[i]] == s_new[i + p[i]])
    		p[i]++;	
    	if(mx < i + p[i]){
    		id = i;
    		mx = i + p[i];
    	}
    	max_len = max(max_len, p[i] - 1);
    }

    return max_len;
}

int main()
{
    while (scanf("%s", s) != EOF)
    {  
        printf("%d\n", Manacher());
    }
    return 0;
}