四. 逻辑回归
1. 分类问题
在分类问题中,要预测的变量 𝑦 是离散的值,尝试预测的是结果是否属于某一个类(例如正确或错误)。
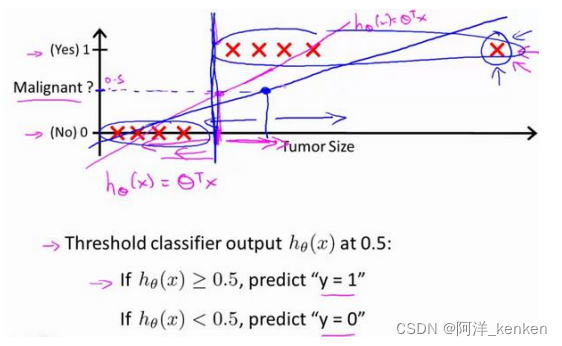
线性回归算法
线性回归算法,因为其预测的值可以超越[0,1]的范围,不适用于分类问题,引入逻辑回归 (Logistic Regression)算法。
2. 假说表示
我们希望想出一个满足某个性质的假设函数,这个性质是它的预测值要在 0 和 1 之间。
逻辑回归模型的假设是:其中: 𝑋 代表特征向量,𝑔 代表逻辑函数(logistic function)是一个常用的逻辑函数为 S 形函数(Sigmoid function),公式为:
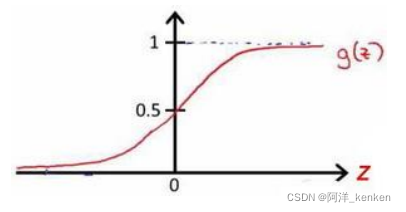
sigmoid function
ℎ𝜃(𝑥)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity)即
3. 判定边界(决策界限)
(1)在逻辑回归中,我们预测:
当ℎ𝜃 (𝑥) >= 0.5时,预测 𝑦 = 1。
当ℎ𝜃 (𝑥) < 0.5时,预测 𝑦 = 0 。
(2)在sigmoid函数中:z>=0,g(z)>=0.5;z<0,g(z)<0.5
(3)<0,y=0;
>=0,y=1
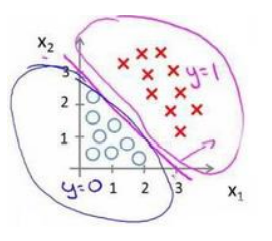
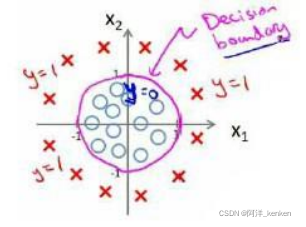
决策边界
为决策边界(decision boundar)
4. 代价函数
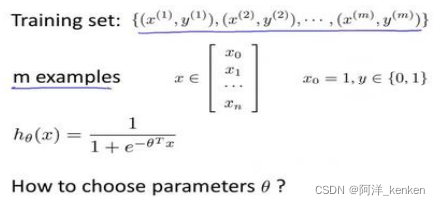
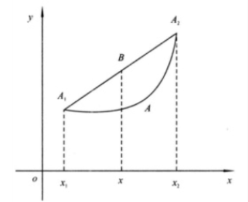
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。若对逻辑回归模型沿用这个定义,由于sigmoid函数的影响,得到的代价函数将是一个非凸函数(non-convexfunction)。代价函数有许多局部最小值,影响梯度下降算法寻找全局最小值。
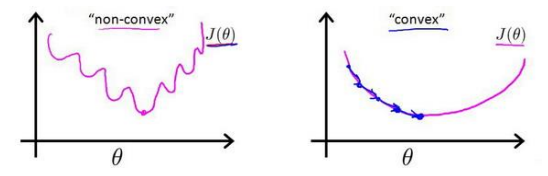
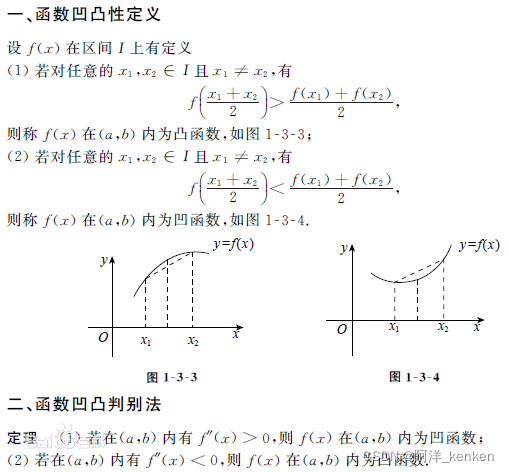
凹凸性:
同济高等数学定义*同济大学出版的高数中关于函数凹凸性的定义与国际上的相反
凸函数 convex function
国际上convex function斜率增加(单调不减),二阶导为正。
凸函数性质:局部最小值是全局最小值(得到的解一定是全局最优解)
(1)需定义一个为凸函数的代价函数:(极大似然思想)
逻辑回归的代价函数为:
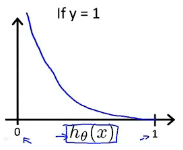
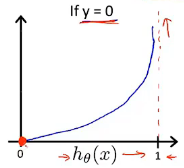
(2)代价函数特点:当实际 y=1 且 也为1时,误差为0;当 y=1 但
不为1时,误差随
变小而增大(差的越多,代价增大的越快)。y=0 时同理。
(3)简化代价函数:
写成一个式子,方便梯度下降
5. 梯度下降
goal:找尽量让J(θ)取得最小值的参数θ
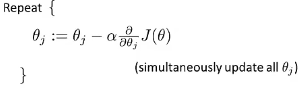
梯度下降模板
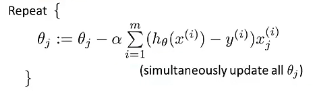
求导并带入
推导后发现与逻辑回归与线性回归得到的梯度下降公式相同,但是 两者不同,具体带入时有区别。
同时更新:for循环、向量化
6. 高级优化
共轭梯度法、BFGS (变尺度法) 、L-BFGS (限制变尺度法)
优点:无需人工选择参数α(智能内部循环:线性搜索)、运算速度比梯度下降更快
缺点:更加复杂
7. 多类别分类:一对多
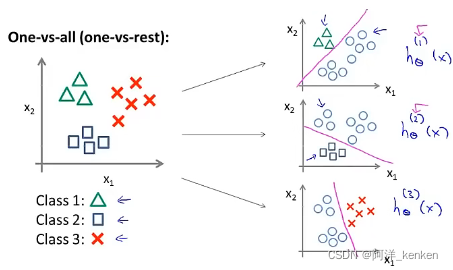
原理
拟合出三个分类器,
在预测时,将所有的分类机运行一遍,对每一个输入变量都选择最高可能性的输出变量。
五. 正则化
1. 过拟合
e.g. 线性回归
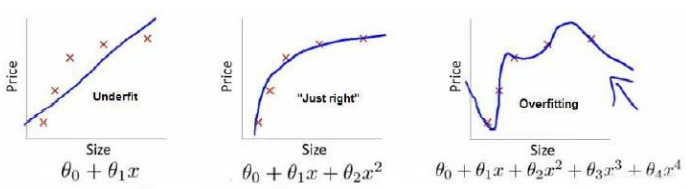
欠拟合、合适、过拟合
e.g. 逻辑回归
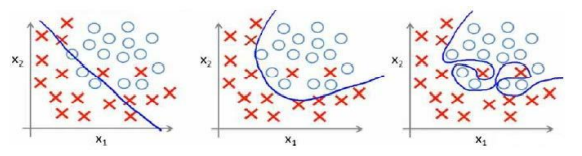
欠拟合、合适、过拟合
(1)欠拟合、高偏差:
说明没有很好的拟合训练数据
解决办法:增加特征,如增加多项式
(2)过拟合,高方差:
拟合训练数据过于完美,J(θ) ≈ 0,导致模型的泛化能力很差,对于新样本不能准确预测
解决办法:减少特征个数:人工/模型选择算法(PCA)
正则化:保留所有特征,减小参数维度(magnitude)
2. 代价函数
高次项导致的过拟合的产生,让这些高次项的系数接近于0的话,就能很好的拟合。
正则化基本方法:加入惩罚项,在一定程度上减小某些参数𝜃的值。
代价函数:
(1)线性回归:
λ:正则化参数(Regularization Parameter)
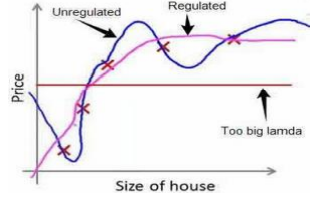
正则化前后对比
如果正则化参数 λ 过大,所有的 𝜃 的值(不包括𝜃0)都会在一定程度上减小,可能会欠拟合,应选取合理的 λ 值。
(2)逻辑回归:
3. 线性回归的正则化
(1)梯度下降法
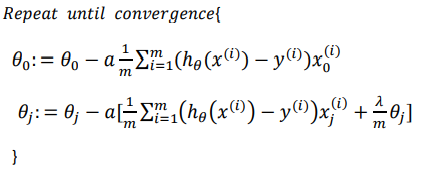
(2)正规方程法
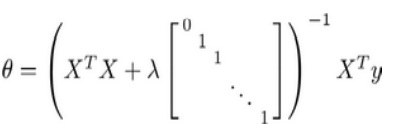
矩阵尺寸为(n+1)*(n+1)
正规方程法需满足矩阵可逆,加入正则化项后矩阵一定可逆,无需考虑不可逆的情况。
4. 逻辑回归的正则化
(1)梯度下降法

与线性回归的区别是具体带入的 不同。
(2)高级优化算法
Octave 中,我们依旧可以用 fminuc 函数来求解代价函数最小化的参数,值得注意的是参数𝜃0的更新规则与其他情况不同。
 逻辑回归详解:分类、决策边界与正则化
逻辑回归详解:分类、决策边界与正则化





















 9443
9443

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








