目录

非线性数据结构深度解析:从层次模型到网络拓扑
非线性表:与线性表对立,在非线性表之中,数据之间并不是简单的前后关系。非线性表结构:二叉树、堆、图等。
非线性表的本质特征
非线性表是数据元素之间存在一对多或多对多关系的逻辑结构,其核心特征为:
- 非顺序性:数据元素不存在唯一的前驱和后继关系(区别于线性表)。
- 层次或网状特性:数据组织呈现树形分支或图状网络结构。
- 递归定义:多数非线性结构可递归分解为子结构(如树的子树、图的连通分量)。
树形结构:层次化数据的典型代表
树(Tree)
树[Tree]是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
- 有且仅有一个特定的称为根[Root]的结点;
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、…、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
- 根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
- 子树的个数没有限制,但它们一定是互不相交的。
如图,是一棵普通树
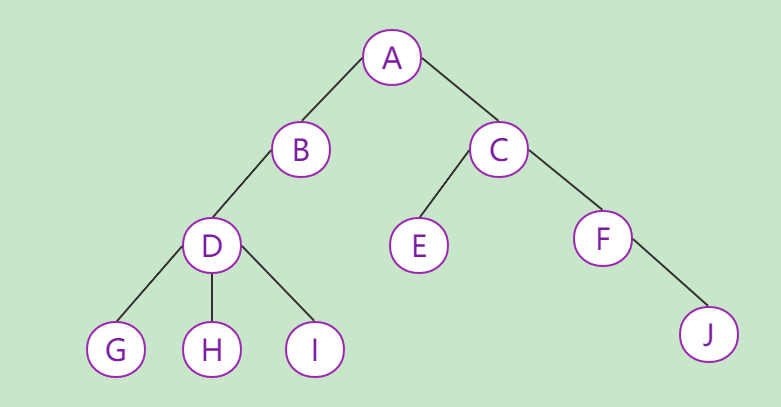
度数:结点拥有的子树数目称为结点的 度 。
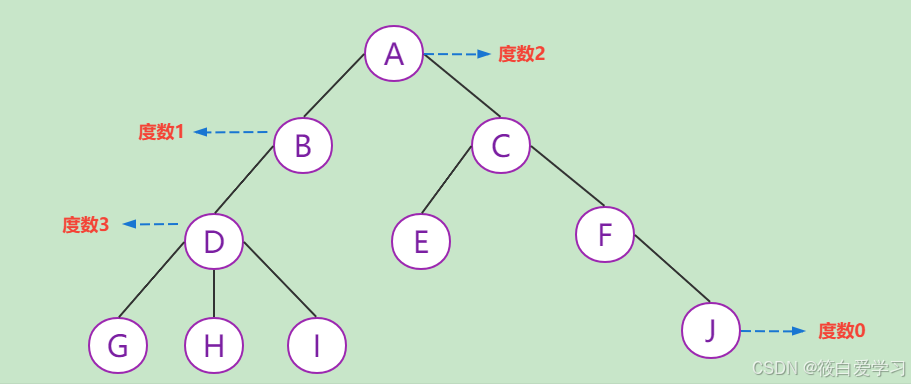
节点关系:
- 孩子结点
- 双亲结点
- 兄弟结点
节点层次:
从根开始定义起,根为第一层,根的孩子为第二层,以此类推。
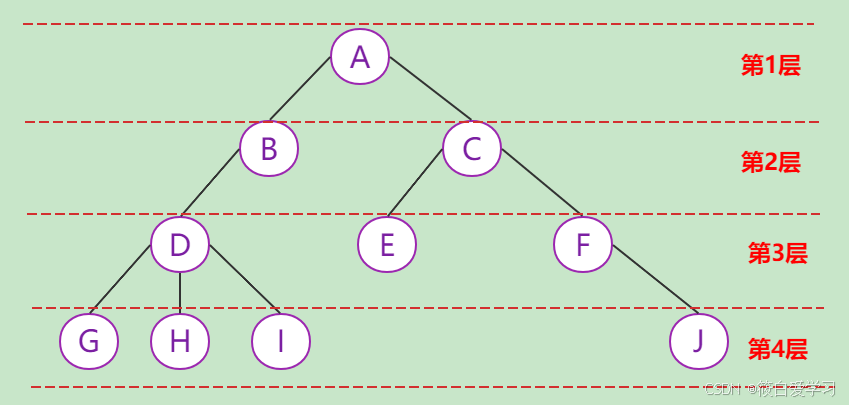
树的深度:
树中结点的最大层次,如上图深度为4
二叉树
概念介绍
每个子节点只有两个节点的树,每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒。
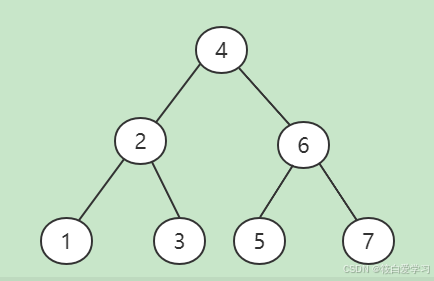
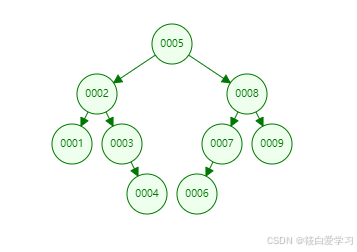
二叉查找树
也称为有序二叉查找树,满足二叉查找树的一般性质,是指一棵空树具有如下性质:
- 任意节点左子树不为空,则左子树的值均小于根节点的值
- 任意节点右子树不为空,则右子树的值均大于于根节点的值
- 任意节点的左右子树也分别是二叉查找树
- 没有键值相等的节点
二叉树又分为:
-
完美二叉树
-
完全二叉树
-
完满二叉树
完美二叉树
又称为 满二叉树 ,除了叶子节点之外的每一个节点都有两个孩子节点,每层都被完全填充
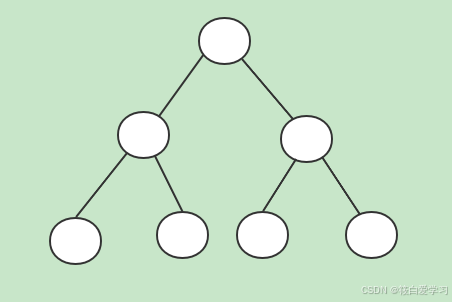
完全二叉树
除了最后一层之外的其他每一层都被完全填充,并且所有的节点都保持向左对齐
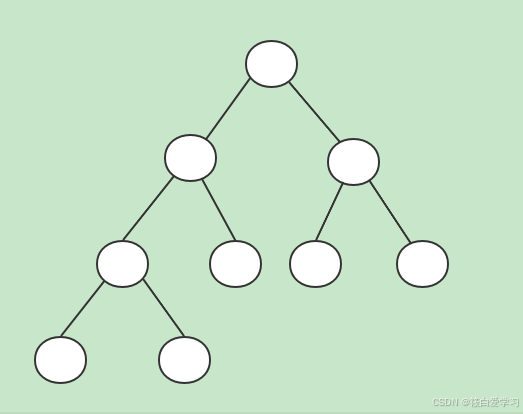
完满二叉树
除了叶子节点之外的每一个节点都有两个孩子节点。
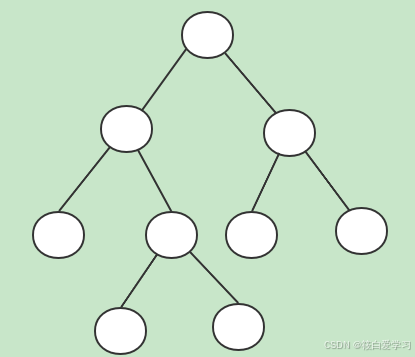
遍历操作
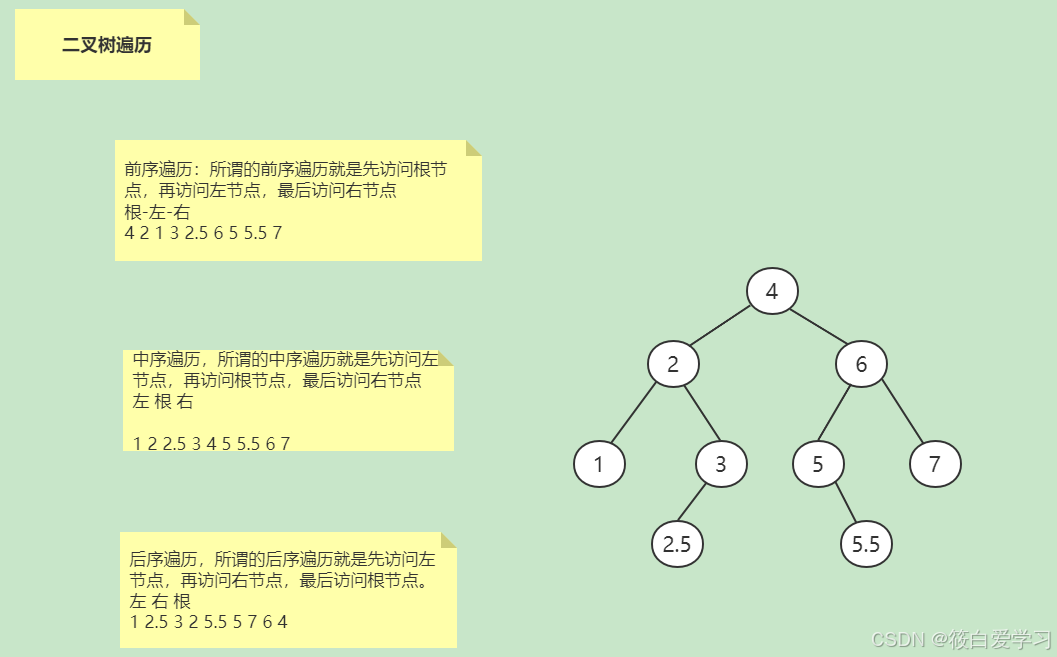
二叉树中的遍历规则有如下三种:
- 中序遍历:所谓的中序遍历就是先访问左节点,再访问根节点,最后访问右节点,即左-根-右遍历
- 先序遍历:所谓的前序遍历就是先访问根节点,再访问左节点,最后访问右节点,即根-左-右遍历(前序)
- 后序遍历:所谓的后序遍历就是先访问左节点,再访问右节点,最后访问根节点。即左-右-根遍历
查找最小值:沿着根节点的左子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最小节点
查找最大值:沿着根节点的右子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最大节点
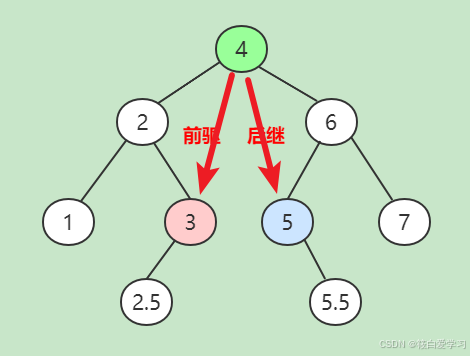
查找前驱节点 :小于当前节点的最大值
查找后继节点 :大于当前节点的最小值
删除节点
二叉树中的删除节点:本质上是找前驱节点或者后继节点来替代
- 叶子节点直接删除
- 只有一个子节点的用子节点替代(本质上就是找的前驱节点或者后继节点,左节点就是前驱节点,右节点就是后继节点)
- 有两个子节点的,需要找到替代节点(替代节点就是前驱节点或者后继节点)
查找局限性
一个二叉查找树是由n个节点随机构成,所以,对于某些情况,二叉查找树会退化成一个有n个节点的线性链.如下图:
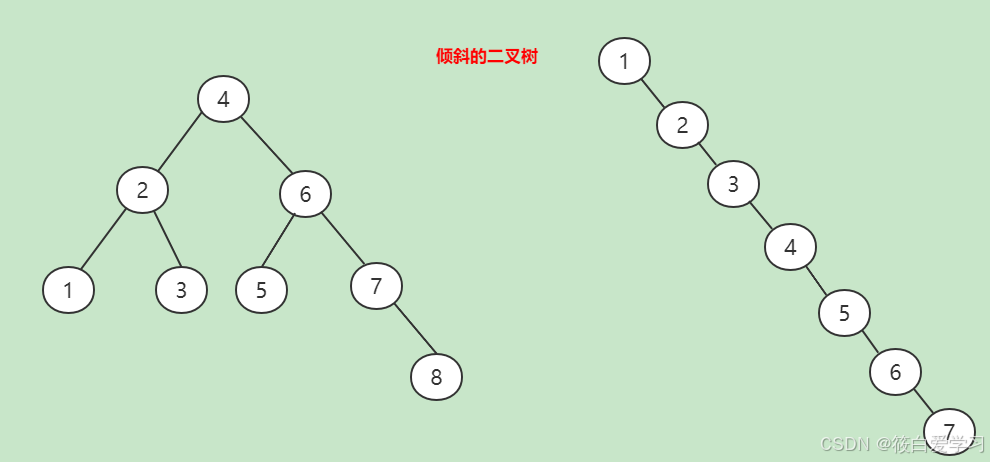
AVL树(高度平衡树)
BST存在的问题是,树在插入的时候会导致倾斜,不同的插入顺序会导致数的高度不一样,而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上,这样树的高度为N。基于BST存在的问题,平衡查找二叉树(Balanced BST)产生了。平衡树的插入和删除的时候,会通过旋转操作将高度保持在LogN。其中两款具有代表性的平衡术分别为AVL树(高度平衡树,具备二叉搜索树的全部特性,而且左右子树高度差不超过1)和红黑树。
AVL树是如何实现平衡的呢?,具体是通过左旋或者右旋来实现的。具体如下图:
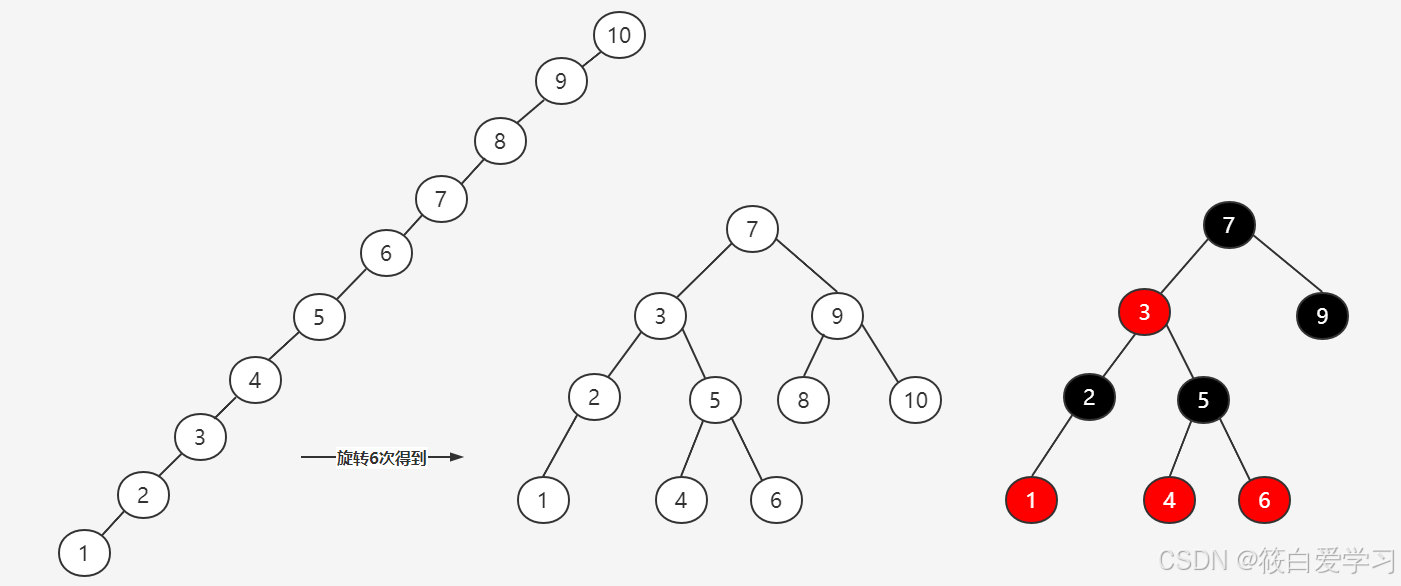
虽然AVL可以解决二叉树所存在的问题,但是AVL树要求太过严格,左旋和右旋的开销会比较大,这时出现了红黑树,只要求黑色节点平衡即可.
2-3-4树
概念介绍
2-3-4树是四阶的 B树(Balance Tree),他属于一种多路查找树,
它的结构有以下限制:
- 所有叶子节点都拥有相同的深度。
- 节点只能是 2-节点、3-节点、4-节点之一。
-
2-节点
-
包含 1 个元素的节点,有 2 个子节点;
-
-
3-节点
-
包含 2 个元素的节点,有 3 个子节点;
-
-
4-节点
-
包含 3 个元素的节点,有 4 个子节点;
-
特性
- 所有节点必须至少包含1个元素
- 元素始终保持排序顺序,整体上保持二叉查找树的性质,即父结点大于左子结点,小于右子结点; 而且结点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下图是一个典型的 2-3-4树
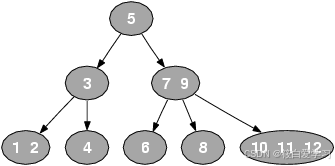
生成的过程
第一次插入---2节点
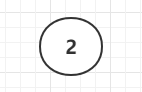
插入第二个节点--3节点 合并
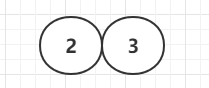
插入第三个节点---4节点 合并
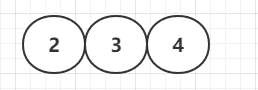
插入第4个节点---需要分裂
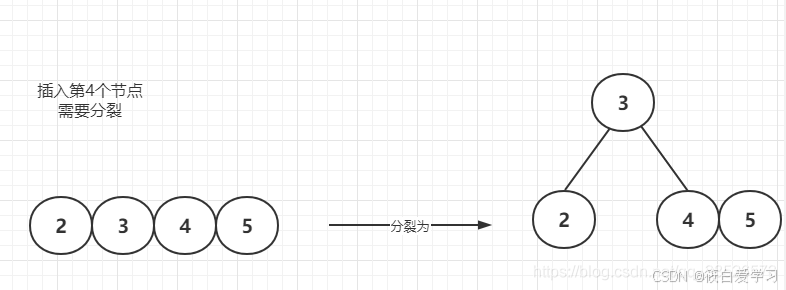
插入6
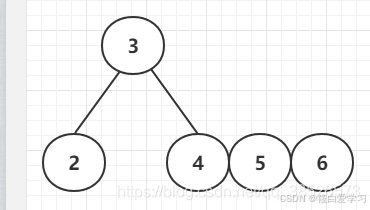
插入7
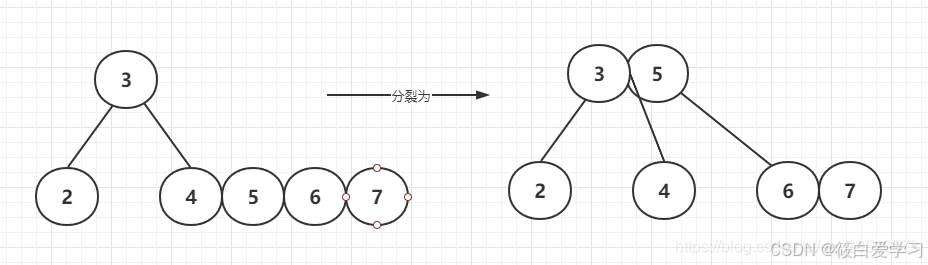
插入8
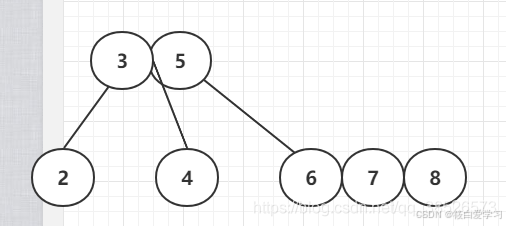
插入9
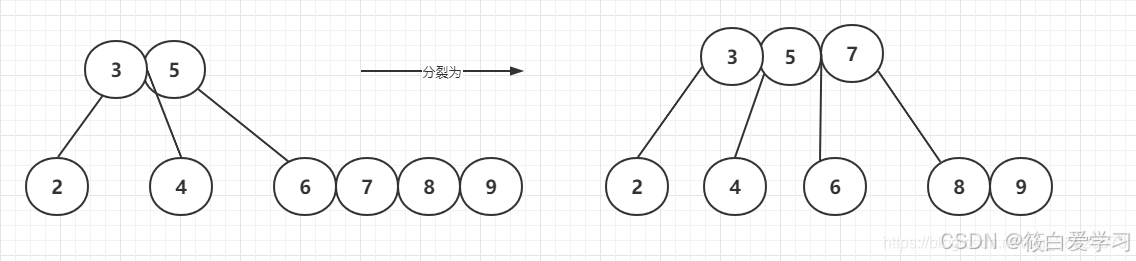
插入10
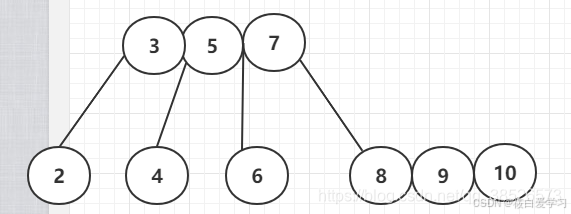
插入11
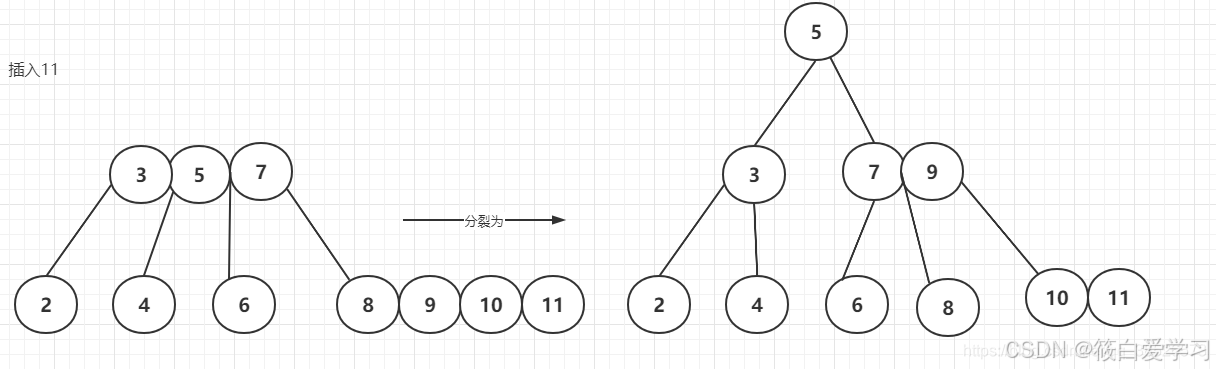
插入12
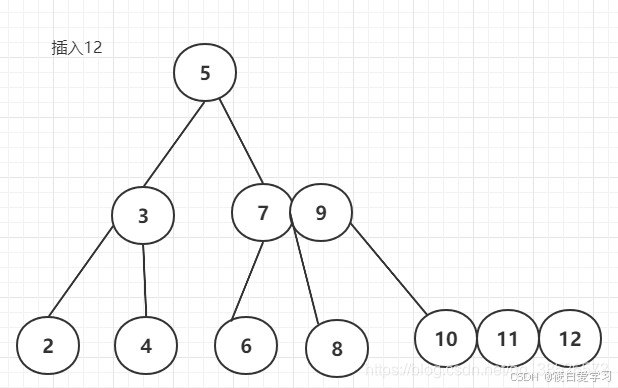
最后插入1来看看效果





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2002
2002

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










