KMP算法

KMP算法作用

KMP算法的作用就是用来解决这道题：可以快速地在原串中找到匹配字符串，haystack是原串，needle是匹配字符串

next数组

next数组简介
KMP算法的核心是next数组，next数组的含义是字符匹配失败时匹配字符串应该回退到哪个字符重新开始匹配，-1就是前面的子串的最长公共前后缀长度（不包括当前字符）
例如第5个字符匹配失败了字符串应该回退到第2个字符重新开始匹配，2-1=1，即前面的子串abea的最长前后缀长度是1
例如匹配字符串abeabf的next数组如下图所示，数组下标从1开始

子串a不能算前后缀，所以next【1】为0
字符串ab没有公共前后缀，所以字符匹配失败后回退到第一个字符a重新开始匹配，next【3】为1
字符串abe没有公共前后缀，所以字符匹配失败后回退到第一个字符a重新开始匹配，next【4】为1
字符串abea最长公共前后缀是a，所以字符匹配失败后回退到第二个字符b重新开始匹配，next【5】为2
字符串abeab最长公共前后缀是ab，所以字符匹配失败后回退到第三个字符e重新开始匹配，next【6】为3

构建next数组
构建next数组是KMP算法的难点，现在我们就来看一下next数组是怎样被构建的,构建next数组的过程有点像dp结合二分，构建next数组就相当于求子串的后缀和前缀是否匹配
子串ab

pre指向前缀的结尾a，suffix指向后缀的结尾b，a和b不相等，prefix没有大于1就不用回退,所以next[3]是1，suffix后移一位，因为后移前是只有一个字符的公共前后缀已经不相等了prefix就不用后移继续往后比较了，suffix后移一位的目的是找一个新的只有一个字符的后缀看是否和只有一个字符的前缀相等

子串abe

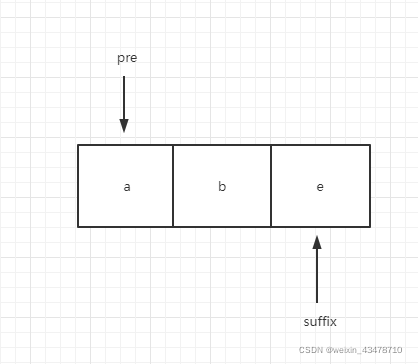
pre指向前缀的结尾a，suffix指向后缀的结尾e，a和e不相等，prefix没有大于1就不用回退,所以next[4]是1，suffix后移一位，

子串abea

pre指向前缀的结尾a，suffix指向后缀的结尾a,a和a相等，最长公共前后缀长度加1，pre和suffix后移一位看所指向的字符是否还相等，相等于在已找到的最长公共前后缀继续匹配，next[5]是2

子串abeab

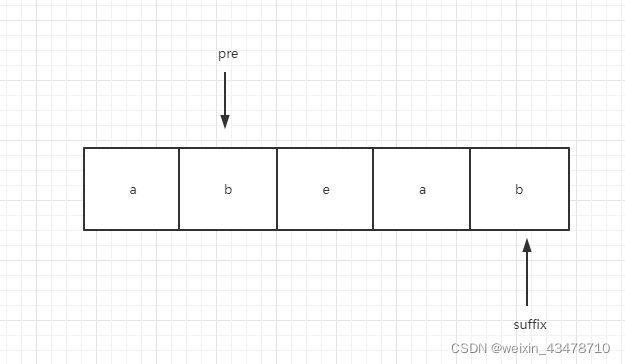
pre指向前缀的结尾b，suffix指向后缀的结尾b,b和b相等,最长公共前后缀长度加1,这步类似于dp，因为当前结果是依靠上一个结果算出来的，pre和suffix后移一位看所指向的字符是否还相等,next[6]是2

子串abeabf
3
pre指向前缀的结尾e，suffix指向后缀的结尾f,e和f不相等，pre就要向前回溯，回溯到前一位的next值继续看是否还有短一点公共前后缀，即next[5],next[5]是3，子串abe没有最长公共前后缀，所以就找不到短一点公共前后缀，next[7]为1,不过next[7]在匹配时是用不上的，因为第7个字符为空，而原串里是没有空字符的，所以是无法匹配的

求next数组匹配失败时回溯的原理：

如图所示next[16]为8表示前15个字符的最长公共前后缀长度是7，即红框部分aaabaaa,两个红框部分是相等的，然后看第8个字符和第16个字符是否匹配，不匹配，就看next[8]是多少，next【8】是4表示前7个字符的最长公共前后缀长度是3，即蓝框部分aaa，因为上一步已经知道了两个红框部分是相等的，即第二个蓝框等于第三个蓝框，又因为第一个蓝框等于第二个蓝框，所以第一个蓝框等于第三个蓝框，即第4个字符和第16个字符匹配前的最长公共前后缀长度是3aaa，然后就看第4个字符和第16个字符是否匹配，匹配了最长公共前后缀长度加1是4，next[17]是5

如果第4个字符和第16个字符不匹配就继续回溯直到回溯的字符和第16个字符匹配或回溯到第一个字符
如果回溯到第一个字符，因为是第一个字符肯定没有公共前后缀，所以直接看第一个字符和第16个字符
是否匹配，不匹配的话next[17]是1，匹配的话next[17]是2

回溯之后的匹配如图所示

回溯的作用就是往前找一个有可能匹配到的最长公共前后缀的位置，继续找第16个字符前面的后缀和第1个字符开始的前缀相等的部分（不包括前一步匹配失败的第9个字符到第15个字符的后缀和第1个字符到第7个字符的前缀），这里是找到的后缀是第13个字符到第15个字符和前缀第1个字符到第3个字符是相等的，这样就能继续匹配第16个字符和第4个字符
例如上面的例子aaabaaac和aaabaaab不匹配，就往前找找到aaab和aaab是否能匹配

一开始是这样匹配的，红框部分，不过匹配失败了,由图可以看出三个蓝框是一样的，所以把下面的字符串右移到第4个字符和上面字符串的第16个字符对齐

KMP算法步骤

有了next数组，就可以开始进行原串和模式匹配串的匹配了


前5个字符都能匹配，第6个字符匹配失败就回退，next[6]为3表示应该回退到第三个字符重新开始匹配

因为红框部分都是相等的，所以红框部分相等于已匹配的，就把匹配字符串右移到下面第一个红框和上面的红框对齐

原串第6个字符和匹配字符串第3个字符匹配失败，next[3]为1表示应该回退到第一个字符重新开始匹配

可以看到从原串第6个字符开始，匹配字符串从第1个字符开始可以全部匹配，所以原串可以和匹配字符串完全匹配的第一个位置是6，原串指针位置-匹配字符串长度

具体代码实现

根据next数组的不同定义可以有两种代码实现

//这种写法next数组表示的时当前子串的最长公共前后缀长度，字符串下标从0开始
public int strStr(String haystack, String needle) {
        char[] chars = haystack.toCharArray();
        char[] chars1 = needle.toCharArray();
        int[] next = new int[chars1.length];
        //计算next数组
        //前缀终止位置-1
        int prefix = 0;
        next[0] = prefix;
        //后缀终止位置-1
        for (int suffix = 1; suffix < next.length ; suffix++) {
            //前后缀末尾不相同的情况，就要向前回溯,直到前后缀结尾一样或prefix为0
            //回溯的位置是前缀结尾的前一位的next数组值
            //例如字符串aaabbab prefix = 2  suffix = 3时不相等时就看prefix的前一位的next数组值，
            //prefix = 1时aa的最长前后缀长度是2，不过前缀aa结尾的a和后缀ab结尾的b不相等还要继续回退
            //prefix = 0可以结束回退，next[3]为0
            //因为prefix的前一位的next数组值记录着prefix的前一位的相同前后缀的长度
            while (prefix > 0 && chars1[prefix] != chars1[suffix]) {
                prefix = next[prefix-1];
            }
            //前后缀末尾相同就继续往后找直到前后缀结尾不一样
            if (chars1[prefix] == chars1[suffix]) {
                prefix++;
            }
            next[suffix] = prefix;
        }
        int b = 0;
        for (int a = 0; a < haystack.length(); a++) {
            //不匹配就回退
            while (b > 0 && chars[a] != chars1[b]) {
                //因为next存的是数组长度，所以这里刚好是回退到已匹配的后一位
                b = next[b-1];
            }
            if (chars[a] == chars1[b]) {
                b++;
            }
            if (b == chars1.length) {
                return a - needle.length() + 1;
            }
        }
        return -1;
    }

//这种写法next数组的含义是当前字符的前面字符的最长公共前后缀长度+1，字符串下标从1开始，下标0为空字符
 public int strStr(String haystack, String needle) {
        if (needle.length() == 0) {
            return 0;
        }
        haystack = " " + haystack;
        needle = " " + needle;
        char[] pattern = needle.toCharArray();
        char[] source = haystack.toCharArray();
        int[] next = new int[pattern.length];
        Arrays.fill(next,1);
        int pre = 1;
        int suffix = 2;
        while (suffix < next.length - 1) {
            while (pre > 1 && pattern[pre] != pattern[suffix]) {
                pre = next[pre];
            }
            if (pattern[pre] == pattern[suffix]) {
                next[++suffix] = ++pre;
                continue;
            }
            suffix++;
        }
        int a = 1, b = 1;
        while (a < source.length) {
            if (source[a] == pattern[b]) {
                a++;
                b++;
                if (b == pattern.length) {
                    return a - pattern.length;
                }
            }
            while (a < source.length && source[a] != pattern[b]) {
                if (b > 1) {
                    b = next[b];
                } else {
                    a++;
                }
            }
        }
        return -1;
    }