AIED 2023: 708-713
作者:Wanyong Feng, Aritra Ghosh, Stephen Sireci, and Andrew S. Lan
其中Aritra Ghosh和Andrew S. Lan是BOBCAT的作者,本篇文章也是对BOBCAT存在的问题(高暴露和覆盖率高)进行了解决。
摘要
CAT是个性化测试的一种形式,它精确地测量学生的知识水平,同时减少测试长度。BOBCAT是最近提出的一个框架,它学习了一个数据驱动的问题选择算法来有效的减少测试长度,并且提高了测试的准确性。然而,它存在高问题暴露和测试覆盖率高的问题,这会潜在的影响测试的安全性。本文介绍了BOBCAT的约束版本,通过改变它的优化设置来解决这些问题,使我们能够权衡测试准确性的问题暴露和测试覆盖率。通过在两个现实世界成人测试数据集上的广泛测试,我们证明了C-BOBCAT是有效的。
1 Introduction
与传统测试/评估机制相比,CAT是一种个性化测试的形式,它基于学生对之前问题的回答适应性的选择下一个问题来有效的减少测试长度。一个CAT系统通常由以下部分构成:一个知识水平估计器,给定之前问题的答案来估计学生当前的知识水平;一个响应模型,给定知识水平估计和问题特征,来预测学生正确回答问题的可能性;和一个问题选择算法,通过给定响应模型的输出,选择下一个最有信息量的问题。尽管CAT已经被广泛的应用到现实世界的测试中已是事实,存在一个重要的局限性,大多数现行的问题选择算法都是静态的,这意味着,随着越来越多的学生通过测试,它不能随着时间的推移得到提升。最近,研究人员们提出了几个关于学习一种数据驱动的问题选择算法的概念性想法。
BOBCAT(和扩展(Fully adaptive framework: neural computerized adaptive testing for online education(2022, 刘淇)))学习了一种数据驱动的问题选择算法,同时支持不同的响应模型。BOBCAT通过解决以下的双层优化问题学习的问题选择算法:内层优化使用问题选择算法选择的问题更新学生的知识水平估计,与此同时,外层优化通过评估对保留数据(即,内部优化没有看到的学生对问题的回答)的最新知识水平估计来更新问题选择算法和响应模型(也就意味着内外层优化的数据集没有交集)。BOBCAT相比于传统的CAT有几个优点:1)BOBCAT通过很少的问题选择就能够达到同样的知识水平估计精度,2)问题选择算法对响应模型是不可知的,这使测试管理者能够探索满足他们需求的最佳组合。
尽管相比于传统的CAT,BOBCAT有几个优势,但是学习到的问题选择算法具有高问题暴露和高测试重叠率的问题。高问题暴露率意味着一些问题不断地被选择,高测试重叠率意味着不同的学生可能得到相近的测试内容。这些局限性可能潜在的影响测试的有效性和公平性,因为邪恶的测试准备活动,集中收集给以前考生的项目(题目)。现行的解决这个问题的方法是为传统CAT设置设计的,通过在问题选择中引入随机性,或者使用最大团算法,不能用于数据驱动的CAT设置。
贡献
在本文中,我们提出了BOBCAT的一个约束版本(C-BOBCAT),它能够权衡问题暴露和测试覆盖率的测试准确性。C-BOBCAT 1)使用了一个随机问题选择算法,而不是确定性的问题选择算法,2)在BOBCAT的优化目标中增加了一个惩罚项,来促进学习到的问题选择算法在不同的学生中选择不同的问题。因此,我们可以通过一个温度超参数来权衡题暴露和测试覆盖率的测试准确性。我们通过在两个现实世界成人测试数据集上的实验,验证了C-BOBCAT的有效性,我们的实现将在以下网站上公开获得:https://github.com/umass-ml4ed/C-BOBCAT。
2 Methodology
我们首先回顾BOBCAT,然后细节讲述C-BOBCAT的框架。
2.1 BOBCAT Bcakground
BOBCAT的目标是解决如下的双层优化问题:
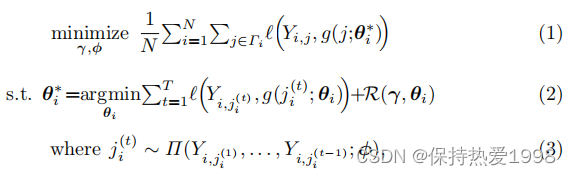
其中,表示参数为
的问题选择算法。输入是某个学生i对之前选择问题的响应(回答)
,输出是要选择的下一个问题的索引
。
表示参数为
的全局响应模型。
包含学生知识水平估计的先验均值和问题难度。输入是学生知识水平估计
和问题id j,输出是学生正确回答问题的可能性。全局响应模型可以是基于IRT的,也可以是基于神经网络的。在一个含有N个学生的batch中,BOBCAT将每个学生i的回答问题分为训练部分
和保留的元部分
。在(2)的内层优化问题中,问题选择算法从
中选择下一个问题。当前学生的知识水平估计为
是对学生知识水平估计的先验均值的局部适应,通过最小化所选问题上的二元交叉熵损失
和防止大偏差的惩罚函数
之和,计算为
和
的函数(这里是
看做是
和
的函数)。在(1)中的外层优化问题中,以当前学生知识水平估计
作为输入,通过最小化保留元数据的二元交叉熵来更新全局响应模型和问题选择算法。对于进一步的细节,参考参考文献【1】BOBCAT。
2.2 C-BOBCAT
我们现在详细介绍对BOBCAT的修改。我们将BOBCAT的潜在问题选择算法从确定性转为随机性,这为每个学生选择的问题注入了一些随机性。具体来说,我们将元是的分类问题选择分布转换为具有固定温度参数的Gumbel-Softmax分布。此外,因为分布的熵随着分布趋于均匀分布而增加,最大化分类问题选择分布的熵可以进一步鼓励学习到的问题选择算法为每个学生选择一组不同的问题。具体来说,我们将(5)中每个学生的所有所选问题的分类问题选择分布熵的负和加到(1)中的外层优化中,从而在(4)中创建新的外层函数。
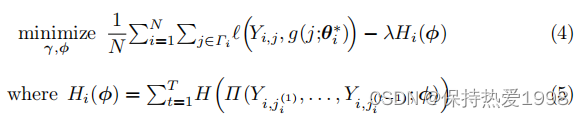
在训练过程中,模型需要最大限度的结合对保留元数据的预测精度和问题选择算法的不确定性,这反映在熵正则化项中。这种平衡通过超参数的值来控制:当
时,问题可简化为元是的BOBCAT双层优化问题;当
时,问题的解决方案是一个用相等的概率来选择每个问题的问题选择算法,即,当问题选择分布为均匀分布时熵最大。在实践中,根据每次测试的需要,测试管理者可以探索
的不同值,来选择一个合适的值,使最大测试准确性与保留可接受的问题暴露和测试重叠率之间达到一个令人满意的平衡。
3. Experiments
我们现在详细介绍我们在两个现实世界成人测试数据集上实施的测试,来验证C-BOBCAT的有效性。
3.1 Data, Experimental Setup, Baseline, and Evaluation Metrics
我们采用来自马萨诸塞州成人能力测试(MAPT)的两个新的公开数据集,阅读理解测试(MAPT-read)和数学测试(MAPT-read)。在两个数据集中,一共有超过90K的学生,1.7K的问题,和4M的问题响应。我们使用这些数据集,因为他们都是从真实测试中收集的,而在原始的BOBCAT论文中使用的数据集是是在学生较长时间的学习过程中收集的。因此,MAPT数据集更接近CAT处理的实际真实情况,也就是说,一个考生的能力在一个短暂的测试中是大致保持不变的。我们选择BOBCAT中基于梯度计算的方法来学习C-BOBCAT框架的问题选择算法(C-BINN-Approx和C-BIIRT-Approx)。我们将学生之间的数据集分别分为训练、验证和测试集,比例分别为6:2:2.对每个学生i,我们将他们回答的问题(以及他们的回答)分为训练部分(,80%)和保留的元部分(
,20%)。我们选择基于IRT的主动学习方法(IRT-Active),和基于IRT的随机问题选择方法(IRT-Random)作为基线模型。我们使用ROC曲线下的面积(AUC)作为指标来评估对保留的元数据
的预测性能。我们使用问题暴露率的比例卡方统计数据(EXPOSE-CHI)(下面全是EXPOSE-PHI,写错了?)和两个学生之间测试重叠率的平均值(OVERLAP-MU)来测量问题暴露率和测试重叠率。
3.2 Results and Discussion
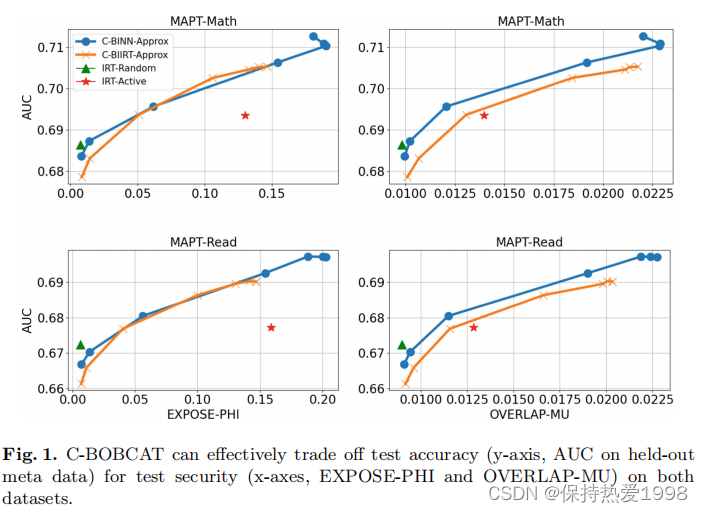
在图1中,我们使用了一系列的图来演示C-BOBCAT如何权衡测试准确性(保留的元数据的AUC)和测试安全性(EXPOSE-PHI和OVERLAP-MU)。对于C-BINN-Approx和C-BIIRT-Approx二者,曲线上的每个点都对应于超参数的一个特定值。基线对应于单个点,因为它们不支持这种权衡。我们观察到,在图的第一列AUC和EXPOSE-PHI呈正相关。当
趋于无穷时,即分类问题选择分布的熵最大时,这两个指标都达到了最小。在这种情况下,问题选择算法等概率的选择每个问题,这就降低了问题的暴露率和测试的准确性。当
趋向于0时,即分类问题选择分布的熵最小时,这两个指标达到最大。在这种情况下,问题选择算法贪婪地选择能够使测试准确性最高的问题,这也导致了较高的问题暴露率。在图的第二列中,OVERLAP-MU和AUC之间也发现了类似的关系。更重要的是,在相同EXPOSE-PHI的和OVERLAP-MU值下,C-BINN-Approx和C-BIIRT-Approx达到了比基线IRT-Active更高的AUC。这一观察结果表明,C-BOBCAT不考虑潜在的反应模型(也是模型不可知的),并且总是比IRT-Active基线在测试准确sing、问题暴露和测试重叠率之间取得更好的平衡。
4 Conclusions and Future Work
在本文中,我们提出了C-BOBCAT,一个试图在CAT设置中的测试准确性和安全性之间取得平衡,我们通过在两个现实世界数据集上的实验证明了它是有效的。未来的工作途经包括 1)研究将问题信息和学生回答相结合作为问题选择算法的新输入的效果;2)对于多项选择问题,研究预测学生选择的确切选项而不是正确性内层和外层水平优化的正确性的效果;3)在实际测试中部署C-BOBCAT。




 本文介绍了一种改进版的BOBCAT框架C-BOBCAT,通过调整优化设置解决高问题暴露和覆盖率问题,旨在提高测试的准确性并平衡问题暴露与测试覆盖。实验证明了C-BOBCAT在成人测试数据集上的有效性。
本文介绍了一种改进版的BOBCAT框架C-BOBCAT,通过调整优化设置解决高问题暴露和覆盖率问题,旨在提高测试的准确性并平衡问题暴露与测试覆盖。实验证明了C-BOBCAT在成人测试数据集上的有效性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








