图论2

一、.Bellman-Ford算法O(NE)
简称Ford（福特）算法，同样是用来计算从一个点到其他所有点的最短路径的算法，也是一种单源最短路径算法。
能够处理存在负边权的情况，但无法处理存在负权回路的情况（下文会有详细说明）。
算法时间复杂度：O(NE)，N是顶点数，E是边数。
算法实现：
设s为起点，dis[v]即为s到v的最短距离，pre[v]为v前驱。w[j]是边j的长度，且j连接u、v。
初始化：dis[s]=0,dis[v]=∞（v≠s），pre[s]=0
For (i = 1; i <= n-1; i++)
For (j = 1; j <= E; j++) //注意要枚举所有边，不能枚举点。
if (dis[u]+w[j]<dis[v]) 　 //u、v分别是这条边连接的两个点。
{
dis[v] =dis[u] + w[j];
pre[v] = u;
}
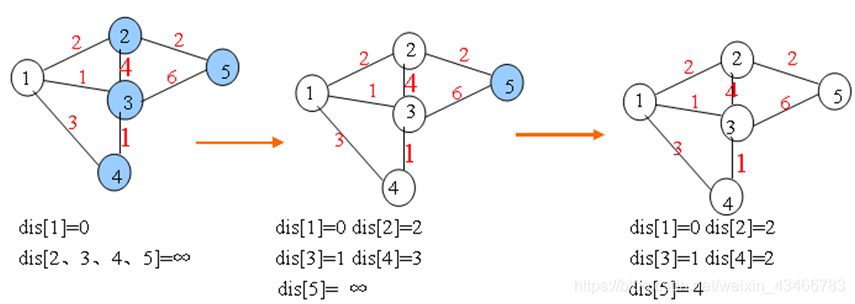
思路：Bellman-Ford算法的思想很简单。一开始认为起点是白点(dis[1]=0)，每一次都枚举所有的边，必然会有一些边，连接着白点和蓝点。因此每次都能用所有的白点去修改所有的蓝点，每次循环也必然会有至少一个蓝点变成白点。

二、SPFA算法O(kE)
SPFA是Bellman-Ford算法的一种队列实现，减少了不必要的冗余计算。
主要思想是：
初始时将起点加入队列。每次从队列中取出一个元素，并对所有与它相邻的点进行修改，若某个相邻的点修改成功，则将其入队。直到队列为空时算法结束。
这个算法，简单的说就是队列优化的bellman-ford，利用了每个点不会更新次数太多的特点发明的此算法。
SPFA 在形式上和广度优先搜索非常类似，不同的是广度优先搜索中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是说一个点修改过其它的点之后，过了一段时间可能会获得更短的路径，于是再次用来修改其它的点，这样反复进行下去。
算法时间复杂度：O(kE)，E是边数。K是常数，平均值为2
算法实现：
dis[i]记录从起点s到i的最短路径，w[i][j]记录连接i，j的边的长度。pre[v]记录前趋。
team[1…n]为队列，头指针head，尾指针tail。
布尔数组exist[1…n]记录一个点是否现在存在在队列中。
初始化：dis[s]=0,dis[v]=∞（v≠s），memset(exist,false,sizeof(exist));
起点入队team[1]=s; head=0; tail=1;exist[s]=true;
do
{
1、头指针向下移一位，取出指向的点u。
2、exist[u]=false;已被取出了队列
3、for与u相连的所有点v //注意不要去枚举所有点，用数组模拟邻接表存储
if (dis[v]>dis[u]+w[u][v])
{
dis[v]=dis[u]+w[u][v];
pre[v]=u;
if (!exist[v]) //队列中不存在v点，v入队。
{//尾指针下移一位，v入队;
exist[v]=true;
}
｝
}
while (head < tail);
循环队列：
　　采用循环队列能够降低队列大小，队列长度只需开到2*n+5即可。例题中的参考程序使用了循环队列。