CPP[数据结构和算法]Day014 树,每个节点3个指针实现无序N叉树的增删改查,strcpy,memcpy,memset

本文介绍了一个使用三个指针实现无序N叉树的增删改查操作的算法，通过一个通用的数据类型设计，使得节点可以灵活地在二叉树、三叉树乃至N叉树间转换。文章详细解释了节点插入、删除的逻辑，并提供了遍历树的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

0x00 基本概念：

0x01 每个节点3个指针实现无序N叉树的增删改查

0x03 附加：strcpy、memcpy和memset之间的区别

0x00 基本概念：

树结构应用广泛，上到应用程序（例如文件系统），下到底层，调度进程，线程，管理硬件都要用到树这种结构。

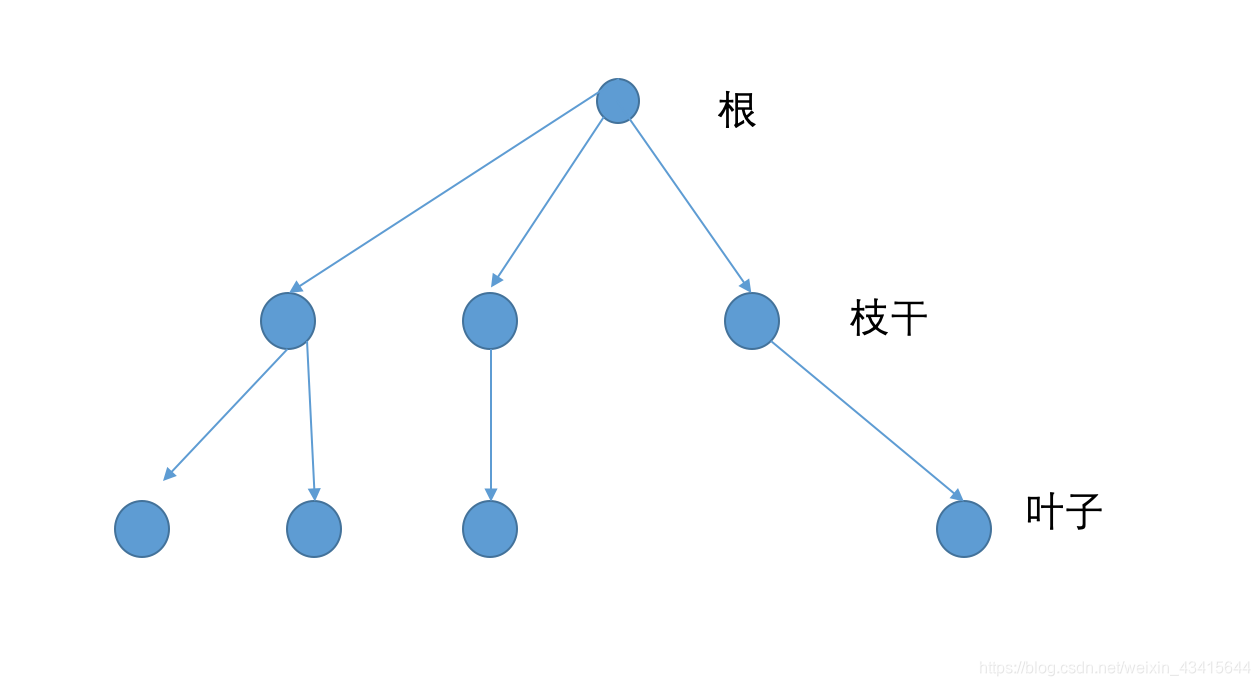
多棵树在一起，且相互有关联，称之为森林

树：一个根，多个分叉
森林：多颗类似的树
节点：树里面每一个元素都是一个节点，也可以单独看成一颗子树
根：第一个节点
层：某些节点到根节点路径长度（箭头个数）如果相同，那么他们在同一层。
路径长度：找到某个节点经过多少次寻址，路径长度就是多少。
高度：距离根节点最远节点的路径长度+1.例如，上面这颗树的高度就是3
N叉树：链表就是一颗一叉树，一棵树最多有多少叉，就是多少叉树。在编程时，首先要将树的节点类型做出来，
孩子节点，父节点，爷爷节点

0x01 每个节点3个指针实现无序N叉树的增删改查

如何设计树的节点类型呢？

By another word，树的节点类型最少需要多少个指针才可以实现随心所欲给树添加节点，想让这颗树成为几叉树就让这颗树成为几叉树呢？

试想假如只有指向孩子的指针，那么2叉树就要两个指针，3叉树就要3个指针。。。。n 叉树就要 n 个指针，而我们需要设计一种通用的数据类型，使得这个节点类型可以组成二叉树，也可以组成三叉树，也可以组成n叉树。

答案是3个指针，一个指针指向父节点，一个指针指向兄弟节点，一个指针指向第一个孩子节点。其中兄弟节点指针便是这个设计的关键，它描述清楚了同层关系。

如上图所示，具有3个指针的节点便描述清楚了一颗任意叉树的所有关系。

无序N叉树的增删改查：

增的思路：首先设置好增加的规则，然后根据规则想好思路，然后实现，然后测试是否存在问题。

遍历的思路：首先设置两个箭头，一个箭头用来向下遍历，一个箭头用来向右遍历，先向右遍历完一层，然后向下遍历一个。

删除的思路：首先指定删除的规则，如果删除的节点pd是孩子（大兄弟），（判断方法：找到删除的节点的父节点，判断父节点的孩子是不是指向被删除的节点，并且它有孩子有兄弟，那么将它的内存释放，然后将pd的孩子归兄弟领养，pd的第一个兄弟成为pd的父的第一个孩子；
如果删除的节点pd是孩子，并且没有兄弟，pd的孩子归父节点领养。

如果删除的节点pd不是孩子，那么让他的孩子认删除节点的大哥为父，让上一个父

如果删除的节点pd没有父，那么pd就是根节点，根节点并不是new出来的，所以不能释放，只能用数据覆盖的方式删除。

#include <iostream>
using namespace std;
#include <cstring> 
template <class T>

//1.制作树的节点类型
class MyTree{
	T data;  //数据 
	MyTree* pParent;//指向父节点的指针 
	MyTree* pBrother;//指向第一个兄弟节点的指针 
	MyTree* pChild;//指向第一个孩子节点的指针 
public:
/*
1.构造函数
2.添加节点
3.删除节点
4.遍历
5.得到节点位置
6.显示数据
*/
//1.构造函数
    MyTree();  
	

    //2.添加节点
    /*
    如何添加节点呢？添加的节点无非是作为调用节点的孩子或者兄弟，
    但是成为第几个孩子，第几个兄弟呢？
    这个比较灵活，需要我们自己来设置添加节点的规则：
	1.新节点如果成为兄弟，那么将成为最小孩子的最小的兄弟
	2.新节点如果成为孩子，那么将成为最小的孩子的孩子 
	*/ 
    void insertNode(const T&data,bool isChild=true); 
    

    //2.删除节点
     /*删除树中某个节点，删除成功，返回true，否则返回false
    如果删除的节点pd是孩子（大兄弟）并且它 有孩子有兄弟
	那么 pd的孩子归兄弟领养，pd的第一个兄弟成为pd的父的第一个孩子；
	如果删除的节点pd是孩子，并且没有兄弟，pd的孩子归父节点领养。 
     */
     bool deleteNode(const T& data);
    

    //3.遍历整个树
    void travel();
    
   //4.根据数值返回对应节点的位置
   MyTree* getNodePos(const T& data); 
    
   //5.显示某个节点的值
   T showData(MyTree* i){
  	  cout<<i->data;
  	}
 
};

//1.构造函数
template<class T>
MyTree<T>::MyTree(){
	data=0;
	pParent=NULL;
	pBrother=NULL;
	pChild=NULL;	
	}
	

//2.添加节点
template<class T>
void MyTree<T>::insertNode(const T&data,bool isChild){//注意函数的缺省参数只能写在函数原型上。
	//1.创建新节点
	MyTree* pNew=new MyTree;
	memset(pNew,0,sizeof(MyTree));
    //将sizeof(MyTree)大小的内存空间全部set 为0，该函数常用来清空结构体和对象。详解见下文
	pNew->data=data; 
	 //2追踪：
     //套路:定义一个临时的指针作为箭头，用循环让这个箭头不断移动，最终指向最小的孩子。
	 MyTree* pTemp= this;//指向当前对象，提防只有一个根节点。
	 while(pTemp->pChild){//如果pTemp有孩子 
	 	pTemp=pTemp->pChild;
	 } //循环之后pTemp就会指向最小的孩子 
	  
	  
	if(isChild){//data要成为最小的孩子 
		pTemp->pChild=pNew;
		pNew->pParent=pTemp; 
		
		
	} else{//成为最小的孩子的最小兄弟 
		//找最小的兄弟
		while(pTemp->pBrother){
			pTemp=pTemp->pBrother;
		}
		pTemp->pBrother=pNew;
		pNew->pParent=pTemp->pParent; 
	}
} 


//3.删除节点
template<class T>
bool MyTree<T>::deleteNode(const T& data){
	//指向要删除的结点 
	MyTree* pDelete=getNodePos(data);
	if(pDelete==NULL) return false;
	//指向要删除的节点的父亲
	MyTree* pDelParent=pDelete->pParent; 
	if(NULL==pDelParent) {//要删除的节点没有父，说明是根节点 
    //根节点不是new出来的，只能用覆盖的方式删除
	  if(pDelete->pBrother){//有兄弟，用兄弟的值来覆盖根节点的值
	     MyTree* pTemp=NULL;
	    //case1:如果要删除的节点的兄弟有孩子，要删除的节点的孩子应该成为它的兄弟的孩子 
	      if(this->pChild){
	      	pDelete->pBrother->pChild=this->pChild;
	      	pTemp=this->pChild;
	      	while(pTemp){//根的兄弟成为根的每一个孩子的父。 
	      		pTemp->pParent=pDelete->pBrother;
	      		pTemp=pTemp->pBrother;
			  }
	      	
		  }  
		  //case2:要删除的节点的兄弟没有孩子 
		  //如果根的兄弟成为根 
		  this->data=this->pBrother->data;
		  this->pChild=pDelete->pBrother->pChild;//万一根也有孩子呢？那岂不是孩子丢了？
	      this->pBrother=pDelete->pBrother->pBrother;
		   
	  	
	  } 
	  else{//根节点没有兄弟 
	    if(this->pChild){//如果根有孩子，用孩子覆盖根 
	    	this->data=this->pChild->data;
	    	//注意顺序 
			this->pBrother=this->pChild->pBrother;
			this->pChild=this->pChild->pChild; 
			 
		} 
		
	}
	return true;
	
}
if(pDelParent->pChild==pDelete){//要删除的节点是老大 
	   if(pDelete->pBrother)//老大有兄弟 
       {
       	//老大的所有孩子的父指针指向老二
       	//判断老大是否有孩子
		  
		  
		  //如果有孩子 
		  if(pDelete->pChild){
		  	pDelete->pChild->pParent=pDelete->pBrother;   
       	    MyTree* temp= pDelete->pChild;
       	
		   while(temp->pBrother){
		   	   temp->pBrother->pParent=pDelete->pBrother;
		   	   temp->pBrother=temp->pBrother->pBrother;
       		
		   }
		   
	    //老大的大儿子成为老二最小的儿子
	    MyTree* Tem=pDelete->pBrother->pChild;
	    while(Tem->pBrother){
	    	Tem=Tem->pBrother;
		}
		
		Tem->pBrother=pDelete->pChild;
		pDelParent->pChild=pDelete->pBrother; 
		  	
		  }
		  else{
		  	//如果没有孩子
		  
		   pDelParent->pChild=pDelete->pBrother; 
		  	
		  }
		
	    
	
       	/*
       	pDelete->data==pDelete->pBrother->data;
       	while(pDelete->pBrother->pBrother){
       		pDelete->pBrother=pDelete->pBrother->pBrother
		   }
		   */
		
		
       
			   }
			   
			   		
	   //老大没有兄弟
	  else{
	  //假设老大有孩子 
	  if(pDelete->pChild) 
	  {
	  	pDelParent->pChild=pDelete->pChild;
	  	
		pDelete->pChild->pParent=pDelParent;   
       	MyTree* temp= pDelete->pChild;
       	
		   while(temp->pBrother){
		   	   temp->pBrother->pParent=pDelParent;
		   	   temp->pBrother=temp->pBrother->pBrother;}
	  	
	  }
	  	
		   	   
	  else{
	  	return true;
	  }
	   
	   
	    
	}
	}
	
	
	else{//要删除的节点不是老大 
	/*定规则，孩子归父亲领养*/
	if(pDelete->pChild){
		MyTree* TEmp=pDelete->pChild;
		 TEmp->pParent=pDelete->pParent; 
		while(TEmp->pBrother){
			TEmp->pBrother->pParent=pDelete->pParent;
			TEmp->pBrother=TEmp->pBrother->pBrother;
		} 
		//假定有比他小的兄弟，且比他小的兄弟有比其小的兄弟
		pDelete->data=pDelete->pBrother->data;
		pDelete->pBrother=pDelete->pBrother->pBrother;//你把比它小的兄弟架空了，万一这个兄弟有孩子呢？握草，好麻烦； 
		
	} 
	else{//没有孩子 
		if(pDelete->pBrother){//咩有孩子但有兄弟 
			pDelete->data=pDelete->pBrother->data;
			if(pDelete->pBrother->pBrother){
				pDelete->pBrother=pDelete->pBrother->pBrother;
			}
			else{
				pDelete->pBrother=NULL; 
			}
		}
		else{ //如果这个节点没有孩子也没有比他小的兄弟，那么如何让比他大的兄弟的指针的指向NULL呢？ 
		}
		
	}
		
		
		
	}
	delete pDelete;
	return true; 
} 



//4.在树中找数据并返回节点首地址，如果找不到，返回NULL 
//抄遍历的写法，稍作修改 
template <class T>
 MyTree<T>* MyTree<T>::getNodePos(const T& data){
 	MyTree* pTempChild=this;//为了把根节点以及根节点的兄弟都打印上。 
	MyTree* pTempBrother=NULL;
//	pTempChild=pChild;
	while(pTempChild){ 
		//往右走
		pTempBrother=pTempChild;
		while(pTempBrother){
			if(pTempBrother->data== data) return pTempBrother;
			pTempBrother=pTempBrother->pBrother;
		} 
		//往下走 
		pTempChild=pTempChild->pChild; 
	} 
	return NULL;
 }


//5.遍历树
template<class T>
void MyTree<T>::travel(){
	MyTree* pTempChild=this;//为了把根节点以及根节点的兄弟都打印上。 
	MyTree* pTempBrother=NULL;
//	pTempChild=pChild;
	while(pTempChild){ 
		//往右走
		pTempBrother=pTempChild;
		while(pTempBrother){
			cout<<pTempBrother->data<<" "; 
			pTempBrother=pTempBrother->pBrother;
		} 
		cout<<endl;
		//往下走 
		pTempChild=pTempChild->pChild; 
	} 
	
}

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int main(int argc, char** argv) {
    MyTree<int> tree;
    tree.insertNode(1);
    tree.insertNode(2,false);
    tree.insertNode(3,false);
    tree.insertNode(11);
    tree.insertNode(13,false);
    tree.insertNode(111);
    tree.insertNode(1111,false);
   	tree.travel();
   	cout<<tree.getNodePos(11)<<endl;
   	if(tree.getNodePos(11))
   	tree.showData(tree.getNodePos(11));
   	else
   	cout<<"not find";
   	cout<<endl;
	
	tree.deleteNode(0);
	tree.travel();
	return 0;
}

0x03 附加：strcpy、memcpy和memset之间的区别

strcpy比较简单，就是拷贝字符串，遇到'\0'时结束拷贝。

memcpy用来做内存拷贝，可以拷贝任何数据类型的对象并指定拷贝数据的长度：char a[100],b[50]; memcpy(b, a, sizeof(b));

总结一下：

strcpy和memcpy主要有以下3方面的区别。
复制的内容不同。strcpy只能复制字符串，而memcpy可以复制任意内容，例如字符数组、整型、结构体、类等。
复制的方法不同。strcpy不需要指定长度，它遇到字符串结束符"\0"便结束。memcpy则是根据其第3个参数决定复制的长度。
用途不同。通常在复制字符串时用strcpy，而需要复制其他类型数据时则一般用memcpy。

//注意：如果用的是sizeof(a),则会造成内存泄露。

比较复杂点的是memset，用来对一段内存空间全部设置为某个字符，一般用在对定义的字符串进行初始化为‘ ’或‘\0’，比如：

char a[100];memset(a, '\0', sizeof(a));

另外比较方便的是对结构体的操作， memset可以方便的清空一个结构类型的变量或数组：

比如有结构体struct sample_strcut stTest，一般清空结构体的话得用如下方式：

struct sample_struct
{
 char   csName[16];
 int    iSeq;
 int    iType;
};


stTest.csName[0]='\0';
stTest.iSeq=0;
stTest.iType=0;

而如果用memset就非常方便了：

memset(&stTest,0,sizeof(struct sample_struct));