算法导论学习笔记8_基本数据结构

---

1. 栈和队列

栈和队列是两个基本的动态集合，其中栈遵循后进先出(LIFO)的原则，队列遵循先进先出(FIFO)的原则。

下图展示了元素入栈出栈的过程：

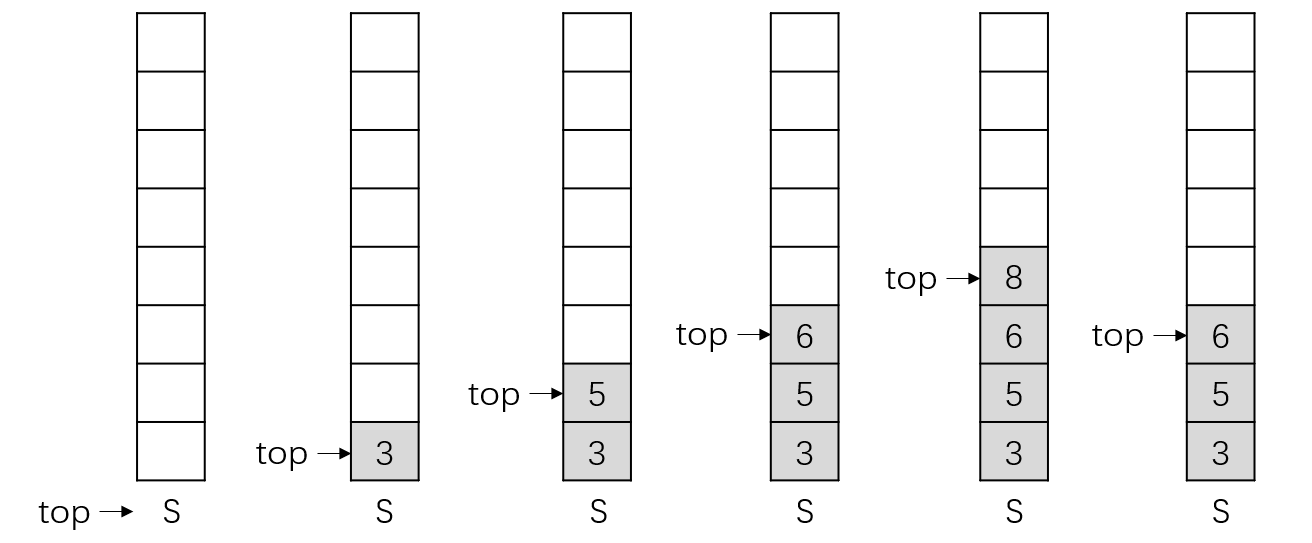
下列是与栈有关的操作：

• stack.push() 将元素压入栈中
• stack.pop() 将栈顶元素弹出
• stack.empty() 判断栈是否为空
• stack.top() 返回栈顶元素

附录中是用数组实现的简单的栈，其中实现了上述了操作。此外，C++的STL库中有现成的栈可供使用。

下图展示了队列的相关操作：

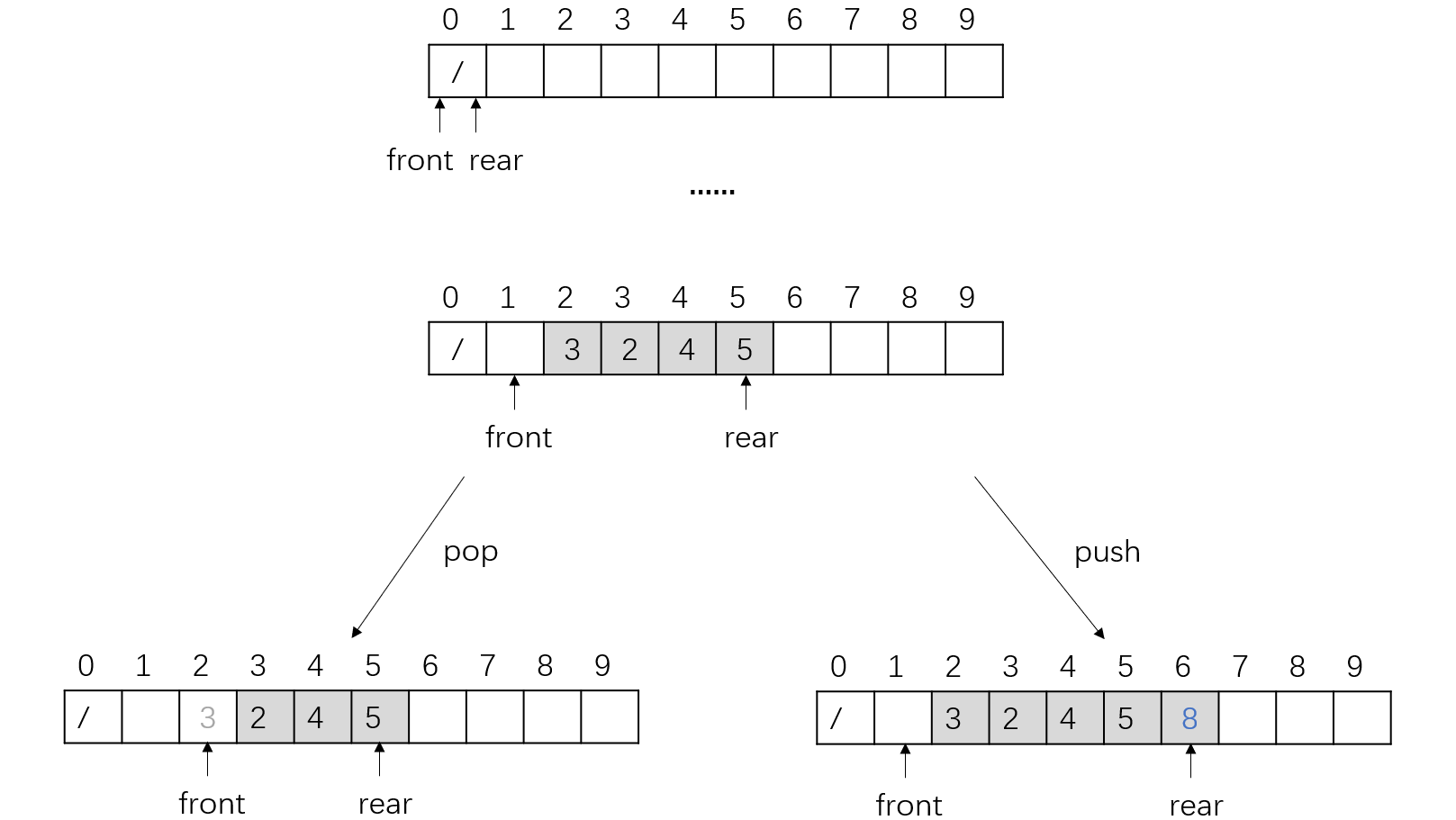
与栈不同的是，队列中有两个辅助变量，分别用于表示队首和队尾的位置。当一个元素入队时，相当于在队伍的末端添加一个元素，因此$rear=rear+1$；当队首元素出队时，相当于队伍最前端的元素离开队伍，因此$front=front+1$。由于随着元素的出入，$front$和$rear$都在不停的增加，因此当队列长度一定时，$front$和$rear$很快就会到达数组尾端，解决这个问题的方法有很多，最常见的就是将其改造为循环队列。

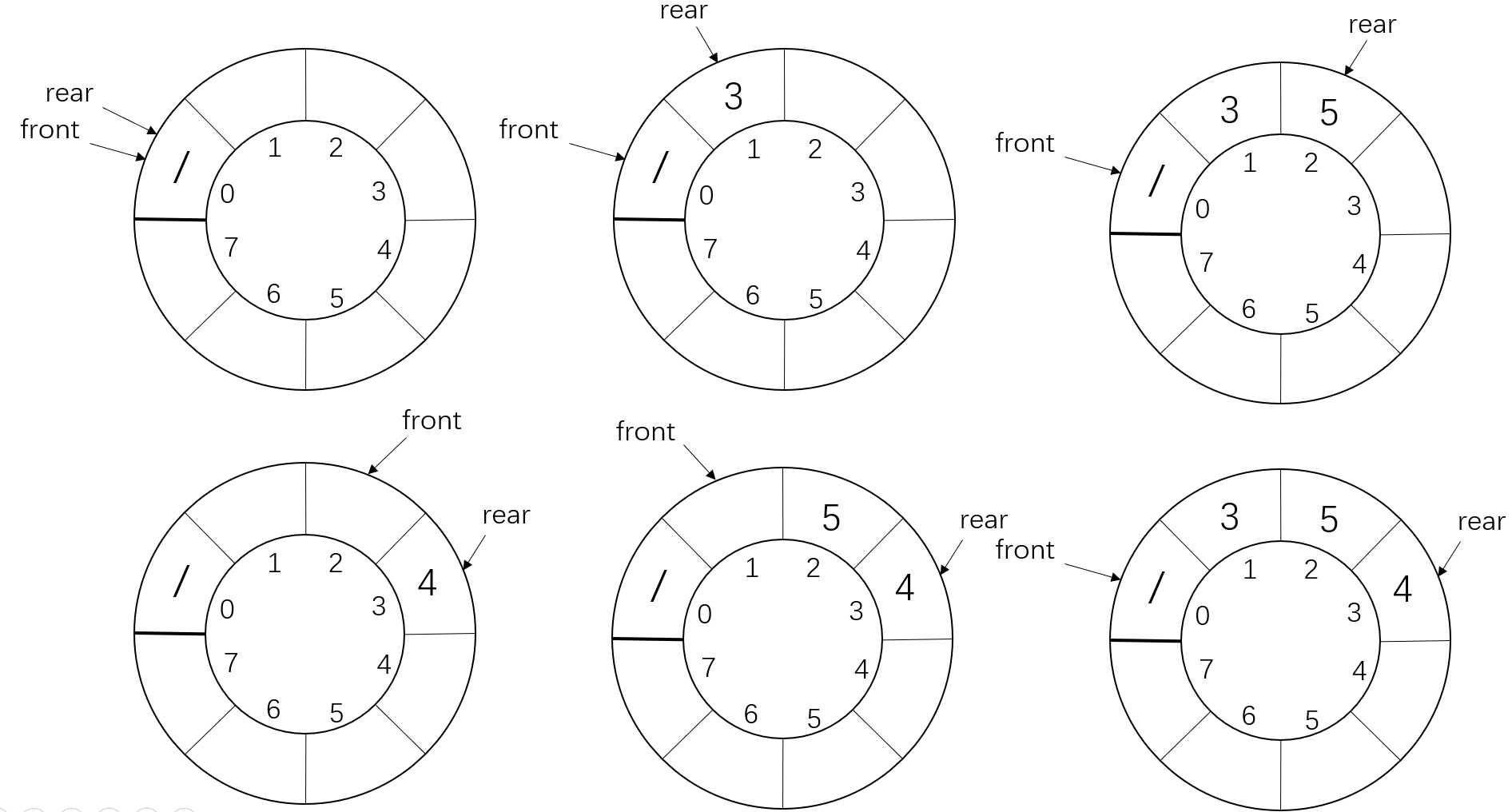
在循环队列中，需要判断队满和队空等状态。当对队伍中所有空间都进行占用时，判断队满和队空时的条件均为$front==rear$。解决这个问题的方法有很多，如对队伍中元素进行计数、设置标志位、牺牲一个元素空间等。

最常用的方法是第三种方法，即牺牲一个元素空间以便于区分队满和队空，因为这种方法不需要额外增加其他变量。于是，判断队空的条件为：$front==rear$，判断队满的条件为：$(rear+1)\%length==front$。

附录中有简单的实现代码。同样的，STL库中也提供了队列的相关对象和操作。

2. 链表

链表是另一个常见的数据结构，它是一种线性表，其中的各个对象按线性顺序排列。与数组不同的是，链表在内存中的存储顺序往往不是顺序的，它通过指针将所有对象链接起来，因此称作链表。常见的链表结构有单向链表、双向链表、循环链表等。

下图是单向链表的结构示意图：

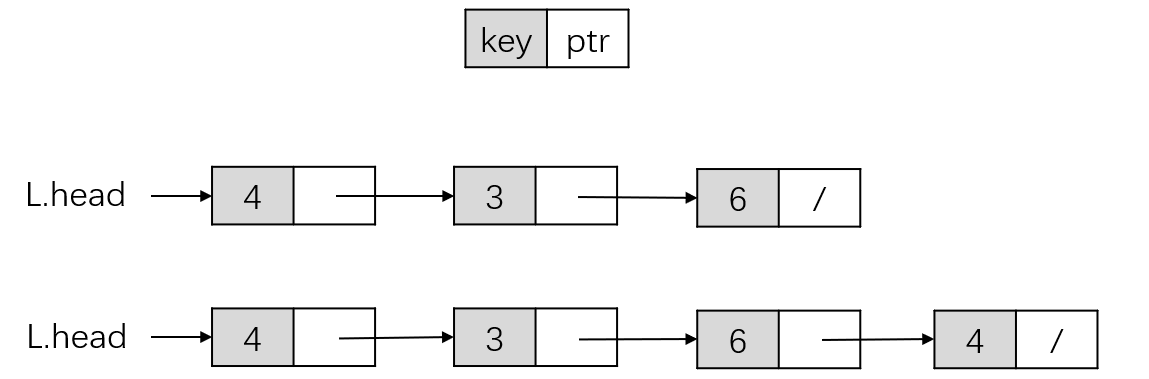
单向链表的结点通常由关键字key、指针域ptr、以及卫星数据构成。这里为了表示链表结构，省略掉了卫星数据。从上图中可以看出，单向链表的指针ptr指向链表的下一个对象，从而将所有的对象串联成一个链式结构。

双向链表的结构如下图所示：

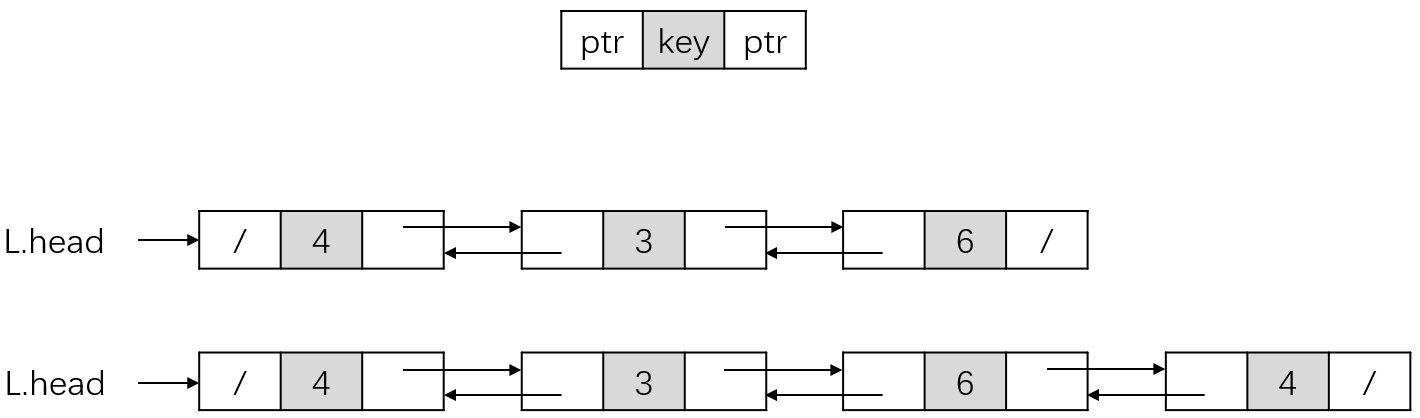
从上图可以看出，双向链表有两个指针域ptr，其中一个指针指向下一个对象，另一个指针指向前一个对象，使得双向链表可以双向迭代。

此外，还有一种较为常用的链表结构–循环链表。下面是一个双向循环链表的结构：

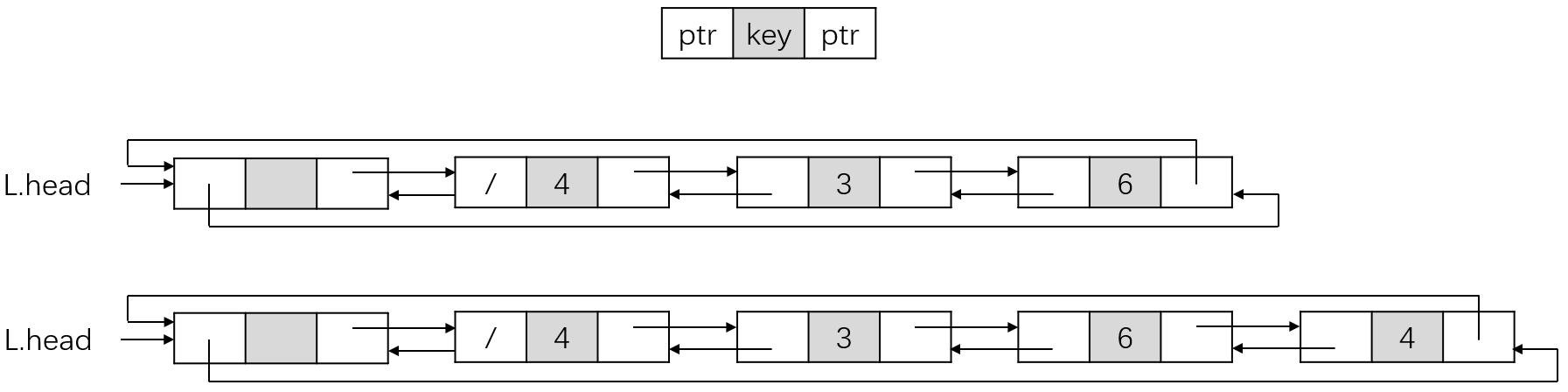
双向循环链表是在双向链表的基础上改进的，将链表中最后一个对象的next指针指向表头对象，将表头对象的prev指针指向表尾对象。此外，为了便于处理边界条件，将表头对象设置为哨兵，它是一个NIL对象，但也和其他对象有相同的属性。

3. 有根树

3.1 二叉树

二叉树是一种最常见的有根树结构，它的结点通常由三个指针域和其他数据构成。其中三个指针域分别为：p、left、right，分别指向该结点的父结点、左孩子结点和右孩子结点。

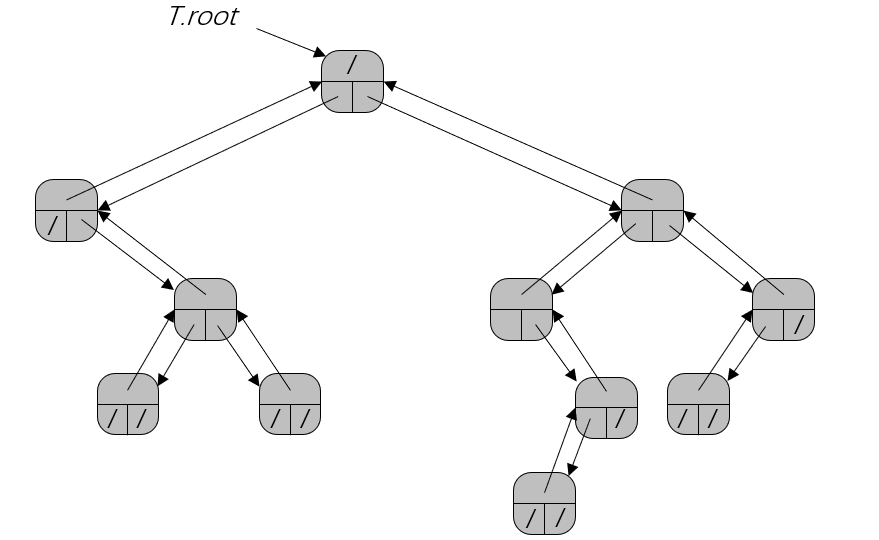
注：属性T.root指向整棵树T的根结点如果T.root=NIL，则该树为空。

3.2 多分支有根树

二叉树的表示方法可以推广到每个结点的孩子树至多为常数k的任意类型的树：只需要将left和right属性用child1，child2,…,childk代替。当孩子的结点数无限制时，这种方法就失效了，因为我们不知道应当余弦分配多少个属性。此外，即是孩子树k限制在一个大的常数以内，但若多数结点只有少量的孩子，则会浪费大量的空间。

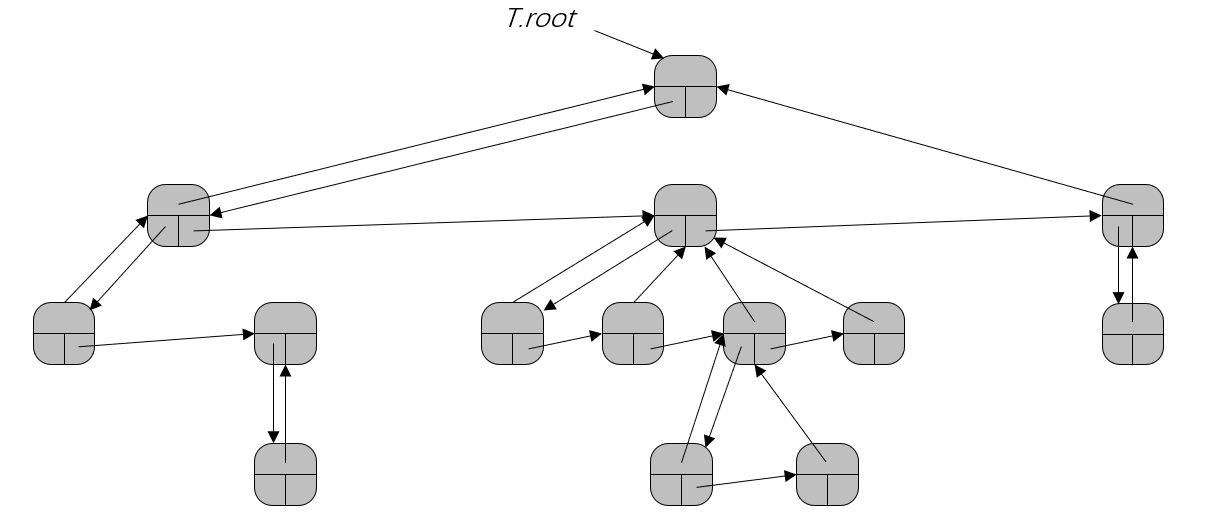
左孩子右兄弟表示法可以用来表示孩子树任意的树。该方法的优势在于，对任意n个结点的有根树，只需要O(n)的存储空间。每个结点都包含一个父结点指针p，且T.root指向树T的根节点，每个结点中不是包含指向每个孩子的指针，而是只有如下两个指针：

• $x.left\_child$：指向结点$x$的最左边的孩子结点。
• $x.right\_sibling$：指向$x$右侧相邻的兄弟结点。

4.附录

4.1 栈代码

#include <iostream>
using namespace std;
class stack {
	int *data;
	int length;
	int pTop = 0;
public:
	stack(int len) :length(len) { data = new int[len+1];};
	~stack() { delete[] data;};
	bool empty();
	void push(int elem);
	void pop();
	int top();
};
bool stack::empty() {
	if (pTop == 0) return true;
	else return false;
}
void stack::push(int elem) {
	if (pTop == length) cout << "stack_overflow!" << endl;
	else data[++pTop] = elem;
}
void stack::pop() {
	if (pTop == 0) cout << "stack_underflow!" << endl;
	else pTop--;
}
int stack::top() {
	if (pTop == 0) {
		cout << "stack_empty!" << endl;
		return 0;
	}
	else return data[pTop];
}
int main(int argc, char* argv[]) {
	stack stack1(10);
	cout << stack1.empty() << endl;
	stack1.push(3);
	stack1.push(5);
	cout << stack1.top() << endl;
	stack1.pop();
	cout << stack1.top() << endl;
	return 1;
}

4.2 队列代码

#include <iostream>
using namespace std;
class queue {
	int *Data;
	int _length = 0;
	int _front = 0;
	int _rear = 0;
	
public:
	queue(int len) :_length(len) { Data = new int[_length]; }
	~queue() { delete[] Data; };
	void push(int elem);
	void pop();
	bool empty();
	int front();
};
void queue::push(int elem) {
	if ((_rear+1)%_length == _front) cout << "queue_overflow" << endl;
	else Data[(++_rear) % _length] = elem;
}
void queue::pop() {
	if (_rear == _front) cout << "queue_underflow" << endl;
	else _front = (_front+1)%_length;
}
bool queue::empty() {
	return _rear == _front;
}
int queue::front() {
	if (_rear == _front) {
		cout << "queue_empty" << endl;
		return -1;
	}
	else return Data[_front+1];
}

int main(int argc, char* argv[]) {
	queue queue1(10);
	cout << queue1.empty() << endl;
	queue1.push(3);
	cout << queue1.empty() << endl;
	queue1.push(4);
	cout << queue1.front() << endl;
	queue1.pop();
	cout << queue1.front() << endl;
	return 1;
}