leetcode Day8----array.easy

Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

找到一串数字的最小值和最大值，并相减得到收益最大。

C语言（1）

int maxProfit(int* prices, int pricesSize) {
    int profit=0;
    for(int i=0;i<pricesSize-1;i++){
        for(int j=i+1;j<pricesSize;j++){
           if(prices[j]-prices[i]>profit){
               profit=prices[j]-prices[i];
           } 
        }
    }
    return profit;
}

Success
Details
Runtime: 792 ms, faster than 21.31% of C online submissions for Best Time to Buy and Sell Stock.
Memory Usage: 7.9 MB, less than 5.17% of C online submissions for Best Time to Buy and Sell Stock.

C语言（2）

正在思考更快的方法，以后更新。。。

python3

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        max_profit, min_price = 0, float('inf')
        for price in prices:
            min_price = min(min_price, price)
            profit = price - min_price
            max_profit = max(max_profit, profit)
        return max_profit
        

Success
Details
Runtime: 52 ms, faster than 30.87% of Python3 online submissions for Best Time to Buy and Sell Stock.
Memory Usage: 13.8 MB, less than 5.08% of Python3 online submissions for Best Time to Buy and Sell Stock.

Best Time to Buy and Sell Stock II

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

对于这道题我开始提交了一份傻瓜式的for循环代码，得到如下结果：

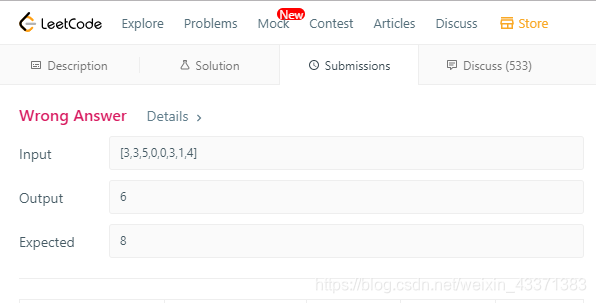
由此可知，并不是限制买两次的（我好傻啊。），所以，改用以下方法：
思路是用temp储存数列中每两个数的差值，如果大于零，则是赚钱的，那么就算进总收益里。

C语言

int maxProfit(int* prices, int pricesSize) {
    int profit = 0;
    for(int i=0;i<pricesSize-1;i++){
        int temp = prices[i+1]-prices[i];
        if(temp>0)
            profit += temp;
    }
    return profit; 
}

Success
Details
Runtime: 4 ms, faster than 87.85% of C online submissions for Best Time to Buy and Sell Stock II.
Memory Usage: 7.9 MB, less than 11.90% of C online submissions for Best Time to Buy and Sell Stock II.

python3

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        profit = 0
        for i in range(len(prices)-1):
            temp=prices[i+1]-prices[i]
            if(temp>0):
                profit+=temp
        return profit
        

Success
Details
Runtime: 52 ms, faster than 22.44% of Python3 online submissions for Best Time to Buy and Sell Stock II.
Memory Usage: 14 MB, less than 5.06% of Python3 online submissions for Best Time to Buy and Sell Stock II.