Codeforces Round #553 (Div. 2) E - Number of Components

题目链接：
http://codeforces.com/contest/1151/problem/E
题意：
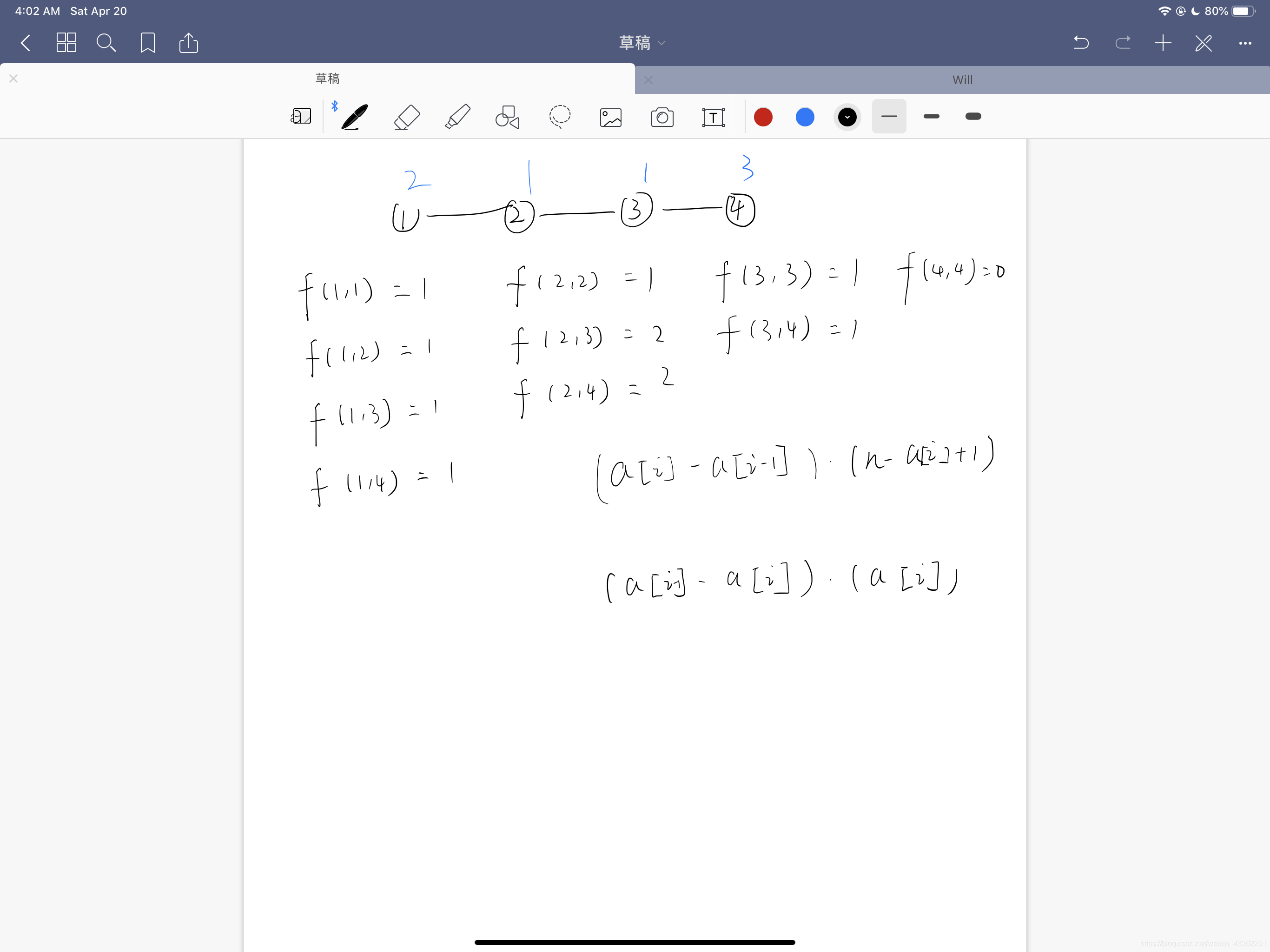
n个点每个点和前一个点以及后一个点相连，且每个点有一个权值。定义一个函数f(l,r)权值在(l,r)的点的联通块的数量。求l从0-n,r从0-n的累加和。
思路：
引用一下出题人的原话

暴力求解很好想，枚举L,R的区间，在每个区间跑一次n循环，开一个新数组b记录权值在范围内的为1,其余为0。来看看不联通的1有几个。
当然这个复杂度是n3，我们可以跑一遍循环。判断相邻的两个点的权值，在多少种L和多少种R的情况下不连通。
如果a[i]>a[i-1]那么对于L要大于a[i-1]小于等于a[i]，对于r要大于等于a[i]小于等于n；所以ans+=(a[i]-a[i-1])(n-a[i]+1)。
如果a[i]<a[i-1]那么对于L要大于0小于等于a[i]，对于r要大于等于a[i]小于等于a[i-1]； 所以ans+=(a[i]-0)(a[i-1]-a[i])。
代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define for1(i,n) for(int i=1;i<=n;i++)
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
const int maxn = 1e5+5;

int a[maxn];

int main(){
    IO;
    int n;cin>>n;
    for1(i,n) cin>>a[i];
    ll ans = 0;
    for1(i,n){
        if(a[i]>a[i-1]) ans+=(a[i]-a[i-1])*1ll*(n-a[i]+1);
        if(a[i]<a[i-1]) ans+=a[i]*1ll*(a[i-1]-a[i]);
    }
    cout << ans<<'\n';
    return 0;
}